Лекция 1. Введение. Основные понятия статики.. Лекции рассматриваются следующие вопросы Введение. Элементы векторной алгебры
 Скачать 299.18 Kb.
|
|
Рис.14 Рис.15 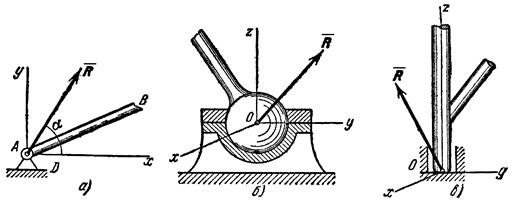 Рис.16 2. Нить (гибкие связи). Связь, осуществленная в виде гибкой нерастяжимой нити (рис.15), не дает телу Мудаляться от точки подвеса нити по направлению AM. Поэтому реакция Тнатянутой нити направлена вдоль нити от тела к точке ее подвеса. Если даже заранее можно догадаться, что реакция направлена к телу, все равно ее надо направить от тела. Таково правило. Оно избавляет от лишних и ненужных предположений и, как убедимся далее, помогает установить сжат стержень или растянут. 3. Цилиндрический шарнир (подшипник). Если два тела соединены болтом, проходящим через отверстия в этих телах, то такое соединение называется шарнирным или просто шарниром; осевая линия болта называется осью шарнира. Тело АВ, прикрепленное шарниром к опоре D (рис.16,а), может поворачиваться как угодно вокруг оси шарнира (в плоскости чертежа); при этом конецА тела не может переместиться ни по какому направлению, перпендикулярному к оси шарнира. Поэтому реакцияR цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной к оси шарнира, т.е. в плоскости Аху. Для силы R в этом случае наперед не известны ни ее модуль R, ни направление (угол  ).4. Шаровой шарнир и подпятник. Этот вид связи закрепляет какую-нибудь точку тела так, что она не может совершать никаких перемещений в пространстве. Примерами таких связей служат шаровая пята, с помощью которой прикрепляется фотоаппарат к штативу (рис.16,б) и подшипник с упором (подпятник) (рис. 16,в). Реакция R шарового шарнира или подпятника может иметь любое направление в пространстве. Для нее наперед неизвестны ни модуль реакции R, ни углы, образуемые ею с осями х, у,z. 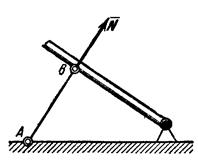 Рис.17 5. Стержень. Пусть в какой-нибудь конструкции связью является стержень АВ, закрепленный на концах шарнирами (рис.17). Примем, что весом стержня по сравнению с воспринимаемой им нагрузкой можно пренебречь. Тогда на стержень будут действовать только две силы приложенные в шарнирах А и В. Но если стержень АВ находится в равновесии, то по аксиоме 1 приложенные в точках А и В силы должны быть направлены вдоль одной прямой, т. е. вдоль оси стержня. Следовательно, нагруженный на концах стержень, весом которого по сравнению с этими нагрузками можно пренебречь, работает только на растяжение или на сжатие. Если такой стержень является связью, то реакция  стержня будет направлена вдоль оси стержня.6. Подвижная шарнирная опора (рис.17.1). Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира. Такая опора не препятствует вращению вокруг оси, но препятствует движению тела в любом направлении в плоскости, перпендикулярной к оси шарнира. Реакция 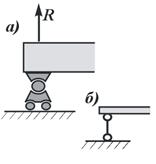 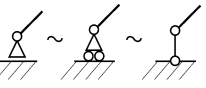такой опоры направлена по нормали к поверхности, на которую опираются катки подвижной опоры. На схемах эту связь изображают так, как показано на рис. 17.1.  Рис.17.1.Шарнирно подвижная опора: а– вид катковой опоры; б – расчетная схема шарнирно-подвижных опор 7. Неподвижная шарнирная опора (рис.18). Реакция R шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие Rx и Ry, соответствующие направлению выбранных осей (рис. 18, а). В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры (рис.18, б) или шарнира (рис 18, в). При решении задач будем реакцию 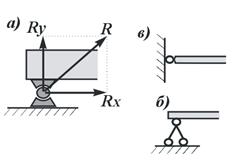 изображать ее составляющими  и  по направлениям осей координат. Если мы, решив задачу, найдем и , то тем самым будет определена и реакция ; по модулю R . Рис.18.Шарнирно-неподвижная опора: а – вид шарнирно-неподвижной опоры; б, в – расчетные схемы шарнирно-неподвижных опор Способ закрепления, показанный на рис.18, употребляется для того, чтобы в балке не возникало дополнительных напряжений при изменении ее длины от изменения температуры или от изгиба. 8. Неподвижная защемляющая опора или жесткая заделка (рис.19, а). Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Балка, изображенная на рис.19, а, жестко заделана в стену в точке А. Перемещению ее в вертикальном направлении, препятствует реакция Ry, перемещению в горизонтальном направлении препятствует реакция Rx и повороту вокруг точки А - опорный момент МА. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Схематическое изображение такой опоры в теоретической механике показано на рис. 1.9, б.Если под такую балку где-нибудь в точке В подвести еще одну опору, то балка станет статически неопределимой. С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.  Рис. 19. Жесткая заделка: а – вид жесткой заделки; б – расчетная схема жесткой заделки При определении реакций связи других конструкций надо установить, разрешает ли она двигаться вдоль трех взаимно перпендикулярных осей и вращаться вокруг этих осей. Если препятствует какому-либо движению – показать соответствующую силу, если препятствует вращению – пару с соответствующим моментом. Иногда приходится исследовать равновесие нетвердых тел. При этом будем пользоваться предположением, что если это нетвердое тело находится в равновесии под действием сил, то его можно рассматривать как твердое тело, используя все правила и методы статики. Связи, как и другие понятия, встречающиеся в аксиомах, являются абстракциями, весьма условно отражающими свойства реальных объектов. Например, рассмотренная выше гибкая невесомая нить может быть моделью подвесных и вантовых систем, у которых масса погонного метра троса составляет десятки и сотни килограммов. Однако усилия, возникающие в таких тросах, во столько раз больше их собственного веса, что при расчете последним можно пренебречь, считая их невесомыми. Пример 1.На невесомую трехшарнирную арку действует горизонтальная сила  (рис.20). Определить линию действия реакции  (реакции связи в точке А).Решение: Рассмотрим правую часть арки отдельно. В точках В и С приложим силы реакции связей 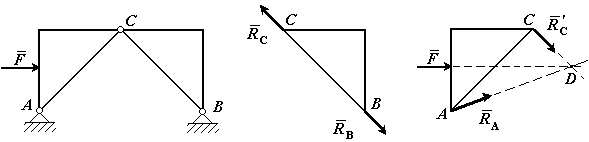  . Тело под действием двух сил находится в равновесии. Согласно аксиоме о равновесии двух сил, силы равны по величине и действуют вдоль одной прямой в противоположные стороны. Таким образом, направление силы нам известно (вдоль линии ВС). Рис.20 Рассмотрим левую часть арки отдельно. В точках А и Сприложим силы реакции связей  . Сила  , действие равно противодействию. На тело действуют три силы, направления двух сил ( и  .) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила направлена вдоль линии AD.Пример 2.Однородный стержень закреплен шарнирно в точке А и опирается на гладкий цилиндр. Определить линию действия реакции 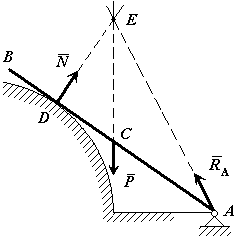(реакции связи в точке А). Рис.21 Решение: Так как стержень однородный, то равнодействующая сил тяжести (сила  ), действующих на стержень, приложена в его геометрическом центре (точка С). Так как стержень опирается на гладкую поверхность, то реакция связи (сила ) в точке касания (точка D) направлена по нормали к этой поверхности. На тело действуют три силы, направления двух сил ( и .) известно. Согласно теореме о трех силах линии действия всех трех сил пресекаются в одной точке. Следовательно, сила направлена вдоль линии AЕ.Пример 3.Найти реакции связей изогнутой балкиАВС, находящейся под действием плоской системы сил (рис.21). Вычисление реакций выполнить при a=1,2 м, b = 2,4 м, l = 1,8 м, α=30°, P1= 8 кН, P2 = 6 кН, М=8 кНм. 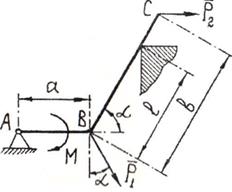  Рис.22 Рис.23 Решение.Освободим балку от связей и приложим к ней реакции связей. На рис.22  - составляющие реакции шарнира А вдоль осей координат  - реакция выступа стены ( перпендикулярноВС).Разложим силы  и на составляющие вдоль осей координат  Условия равновесия балки имеют вид    После решения составленной системы уравнений получаем  Вопросы для самопроверки - В чем состоит предмет статики? - Что такое материальная точка? Система материальных точек? - Что такое абсолютно твердое тело? - Какие величины называются векторными и скалярными? - Что называется моментом силы относительно данной точки и какова его размерность? - Что называется реакциями связей? - Что такое статически эквивалентная система сил? - Что такое аксиомы статики твердого тела? Как они формулируются? - Приведите определение понятия «сила». - Какими приборами измеряют численное значение силы? - Какими единицами измеряется сила в Международной системе (СИ)? - Перечислите признаки, характеризующие силу. - Что называется системой сил? - Приведите примеры сосредоточенных и распределенных сил. - Что называется равнодействующей системы сил? - Какая сила называется уравновешивающей? - Дайте определение внешней и внутренней силы. - Сформулируйте аксиому о равновесии двух сил. - Какие системы сил называются эквивалентными? - Что такое равнодействующая и уравновешивающая сила? - Какие системы сил называются статически эквивалентными? - В чем сходство между равнодействующей и уравновешивающей сил и чем они друг от друга отличаются? - Сформулируйте первую, вторую, третью и четвертую аксиомы статики. - К двум различным точкам твердого тела (см. рис.) приложены две непараллельные, но действующие в одной плоскости силы. Можно ли для сложения этих сил применить правило параллелограмма?  - Можно ли силу в 50 Н разложить на две силы, например, по 200 Н? - Сформулируйте пятую аксиому статики. - Что называют связью? - Какие разновидности связей рассматриваются в статике? - Изменится ли направление реакций связей, если, не меняя положение бруса А, изображенные на рис. а опоры (связи) заменить опорами (связями), как показано на рис. б? (Трение не учитывать, т. е. связи считать идеальными).  - Назовите простейшую систему сил, эквивалентную нулю. - В чем заключается сущность аксиомы присоединения и исключения уравновешивающихся сил? - Назовите сущность аксиомы отвердевания. - Сформулируйте правило параллелограмма сил. - Что выражает аксиома инерции? - Приведите формулировку аксиомы равенства действия и противодействия. - Что называется связью, наложенной на твердое тело? - Что такое реакция связи? - Что называется силой реакции связи? - Сформулируйте принцип освобождаемости от связей. - К какому объекту приложены силы реакций? - Перечислите основные виды связей, для которых заранее известно направление силы реакции. - Назовите связи, для которых заранее известна точка приложения реакции, но не ее направление. - В чем сущность принципа освобождаемости от связей? - Как направлена реакция опорного шарнира, если твердое тело соединено с опорой с помощью стержня, имеющего на концах шарниры? - Почему со стороны неподвижного шарнира на брус действует только сила |