Энг кичик квадратлар усули-fayllar.org. Энг кичик квадратлар усули
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Энг кичик квадратлар усули Энг кичик квадратлар усули.Амалий масалаларда учрайдиган масалаларнинг кўриниши кўпинча мураккаб бўлиб, уларнинг аналитик ифодасини топиш мумкин эмас. Бундай ҳолларда берилган мураккаб функцияни ўрганиш қулайроқ бўлган соддароқ функция билан ёки дифференциал тенгламаларнинг хусусий сонли ечимларга мос келадиган бирорта функция билан алмаштириш мақсадга мувофиқдир. Бунинг учун эркли ўзгарувчи аргемуент билан функциянинг сонли мос қийматлари орасидаги муносабатни функционал боғланишнинг тақрибий ёки аниқ аналитик ифодасини интерполяция формулалари ёки энг кичик квадратлар усули орқали тузиш мумкин. Кўпинча турмушда кузатишлар ва тажрибалар орқали эмпирик формулаларни келтириб чиқариш мумкин. Масалан: ҳароратнинг кўтарилиши ёки аксинча пасайишини, симоб устунининг кўтарилиши ёки пасайишига қараб билиш мумкин. Демак, ҳарорат билан симоб устини ўртасидаги чизиқли боғланиш борлигини тажриба орқали билиш мумкин. Энг кичик квадратлар усули биринчи марта 1874 йилда Гаусс томонидан ишлаб чиқилган бўлиб, айрим адабиётларда бу усул Гаусс усули деб аталади. Энг кичик квадратлар усулининг моҳияти. Тажриба ва амалий масалаларни ечишда берилган маълумотлар асосида уларга мос натажалар олинган бўлсин, яъни Масалан: маълумотлар жадвал кўринишда бўлсин.
Бу қийматларга мос нуқталарни координата текислигида тасвирлайлик. 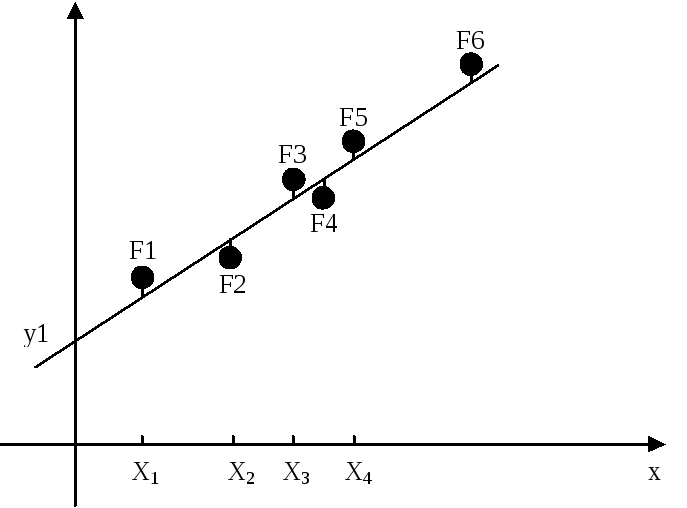 Демак, бу Х ва У ўзгарувчилар орасидаги функционал боғланишни қуйидаги ча белгилаймиз: Масалани ечиш учун биз ана шу тажриба нуқталардан жуда кам фарқ қиладиган Ушбу шарт бажарилиши учун, ноъмалум коэффицентлардан олинган хусусий хосилалар нолга тенг бўлиши керак, яъни 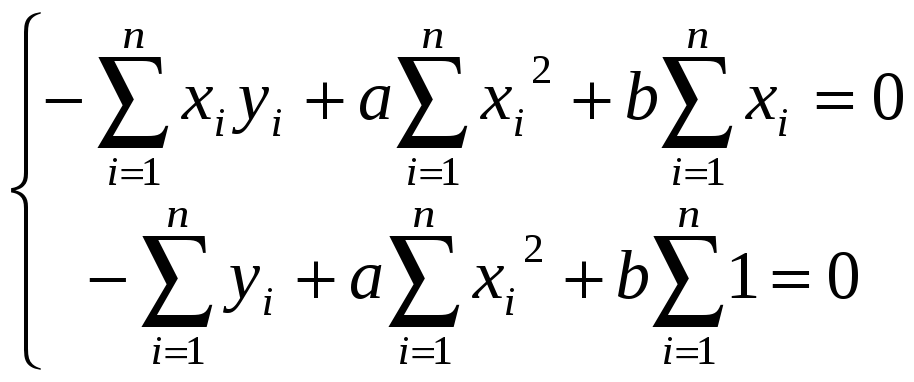 (4) (4) ёки 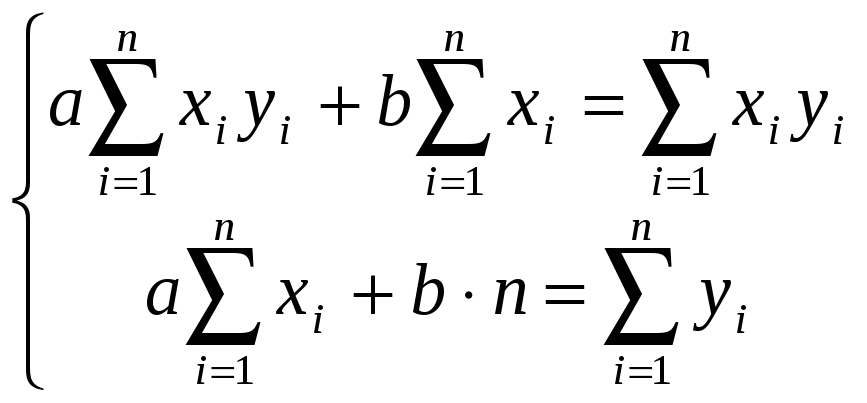 (5) (5) (5) системадан а ва в номаълум коэффицентларни топамиз ва натижада чизиқли функцияни ифодасини ҳосил қиламиз. Масалан: ночизиқли ва параметрик занжирларда сигналларни ўзгартириш. Ночизиқли қаршиликни вольт – ампер тавсифи (ВАТ) жадвалда келтирилган. Шу тавсифни графикда ифодаланг ва уни иккинчи даражали кўпҳад билан аппроксимацияланг.
Квадратлари йиғиндисининг айирмасини функциясини тузамиз: Номаълум коэффицентлардан олинган хусусий хосилалар нолга тенглаймиз: 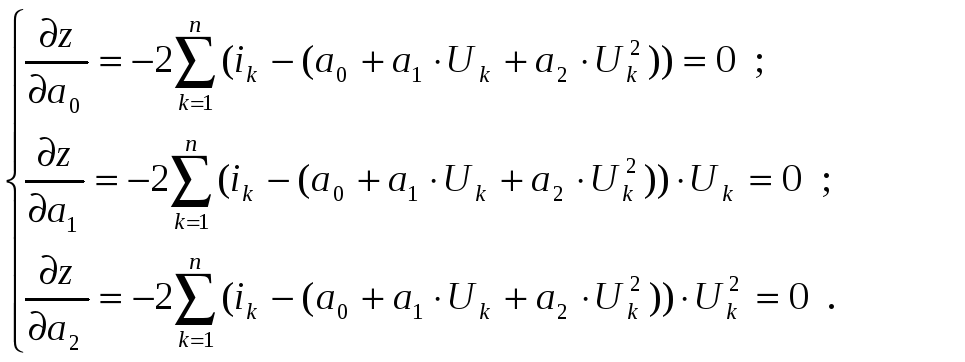 (8) (8) Натижада номаълум коэффициентларга нисбатан тенгламалар системасига келамиз: 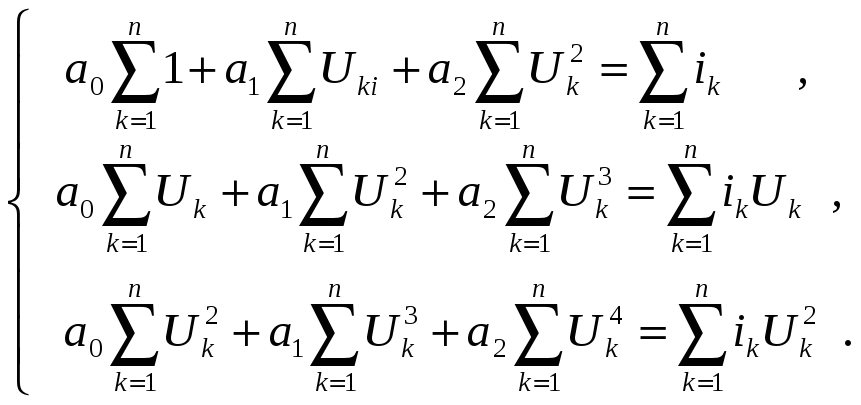 (9) (9) Тенгламалар системасини ечиб, номаълум Функция графигини Maple тилининг икки ўлчовли графикас ёрдамида чизамиз. >plot(0.1+1.03*u+1.15*u^2,u=0..5,color=red); 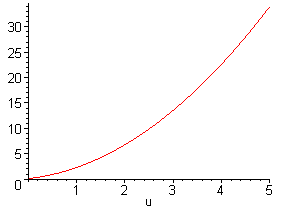 Фойдаланилган адабиётлар рўйҳатиБ.Х.Хўжаёров. Қурилиш масалаларини сонли ечиш усуллари. Тошкент, «Ўзбекистон». 1995 й. Т.Х.Холматов, Н.И.Тойлоқов. Амалий математика, дастурлаш ва компьютернинг дастурий таъминоти. Тошкент. 2000 й. М.И.Исроилов. Ҳисоблаш методлари.Ўзбекистон наширёти, Тошкент 2003й. С.К.Рахмонов. Математик дастурлаш ва оптималлаш усуллари. Маърузалар матни . Фарғона , 2007 й. Т.Дадажонов. Символли ва сонли компьютер матемиатикаси. Maple. Фарғона, 2005 й. В.П.Дьяконов. Спрочник по алгоритам и программам на языке бейсик для персональных ЭВМ. Москва, Наука , 1987г. www.Lib_km.ru www.izcity.com www.softcraft.ru http://fayllar.org |
