Расчет вала при изгибе с кручением (). Еразу
 Скачать 257.68 Kb. Скачать 257.68 Kb.
|
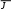 T . (3.2) T . (3.2)p Здесь Mx, My,T – изгибающие и крутящий момент, Jx, Jy – осевые  P моменты инерции, J – полярный момент инерции, x, y– координаты точки, – радиус вектор точки поперечного сечения стержня, в котором определяются напряжения. Используя равенство (3.1), (3.2), можно показать, что в поперечном сечении стержня в виде круга или кольца максимальные значения и находятся по соотношениям:  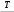 M max W, max 2W, (3.3)  где M Mx My , W – момент сопротивления сечения. Для круга радиуса R D/2 где M Mx My , W – момент сопротивления сечения. Для круга радиуса R D/265 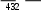 W R3 D3 , (3.4) W R3 D3 , (3.4) 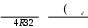 d для кольца, с радиусами r d/2 , R D/2 (c d/ D), W R4 r4 D3 1c4 . (3.5)  В соответствии с третьей теорией прочности должно выполняться условие  2 42 . 2 42 .Подставляя в это неравенство вместо и выражения (3.3) получим |
