Пояснительная записка содержит 17 листов, 5 рисунков, 0 таблиц, 4 использованных источника
 Скачать 280.98 Kb. Скачать 280.98 Kb.
|

Пояснительная записка содержит: 17 листов, 5 рисунков, 0 таблиц, 4 использованных источника. БАЛКА, РЕАКЦИИ СВЯЗЕЙ, СИЛА, МОМЕНТ, УСЛОВИЯ РАВНОВЕСИЯ, ПЛОСКАЯ СИСТЕМА СИЛ, ОСЕВОЙ МОМЕНТ ИНЕРЦИИ, ПОЛЯРНЫЙ МОМЕНТ ИНЕРЦИИ, ОСЕВОЙ МОМЕНТ СОПРОТИВЛЕНИЯ, ПОЛЯРНЫЙ МОМЕНТ СОПРОТИВЛЕНИЯ, ЦЕНТР ТЯЖЕСТИ. Предметом исследования является прочность конструкции. Цель работы – применение общих положений механики деформируемого тела к исследованию прочности. В первой части работы определение реакций связей балки. Во второй части работы определение геометрических характеристик сечения. При оформлении пояснительной записки использовались средства Microsoft-Office. Содержание Введение…………………………………………………………………… Определение реакций опор ………………………………………………. 1.1 Обоснование метода решения…………………………………..…. 1.2 Составление расчетной схемы…………………..………………… 1.3 Аналитическое решение……………………..…………………… Определение геометрических характеристик сечения……………………. 2.1 Обоснование метода решения………………………………….… 2.2 Определение геометрических характеристик сечения ………… Заключение……………………………………………………………… Список использованных источников………………..…………………. Введение Определение реакций опор конструкции Обоснование метода решения Равномерно распределенную нагрузку заменяем сосредоточенной силой, приложенной в геометрическом центре нагруженного участка и имеющей такое же направление. По принципу освобождаемости от связей опора должна быть заменена реакциями связей, препятствующими перемещению точки конструкции, в которой установлена опора. Т.к., конструкция состоит из нескольких твердых тел, соединенных между собой двухсторонними связями, то ее разделяем на части и составляем уравнения равновесия для каждой части отдельно, а затем решаем полученные системы уравнений совместно. Для плоской системы сил условия равновесия могут быть записаны в одной из трех форм: 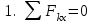 ; ; 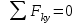 ; ; 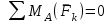 ; ;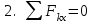 ; ; 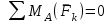 ; ; 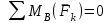 ; ;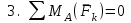 ; ; 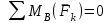 ; ; 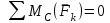 . .Для определения моментов сил относительно точки используется теорема Вариньона: если система сил имеет равнодействующую, то момент этой равнодействующей относительно любой точки равен сумме моментов составляющих относительно этой же точки. Силы, приложенные к балке под углом, отличным от прямого, раскладываем на составляющие, параллельные координатным осям, распределенную нагрузку заменяем сосредоточенной силой Q, приложенной в середине нагруженного участка/ Балка расположена в вертикальной плоскости, жестко защемлена в точке E(рисунок 1.1). 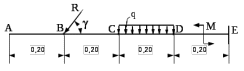 Рисунок 1.1 Схема нагружения балки. На балку действует активные силы: пара сил с моментом M=10 кНм, в точке B на ось действует сосредоточенная сила R=15 кН, на участке CD действует равномерно распределенная нагрузка интенсивности q=10 кН/м. Определить реакции связи в точке Eвызываемые действующими нагрузками. 1.2. Составление расчетной схемы Равномерно распределенную нагрузку, действующую на участке CD, заменим эквивалентной по действию сосредоточенной силой 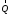 , приложенной в середине нагруженного участка (рисунок 1.1), численно равной , приложенной в середине нагруженного участка (рисунок 1.1), численно равной 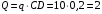 кН, кН,где q=10 Н/м, CD=0,2 м. Проведем координатные оси Azy. Сосредоточенную силу R, действующую под углом к горизонту, спроецируем на оси координат (рисунок 1.2), получим Rz=R*cos(ᵧ)=30*cos(60o)=15 кН, Ry=R*sin(ᵧ)=30*sin(60o)=25.9 кН где R=30 Н,. ᵧ=60o Согласно принципу освобождаемости отбросим жесткую заделку в точке E, заменив её действие реакциями связей 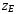 , , 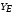 , , 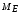 (рисунок 1.2). (рисунок 1.2).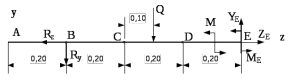 Рисунок 1.2 – Расчетная схема оси колеса. 1.3. Составление уравнений равновесия Для полученной произвольной плоской системы сил составим три уравнения равновесия [1-2] 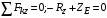 , (1.1) , (1.1)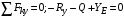 , (1.2) , (1.2)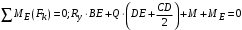 . (1.3) . (1.3)1.4. Определение реакций опор Из уравнения (1.1) ZE=Rz=15 кН, Из уравнения (1.2) YE=Q+Ry=2+26=28кН Из уравнения (1.3) ME=-Ry*BC-Q*(DE+ 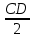 )-M = 26*0.6 – 2*0.3 – 35 = -20 кНм. )-M = 26*0.6 – 2*0.3 – 35 = -20 кНм.Проверка. Составим уравнение моментов относительно точки C 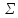 MC(Fk)=Ry*BC – Q* MC(Fk)=Ry*BC – Q*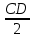 +M+ME+YE*CE= +M+ME+YE*CE=26*0.2 – 2*0.1+35 – 20+28*0.4=0 Т.к. сумма моментов относительно точки C равна нулю, то реакции опор определены верно. Знак минус в ответе говорит о том, что данная реакция направлена противоположно показанной на рисунке 1.2. Определение геометрических характеристик сечения Обоснование метода решения При определении положения центра тяжести сечения необходимо определять значения статических моментов этого сечения. Статическими моментами площади сечения относительно осей 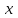 и и 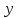 называются определенные интегралы вида: называются определенные интегралы вида: 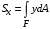 и и 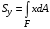 , где F - площадь сечения, , где F - площадь сечения, 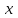 и и 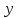 - координаты элемента площади dA. - координаты элемента площади dA.Если известно положение центра тяжести сечения, то статические моменты сечения могут быть подсчитаны по простым формулам, без взятия интегралов, а именно 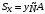 , , 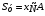 , где , где 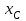 и и 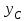 - координаты центра тяжести сечения. - координаты центра тяжести сечения.Оси, проходящие через центр тяжести сечения -называются центральными. Центр тяжести сечения лежит на оси симметрии сечения. Если сечение имеет хотя бы две оси симметрии, то центр тяжести лежит на пересечении этих осей. Для сложного сечения, состоящего из k простейших фигур, координаты центра тяжести сечения определяются по формулам 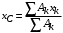 ; ; 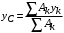 , ,где 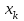 и и 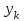 - координаты центров тяжести отдельных фигур сечения, - координаты центров тяжести отдельных фигур сечения, 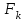 –площадь поперечного сечения k –ой фигуры. –площадь поперечного сечения k –ой фигуры.Моменты инерции сечения тела. Полярным моментом инерции плоской фигуры относительно полюса, лежащего в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных участков на квадраты их расстояний до полюса 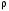 . . 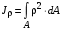 , м4. , м4.Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных участков на квадрат их расстояний до этой оси. 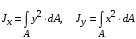 , м4. , м4.Оси, относительно которых моменты инерции имеют максимальные и минимальные значения, называются главными осями инерции. Если главная ось инерции проходит через центр тяжести фигуры, то она называется главной центральной осью, а момент инерции относительно этой оси – главным центральным моментом инерции. Моменты сопротивления сечения тела. Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию от оси до наиболее удаленной точки поперечного сечения 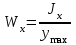 , , 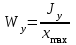 . .Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения 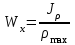 . .В качестве полюса принимается центр тяжести поперечного сечения стержня. Определение геометрических характеристик сечения Делим плоскую фигуру на части, для которых известны или легко определяются площади Ai и координаты центров тяжести xi и yi. В данном случае разобьем сечение на три части (1 – прямоугольник, 2 – треугольник, и 3 –полукруг) (рисунок 2.1).  Рисунок 2.1. Введем обозначения сторон: b1 =30 мм, h=45мм. b2 =45мм, R=15 мм Площадь первой фигуры (прямоугольник) A1=b1*h=30*45=1350i i2 Площадь второй фигуры (треугольник) А2= 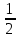 b2*h= b2*h=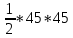 =2025i i2 =2025i i2Площадь третьей фигуры (половина круга), вырезанной из прямоугольника, считаем отрицательной A3=- 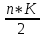 = - = -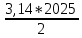 = -824i i2 = -824i i2A= 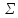 A1=A1+A2+A3=1350+2025-1145=1865мм2 A1=A1+A2+A3=1350+2025-1145=1865мм2Координаты центров тяжести каждой фигуры (рисунке 2.2) x1= 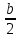 = =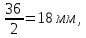 x2=b1+ x2=b1+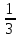 b2=49.6vv b2=30+ b2=49.6vv b2=30+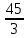 =43.5мм =43.5мм= X3= 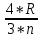 = =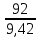 =10,4 мм =10,4 ммy1 = 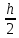 = =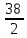 =18 мм, y2 = =18 мм, y2 =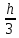 = =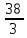 =12,67 мм y3 = =12,67 мм y3 =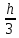 = =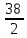 =18 мм =18 мм Рисунок 2.2. Вычисляем координаты центра тяжести плоской фигуры: XN= 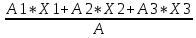 = =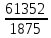 =43.4мм =43.4ммYС = 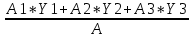 = =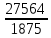 = 19.6мм = 19.6ммЦентр тяжести площади указан на рисунке 2.3. Проводим через центр тяжести главные центральные оси XY и, применяя метод разбиения, находим моменты инерции сечения относительно центральных осей 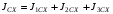 , , 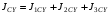 . .Применяя формулы моментов инерции прямоугольника, треугольника и полукруга относительно собственных центральных осей, а также теорему о моменте инерции относительно оси, параллельной центральной (теорему Гюйгенса- Штейнера), записываем.  Рисунок 2.3. Относительно оси X. Прямоугольник J1CX=( 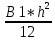 +A1*d12)= +A1*d12)=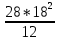 +1254*(4*3)2=1.624*105мм4 +1254*(4*3)2=1.624*105мм4где d1=y1-yC=23.5-18.6=5.7мм Треугольник J2CX=( 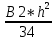 +A2*d22)= +A2*d22)=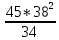 +980*(2.4)2=12.356*104 мv. +980*(2.4)2=12.356*104 мv.D2=y1-yC=18.4-12.7=6.1мм Полукруг J3CX=-( 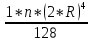 +A3*d3)=-( +A3*d3)=-(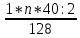 ) +628= -6486*104 мм ) +628= -6486*104 ммгде : D3=y1-yC=18.4-11.7=65.4мм то: JCX=J1CX+J2CX+J3CX=1.624*105+12.356*104 -6886*104=2.857*105 Относительно оси Y. Прямоугольник J1Cy=( 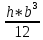 +A1*K1)= +A1*K1)=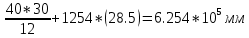 где K1=Xc-X1=43.5-17.3=26.2мм Треугольник J2Cy=( 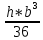 +A1*K22)= +A1*K22)=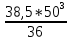 +1154*8.92=2.452*105мм4 +1154*8.92=2.452*105мм4где K2=X2-Xс=54,6 -43,5=11,1мм Полукруг J3Cy=( 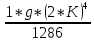 +A3*K32)= +A3*K32)=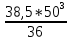 -854*24.3^2=-11.02*105мм4 -854*24.3^2=-11.02*105мм4где K3=XС-X3=54,6 -34,7=19,9мм Т.о., JCX=J1CR+J2CR+J3CR=1.624*105+12.356*104 -6.88*105=4.529*105 Полярный момент инерции плоской фигуры относительно полюса Jp=JCX+JCY =1.624*105+6.356*105=7.487*10 Осевые моменты сопротивления сечения WCX= 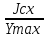 = =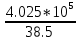 =10.249*103мм =10.249*103ммгде Ymax=h-Yc=40-18.3=26.4мм WCR= 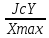 = =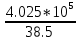 =8.249*103мм =8.249*103ммгде 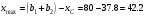 мм. мм.Xmax=(b1+b2)-Xc=83-40.8=36.7мм Полярный момент сопротивления сечения Wp= 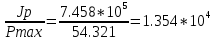 где Pmax= 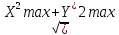 =52.454мм =52.454ммЗаключение В ходе выполнения работы определены реакции опор составной конструкции, определены геометрические характеристики сечения балки. Список литературы Т.В. Хураева. Прикладная механика. Методические указания. Ч.1. – Пенза: Изд-во ПГУ, 2002.– 43 с. Техническая механика. А.А. Эрдеди и др. – М.: Высш. шк., 1980. Сборник задач по технической механике. В. И. Сетков – М.: Высш. шк., 1982. Степин П. А. Сопротивление материалов – М.: Высш. шк., 1979. |
