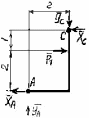
Курсовая работа по теоретической механике. Крикун И. Д. ЭСЭУ, 2 курс, 1 задание. Статика. Определение реакций опор составной конструкции (система двух тел)
 Скачать 58.74 Kb. Скачать 58.74 Kb.
|
|
Министерство транспорта Российской Федерации Федеральное агентство морского и речного транспорта ФГБОУ ВО «ГУМРФ имени адмирала С. О. Макарова» КАФЕДРА ОСНОВ ИНЖЕНЕРНОГО ПРОЕКТИРОВАНИЯ
(Название темы задания) Вариант _________27____________________ (номер варианта) Выполнил студент группы 25.05.06 2 курс (номер группы) Крикун Иван Дмитриевич (Ф. И. О.) Принял преподаватель Потехина Е. В. (Ф. И. О.) «____»________________ 20____ г. Санкт-Петербург 2021 г. Задача №1 Определение реакции опор составной конструкции (система двух тел). Конструкция состоит из двух частей. Определить реакции внешних связей составной конструкции, и реакцию соединительного шарнира С. 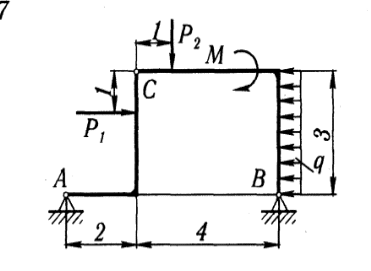
Равномерно распределённую нагрузку q, заменим равнодействующей Q: Q = q*3 Q = 1*3 = 3 кН Составим уравнения проекций сил на оси x и y, а также уравнение моментов относительно точки А: ΣFAix = -XA + P1 - XC = 0 ΣFAiy = YA - YC ∙ 2 = 0 Момент силы относительно точки А: ΣМiA = -YC ∙ 2 + P1 - XC ∙ 3 = 0 XA + XC = 10 кН YA - YC = 0 кН YC ∙ 2 + XC ∙ 3 = 10 кН Рассмотрим равновесие механической системы, расположенной правее шарнира С: 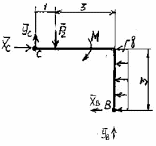 Составим уравнения равновесия механической системы: ΣFBix = Q - XC - XB = 0 ΣFBiy = -P2 - YC + YB = 0 ΣМiB = -XC ∙ 3 – YC ∙ 4 + P2 ∙ 3 – M + Q ∙ 1,5 = 0 -XC + XB = -3 кН YB + YC = 7 кН XC ∙ 3 + YC ∙ 4 = 21 - 11 + 4.5 = 14,5 кН Составим систему уравнений: 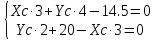 XC ∙ 3 = 14,5 - 4 ∙ YC YC ∙ 2 - (14,5 - 4 ∙ YC) = -20 YC = (-20 + 14,5)/6 = -0,917 кН XC = (14,5 - 4 ∙ (-0,917))/3 = 6,056 кН XA = -XC + P1 = -6,056 + 10 = 3,944 кН YA = YC = -0,917 кН XB = XC - 3 = 6,056 - 3 = 3,056 кН YB = -YC + 7 = 0,917 + 7 = 7,917 кН Полученные реакции в результате расчётов: 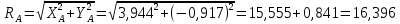 кН кН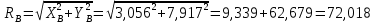 кН кН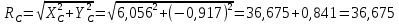 кН кНВыполним проверку: ΣМiB = -XC ∙ 3 – YC ∙ 4 + P2 ∙ 3 – M + Q ∙ 1,5 = = -6,056 ∙ 3 + 0,917 ∙ 4 + 7 ∙ 3 - 11 + 4,5 = 0 Ответ: RC = 36,675 кН RB = 72,018 кН RA = 16,396 кН |