МАТЕША. Если все элементы некоторого столбца или некоторой

• Название: Если все элементы некоторого столбца или некоторой
• Анкор: Matema
• Дата: 12.05.2022
• Размер: 69.44 Kb.
• Имя файла: МАТЕША.docx
• Тип: Документы; #525665

1. 
   Если все элементы некоторого столбца определителя равны нулю, то определитель равен
   

Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).

2. 
   Найти произведение матриц .
   

C=

3. 
   Обратная матрица к матрице 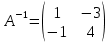имеет вид
   

4. Интеграл сводится к табличному с помощью следующей подстановки

5. Если точки принадлежат прямой , то векторы являются

Коллинеарными
6. Даны векторы Найти вектор

5i-9j+3k
8. Прямые 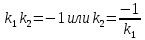и перпендикулярны, если имеет место соотношение


9. Расстояние между плоскостями и равно

2
10. Уравнения асимптот гиперболы имеют вид


11. Плоскость проходит через точку и пересекает ось абсцисс в точке , ось аппликат в точке . Уравнение этой плоскости имеет вид

4x+3y-6z+12=0
12. Вычислить предел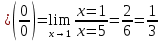



13. Вычислить предел 14. Найти область определения функции

x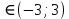

15. Если функция дифференцируема на и для , то функция на

Возрастает
16. Если то



17. Найти промежутки возрастания функции

Промежуток возрастания [-1;0) и [1;+∞)
19. Если функция дифференцируема на и при , то называется для

Первообразной
20. Найти интеграл

21. Вычислить

1
22. Если соответствующие элементы двух столбцов определителя пропорциональны, то определитель

равен нулю
23. Найти произведение матриц



24. Обратная матрица к матрице имеет вид:


25. Интеграл сводится к табличному с помощью следующей подстановки

26. Векторы коллинеарны, если равно

2
27. Скалярное произведение векторов равно

-5

28. Если две прямые и перпендикулярны, то их угловые коэффициенты удовлетворяют соотношению


29. Расстояние между прямыми и равно


30. Даны фокус параболы и уравнение директрисы Уравнение параболы имеет вид

у^2=-28х

31. Прямая перпендикулярна плоскости если соответственно равны

l=2 n=1
32. Вычислить предел

3

33. Вычислить предел


34. Найти область определения функции

Область определения [1,5]
35. Если функция дифференцируема на и для , то функция на

убывает

36. Если то равна


37. Найти экстремумы функции

максимальное значение
39. Дифференцируемая на функция называется первообразной для на , если

для всех х из этого промежутка справедливо равенство
40. Найти неопределенный интеграл

41. Вычислить



42. Вычислить



43. Если определитель имеет два одинаковых столбца, то он равен

Нулю
44. Найти произведение матриц

45. Обратная матрица к матрице имеет вид:


46. Интеграл сводится к табличному с помощью следующей подстановки

47. Если векторы коллинеарны, то их координаты удовлетворяют соотношениям


48. Даны векторы Найти вектор

(3;5;-2) или 3i+5j-2k
49. Если плоскости и перпендикулярны, то их коэффициенты удовлетворяют соотношению

A1A2+B1B2+C1C2=0
50. Плоскости и параллельны, если соответственно равны

m=4 n= -1
51. Большая ось эллипса равна 10, а расстояние между фокусами равно 8. Уравнение эллипса имеет вид


52. Острый угол между прямой и плоскостью равен


53. Вычислить предел =

54. Вычислить предел = 0

55. Найти область определения функции

область определения [-2;2]

56. Если для то функция на

на графике функции выпуклый

57. Найти производную функции


58. Найти промежутки убывания функции

функция убывает в промежутке [0;4]
59. Для функции , заданной на , совокупность всех её первообразных называется

неопределенным интегралом от функции

60. Найти