Ответы(ful)l. Это все, что мне прислали
 Скачать 15.84 Mb. Скачать 15.84 Mb.
|
|
Риск социального ущерба (социальный риск) характеризует масштаб ка- тастрофичности аварии на потенциально опасном объекте. Социальный риск принято представлять математическим ожиданием людских потерь – кол- лективным риском R(Ус), либо плотностью распределения потерь, в интер- претации В. Маршалла [113] F/N – диаграммой, описывающей зависимость час- тоты реализации неблагоприятных событий F, в результате которых погибло не менее N человек, от этого количества человек. Социальный риск учитывает масштаб воздействия, выражающийся в ле- тальных исходах и поражениях людей различной тяжести, приведенных к сум- марно эквивалентному числу летальных исходов. При определении потерь обще- ства от возможных смертельных исходов R(Уc) человеческая жизнь должна оце- ниваться в стоимостном выражении. В качестве такой величины используется цена спасения жизни (ЦСЖ), для обоснования которой в настоящее время при- меняется, по крайней мере, пять подходов с последующим сопоставлением по- лученных значений. В обобщенном виде ЦСЖ понимается как средневзвешенная по наиболее значимым и рисковым областям и сферам жизнедеятельности вели- чина затрат для дополнительного спасения жизни каждого следующего индиви- дуума. Цена спасения жизни относится к разряду тех величин, которые принци- пиально не могут быть вычислены с большой точностью. Поэтому, учитывая значительную неопределенность данной величины, предлагается при расчетах брать несколько уровней значения ЦСЖ – нижнее, среднее и верхнее значения, соответственно 100 тыс., 600 тыс. и 1 млн. руб. на человека [82]. Введенные нами количественные показатели ЦСЖ подтверждаются и установившейся в послед- ние годы практикой выплаты семьям погибших в авариях, катастрофах и экстре- мальных ситуациях 61)Математическая модель потенциального риска.  66) Основные величины, входящие в математическую модель коллективного риска токсического поражения.  N-кол-во людей
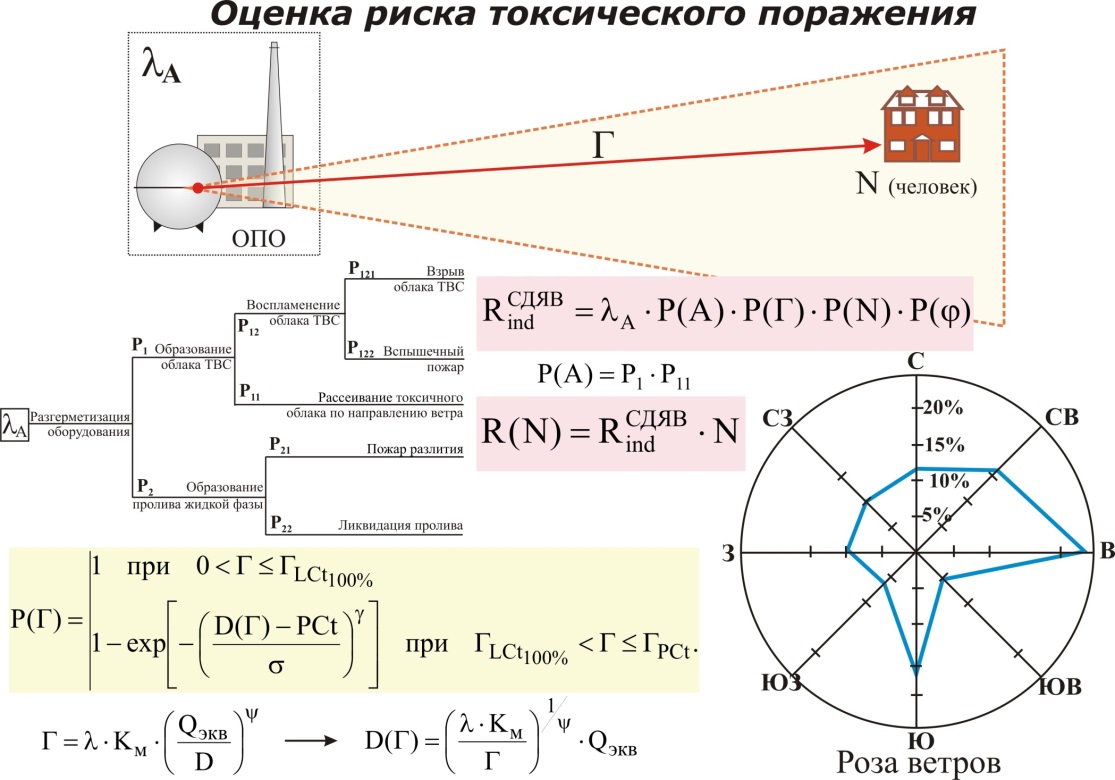
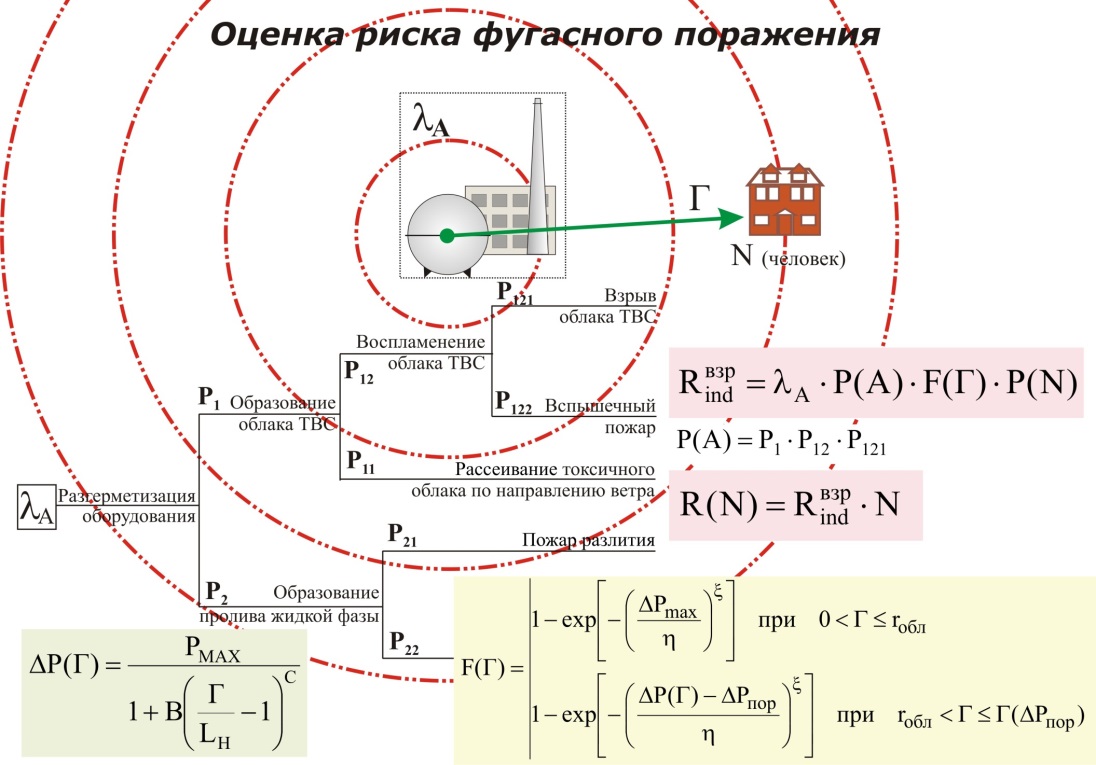
R(N)=Rind*N  N-кол-во людей

модели параметрического ПАРАМЕТРИЧЕСКИЙ ЗАКОН ПОРАЖЕНИЯ Вероятность поражения реципиента в рассматриваемой точке территории Р(Г) описывается распределением Вейбулла, которое принято называть параметрическим законом поражения реципиента.  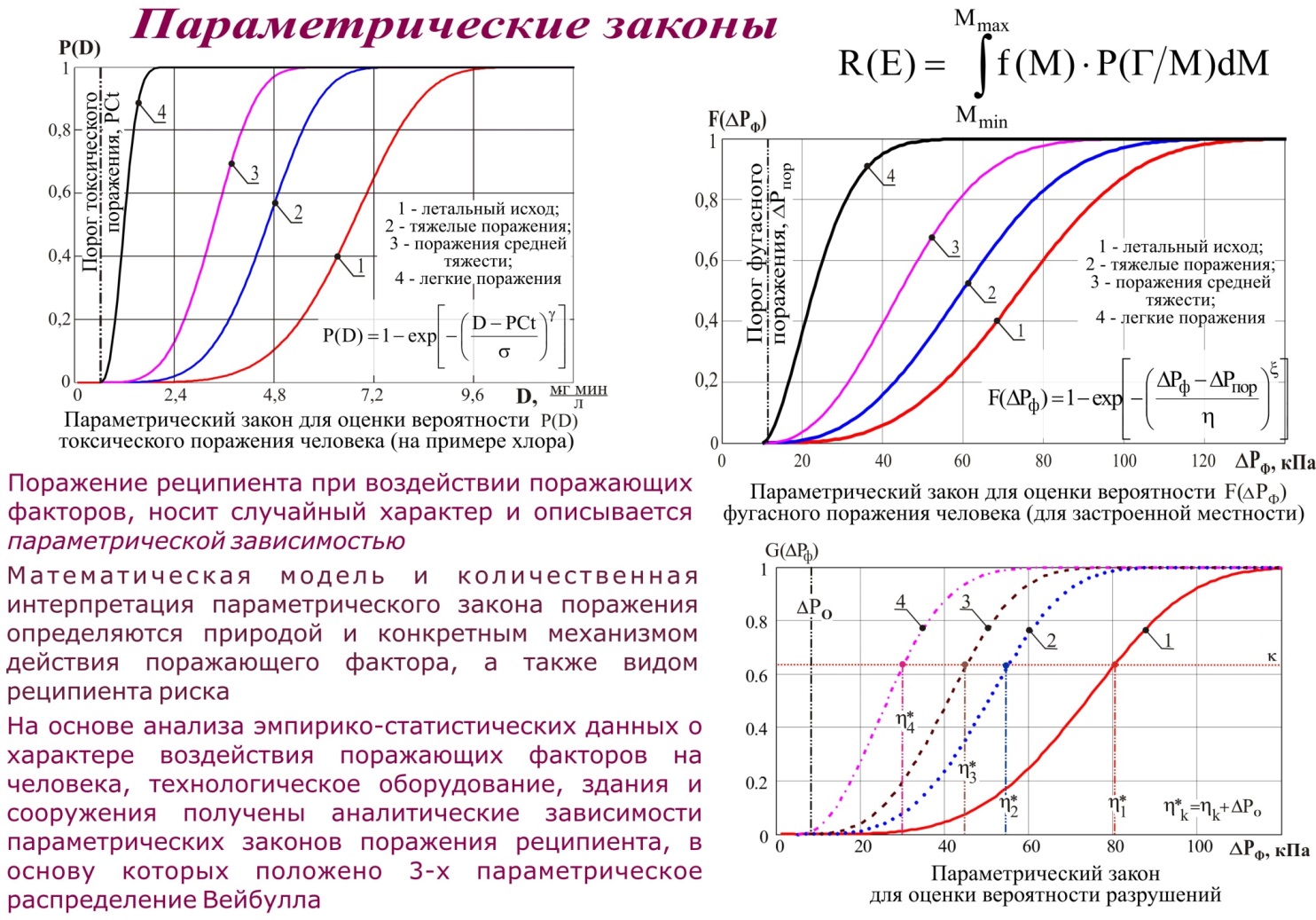 КООРДИНАТНЫЙ ЗАКОН ПОРАЖЕНИЯ Зная параметрический закон поражения человека Р(D), мы не можем судить о характере распределения потенциального риска на прилегающей территории. Для решения данной задачи необходимо знать, как изменяется вероятность поражения человека по мере удаления от источника опасности, то есть от параметрического закона необходимо прейти к координатному закону поражения человека Р(Г).  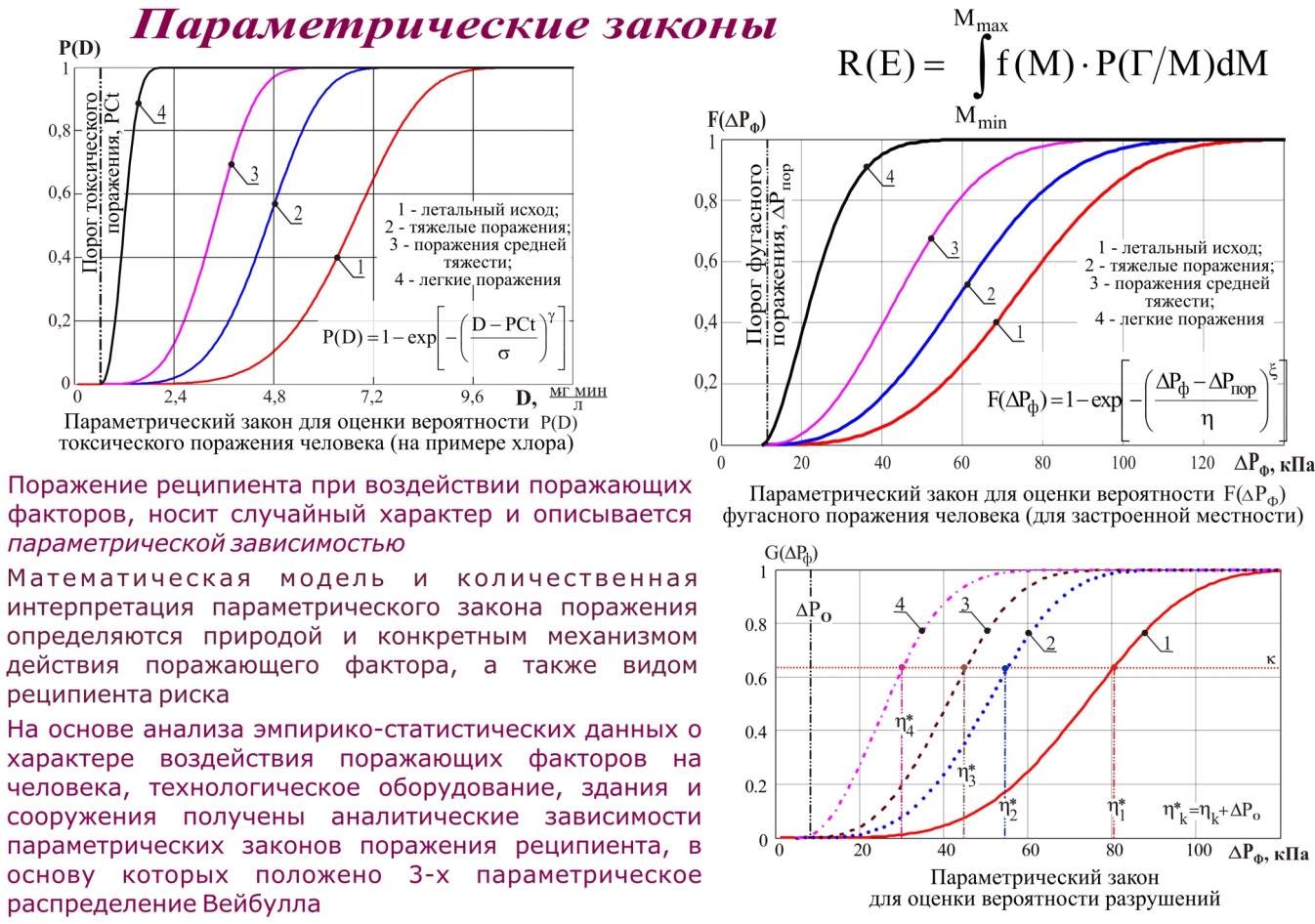
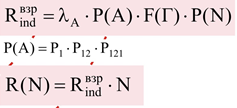
ИНДИВИДУАЛЬНЫЙ РИСК Основные величины, входящие в математическую модель индивидуального риска. По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск Rind = R(E)P(N) Индивидуальный риск – частота поражения отдельного индивидуума (человека) в результате воздействия поражающего фактора. Потенциальный риск на прилегающей к ОПО территории в пределах КВП не может быть равен нулю по определению, в то время как индивидуальный риск может изменяться от нуля до величины потенциального риска (0 ≤ Rиндивидуум ≤ Rпотенциал)
По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск Rind = R(E)P(N)
 N-кол-во людей


R(N)=Rind*N  N-кол-во людей

модели параметрического ПАРАМЕТРИЧЕСКИЙ ЗАКОН ПОРАЖЕНИЯ Вероятность поражения реципиента в рассматриваемой точке территории Р(Г) описывается распределением Вейбулла, которое принято называть параметрическим законом поражения реципиента.   КООРДИНАТНЫЙ ЗАКОН ПОРАЖЕНИЯ Зная параметрический закон поражения человека Р(D), мы не можем судить о характере распределения потенциального риска на прилегающей территории. Для решения данной задачи необходимо знать, как изменяется вероятность поражения человека по мере удаления от источника опасности, то есть от параметрического закона необходимо прейти к координатному закону поражения человека Р(Г).  
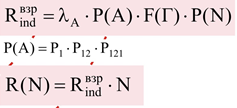
ИНДИВИДУАЛЬНЫЙ РИСК Основные величины, входящие в математическую модель индивидуального риска. По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск Rind = R(E)P(N) Индивидуальный риск – частота поражения отдельного индивидуума (человека) в результате воздействия поражающего фактора. Потенциальный риск на прилегающей к ОПО территории в пределах КВП не может быть равен нулю по определению, в то время как индивидуальный риск может изменяться от нуля до величины потенциального риска (0 ≤ Rиндивидуум ≤ Rпотенциал)
По величине потенциального риска и вероятности нахождения индивидуума в данной точки рассматриваемой территории рассчитывается индивидуальный риск Rind = R(E)P(N) |
