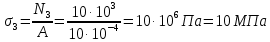Амбарников А.В.,задача. Факультет экологии и инжиниринга
 Скачать 7.02 Mb. Скачать 7.02 Mb.
|
 Задачи по дисциплине: «Прикладная механика» Вариант №3 21.03.01 «Нефтегазовое дело» (ЭОТОНП)
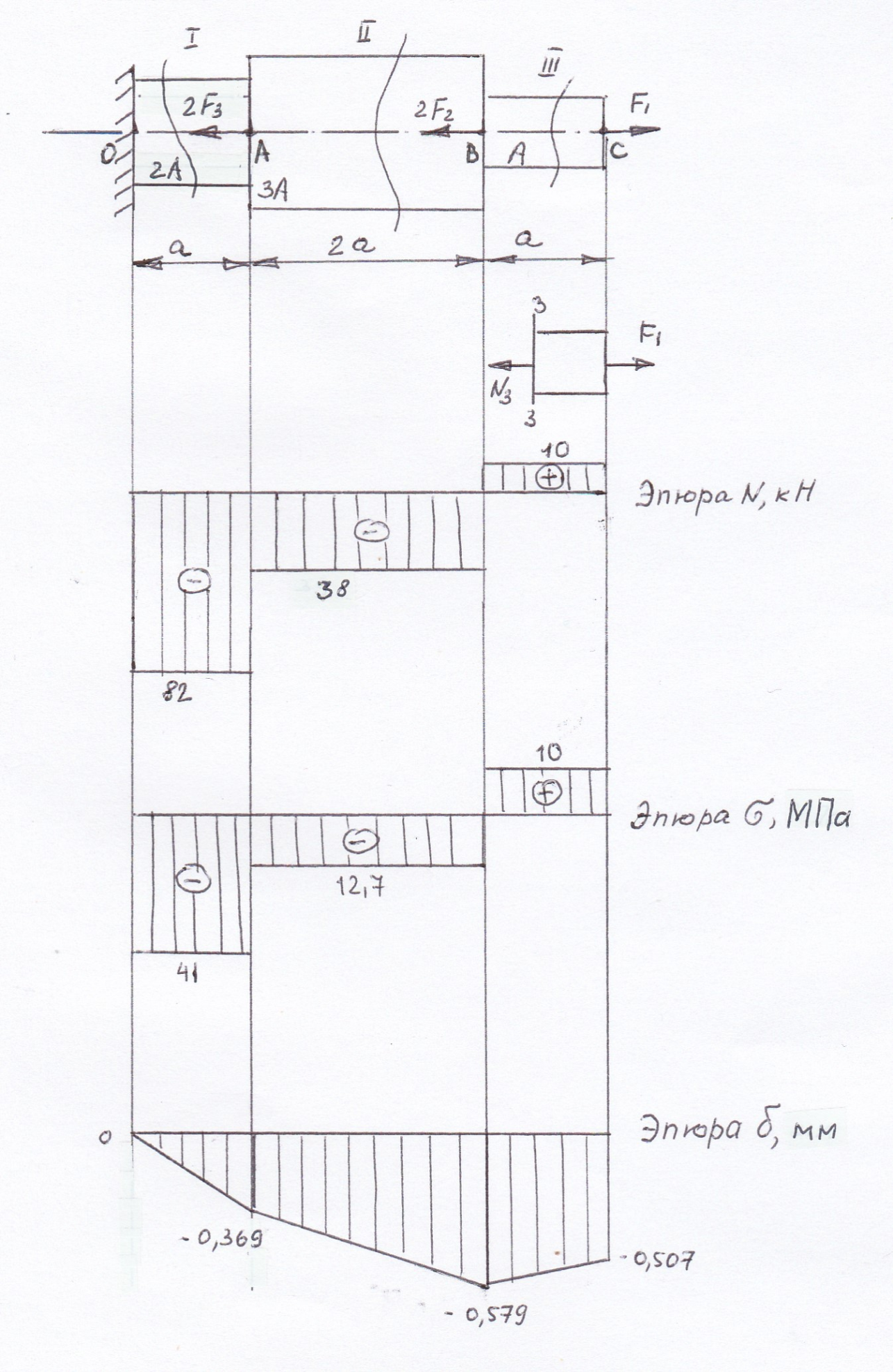
г.Нижневартовск, 2022 Задание 3 Центральное растяжение и сжатие прямых стержней переменного сечения Для стального ступенчатого стержня, 1 находящегося под действием сил Fi, приложенных в осевом направлении, требуется: 1) построить эпюры нормальных сил N, нормальных напряжений ; 2) построить эпюру осевых перемещений ; 3) определить его полное удлинение (укорочение) l. Исходные данные
Рисунок 3.1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| № п\п | Мощность, кВт | Длины участков, м | Угловая скорость , рад/с рад\с | =d/D | Допускаемые напряжения, , МПа | Допускаемый угол закручивания, , град\м | ||||||||
| P1 | P2 | P3 | a | b | c | |||||||||
| 3 | 90 | 40 | 60 | 0,5 | 0,3 | 0,6 | 28 | 0,9 | 30 | 0,45 | ||||
Решение
Определяем скручивающие моменты:
 ;
;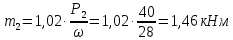 ;
;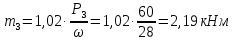 .
.2 Значение неизвестного момента m4 найдем из того условия, что угол закручивания свободного конца вала равен нулю, т.е. А=0. Для удобства счета разобьем этот угол на составляющие, зависящие от каждого скручивающего момента, т.е. φА = φтА+ φmА+ φт2+ φm3= 0 ,
где φтА - угол поворота концевого сечения от действия только момента тa,φm1- то же, но от действия только момента m1;
φm2 - от действия только момента т2; φт3 - от действия только момента m3;

Подставив числовые значения, после преобразований, получим:
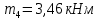
Пользуясь методом сечений, определяем величины крутящих моментов на отдельных участках вала.
Участок 1
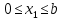

Участок 2
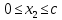
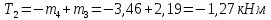
Участок 3
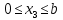
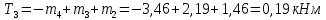
Участок 4


По полученным значениям крутящих моментов строим эпюру Т (рис. 4.2,б).
4. По условию прочности вала
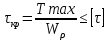
Найдем требуемое значение полярного момента сопротивления сечения

Для сплошного сечения вала:
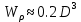 , тогда диаметр вала:
, тогда диаметр вала: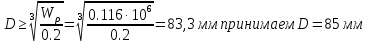
Для кольцевого сечения вала при α=d/D=0.9:
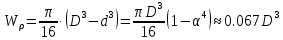 тогда диаметр вала:
тогда диаметр вала: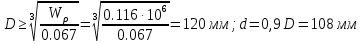
5. Вычислим углы поворота «» для круглого сечения вала:
Полярный момент инерции :

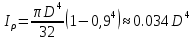
Жесткость сечения:
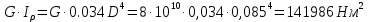
Углы закручивания участков:


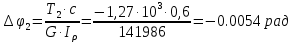
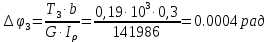
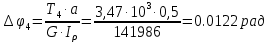
Углы поворота сечений:

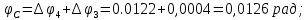

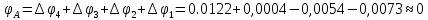
По полученным значениям строим эпюру углов поворота «» (рисунок 4.2в).
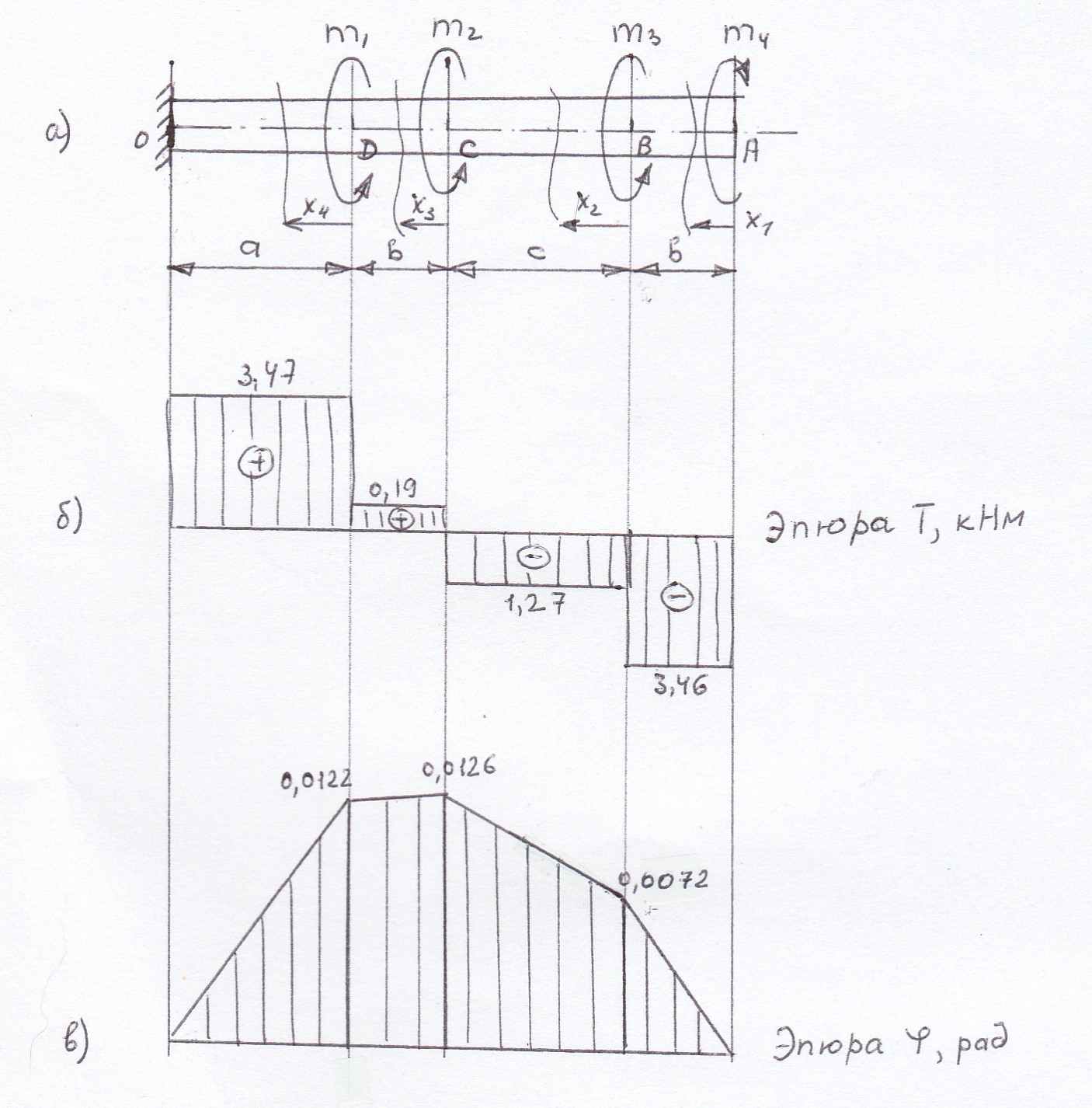
Рис.4.2
Задание 5
Плоский изгиб балочных систем.
Для заданной балки (рисунок 5.1) требуется:
1) построить эпюры поперечных сил Q, изгибающих моментов М;
2) подобрать;
- для балок с 1 по 6 схемы – из сортамента двутавровое сечение, материал балки – сталь []=160 МПа;
Исходные данные в таблице 5
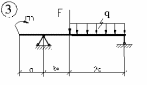
Рис.5.1
Таблица 5
| № п\п | Нагрузка | Длины участков, м | ||||
| F, кН | m, кНм | q, кН/м | a | b | c | |
| 3 | 40 | 40 | 30 | 3 | 3 | 2 |
Решение:
1 Определим опорные реакции
1. Определение опорных реакций.
Из условия статического равновесия балки на двух опорах найдем (рис. 5.2а):
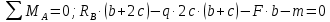

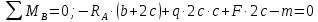

Проверка:
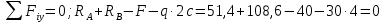

2. Изгибающие моменты и поперечные силы.
Выполним характерные сечения балки (I,II,III,) и запишем общие выражения для поперечной силы и изгибающего момента в сечениях.
Сечение I(
 )
)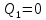

Сечение II (

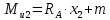 - уравнение I-ой степени
- уравнение I-ой степени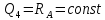
Численные значения


Сечение III (
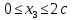 ) справа
) справа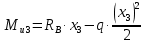 уравнение II-ой степени (данный участок эпюры принимает вид параболы)
уравнение II-ой степени (данный участок эпюры принимает вид параболы)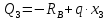 - уравнение I-ой степени
- уравнение I-ой степениЧисленные значения
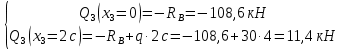
На участке знак поперечной силы изменяется в сечении с координатой:

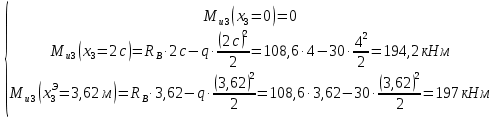
По расчетным данным строим эпюры Ми и Q (рис.5.2б,в)
Опасное сечение балки в точке , где на эпюре изгибающего момента наблюдается максимум

3. Подбор двутаврового сечения балки.
По условию прочности на изгиб по нормальным напряжениям найдем требуемый момент сопротивления опасного сечения:
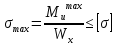
Где
 -изгибающий момент в опасном сечении, тогда
-изгибающий момент в опасном сечении, тогда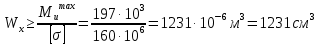
В сортаменте стальных прокатных профилей ГОСТ 8239-89 выбираем двутавр №45, у которого
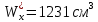
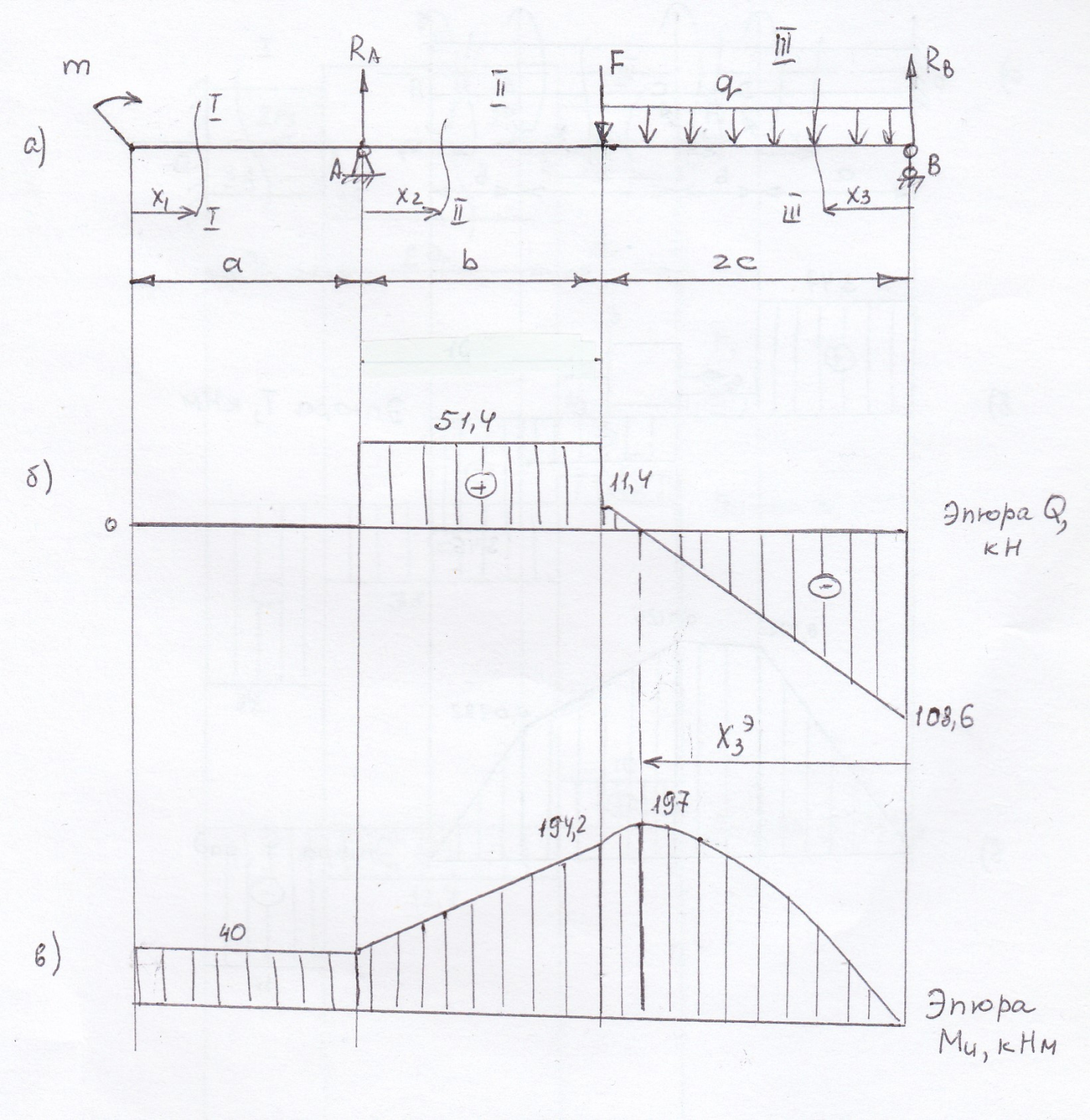
Рис.5.2

 , откуда
, откуда 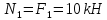
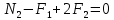 ,
,
 , откуда
, откуда