САиПР ЛР№1_v1. Факультет Информационных систем и технологий Кафедра Автоматизации предприятий связи

• Название: Факультет Информационных систем и технологий Кафедра Автоматизации предприятий связи
• Дата: 10.04.2022
• Размер: 86.91 Kb.
• Имя файла: САиПР ЛР№1_v1.docx
• Тип: Отчет; #458249

Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М.А. Бонч-Бруевича

Факультет «Институт непрерывного образования»

__________________________________________________________________

Факультет Информационных систем и технологий

Кафедра Автоматизации предприятий связи

Системный анализ и принятие решений

Отчет по лабораторной работе № 1

Принятие решений при планировании и управлении производством с учетом ресурсных ограничений

Фамилия:
Имя:
Отчество:
Курс:
Студ. билет № :
Группа №:
Проверил:

Санкт-Петербург

2020

Цель работы:

получение навыков применения методологии системного анализа при

моделировании и оптимизации функционирования производственной системы на примере расчета оптимальной производственной программы предприятия с учетом ограничений по ресурсам и спросу.
Задание:

Рассчитать оптимальный план выпуска продукции при условии, что прибыль от производства и реализации единицы каждого вида продукции принимает значение соответственно номеру варианта.

Ресурсы	Вид продукции					Уровень располагаемого ресурса
	Затраты ресурса на единицу продукции
	П1	П2	П3	П4
1.Трудовые	1	2	3	4	40
2.Материальные	6	5	4	3	110
3.Финансовые	4	6	8	12	100
Границы объема выпуска продукции:
нижняя	1	0	2	3
верхняя	12	-	-	3
Объем выпуска продукции	Х1	Х2	Х3	Х4
Прибыль от реализации единицы продукции	80	90	130	150
Себестоимость единицы продукции	200	220	300	330

Решение задачи:

На первом этапе требуется: определить такие объемы выпуска продукции каждого вида, которые бы обеспечили максимум прибыли при заданных ограничениях (по уровням наличных ресурсов и границам выпуска продукции);

Для решения оптимизационной задачи будем использовать программу “Lindo”.

Решение задачи на первом этапе.

Запись математической модели в соответствии с требованиями программы “Lindo”:

MAX 80X1 + 90X2 + 130X3 + 150X4

SUBJECT TO

R1) X1 + 2X2 + 3X3 + 4X4 <= 40

R2) 6X1 + 5X2 + 4X3 + 3X4 <= 110

R3) 4X1 + 6X2 + 8X3 + 12X4 <= 100

! Выражение для суммарной себестоимости

Sebst) 200 X1 + 220 X2 + 300 X3 +330 X4 >= 0

X1 >= 1

X1 <= 12

X2 >= 0

X3 >= 2

X4 = 3

END


Вид диалогового окна программы Lindo с записью математической модели и результатом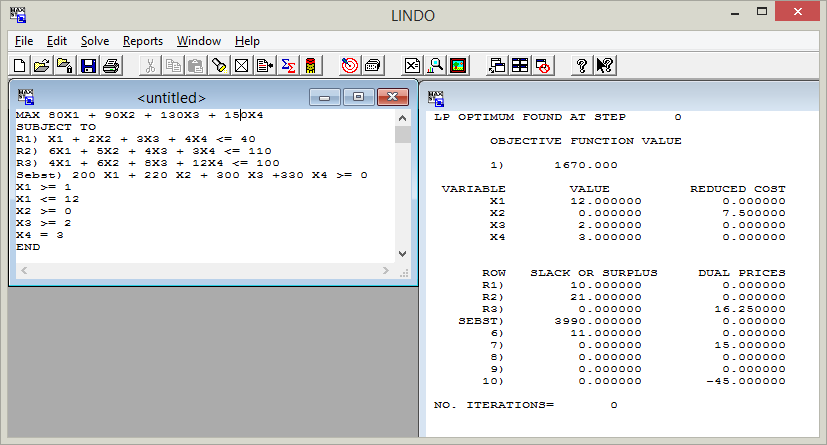


Оптимальное решение задачи:

1) Максимальное значение прибыли (Ропт) равно 1670 ед.

2) X1 = 12 – объем выпуска продукта П1;

X2 = 0 - объем выпуска продукта П2;

X3 = 2 - объем выпуска продукта П3;

X4 = 3 - объем выпуска продукта П4.

3) Суммарная себестоимость продукции S равна 3990 ед.

4) Количество неиспользуемого ресурса вида 1 (SLACK OR SUPPLUS) -10 ед. ресурса;

5) Количество неиспользуемого ресурса вида 2 (SLACK OR SUPPLUS) -21 ед. ресурса;

6) Количество неиспользуемого ресурса вида 3 (SLACK OR SUPPLUS) -0 ед. ресурса;

Коэффициент эффективности производственной системы: k = P/S = 1670/3990 = 0,419.
Решение задачи на втором этапе.
Запись математической модели в соответствии с требованиями программы “Lindo”:

MAX 0.025Y1 + 0.009Y2 + 0.01Y3

SUBJECT TO

R1) X1 + 2X2 + 3X3 + 4X4 + Y1 = 40

R2) 6X1 + 5X2 + 4X3 + 3X4 + Y2 = 110

R3) 4X1 + 6X2 + 8X3 + 12X4 +Y3 = 100

! Дополнительное условие – ограничение по прибыли

Prib) 80X1 + 90X2 + 130X3 +150X4 >= 1670

! Выражение для суммарной себестоимости

Sebst) 200 X1 + 220 X2 + 300 X3 +330 X4 >= 0

X1 >= 1

X1 <= 12

X2 >= 0

X3 >= 2

X4 = 3

END

Вид диалогового окна программы Lindo с записью математической модели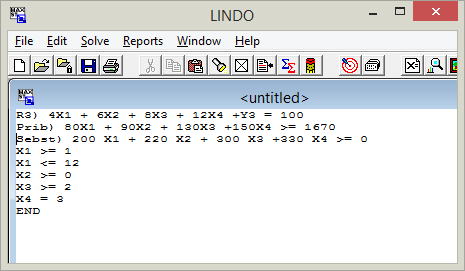



Результаты решения задачи на втором этапе: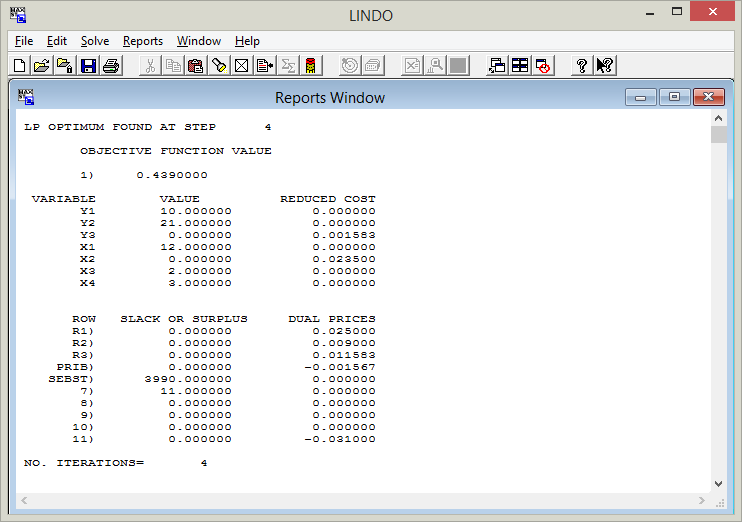


В оптимальном решении:

1) Значение целевой функции равно 0,439

2) Y1 = 10 – количество неиспользуемого ресурса вида 1;

Y2 = 21 - количество неиспользуемого ресурса вида 2;

Y3 = 0 - количество неиспользуемого ресурса вида 3;

3) X1 = 12 – объем выпуска продукта П1;

X2 = 0 - объем выпуска продукта П2;

X3 = 2 - объем выпуска продукта П3;

X4 = 3 - объем выпуска продукта П4.

4) Суммарная себестоимость S равна 3990 ед.

5) Прибыль (Р) равна 1670 ед.

Коэффициент эффективности производственной системы:

k = P/S = 1670/3440 = 0,419.

Вывод:

Таким образом, в результате проведения двухступенчатой оптимизации получен такой план выпуска продукции, который обеспечит получение максимально возможной при заданных ресурсах прибыли при максимально возможной экономии ресурсов.