Федеральное агентство по образованию Российской Федерации
Филиал «Севмашвтуз» государственного образовательного учреждения высшего профессионального образования «Санкт – Петербургский государственный морской технический университет»
в г. Северодвинске
ФАКУЛЬТЕТ: IV
КАФЕДРА ФИЗИКИ
ЛАБОРАТОРНАЯ РАБОТА
Определение момента инерции с помощью маятника Максвелла
СЕВЕРОДВИНСК
2007
ЛАБОРАТОРНАЯ РАБОТА ФМ - 12
Определение момента инерции с помощью маятника Максвелла
1. Цель и метод работы
1. Изучить теорию вращательного движения твёрдого тела вокруг неподвижной оси;
2. Путем измерения характеристик маятника Максвелла определить момент инерции маятника экспериментально и сравнить его с теоретическим значением.
2. Основные теоретические положения

  
Законы вращательного движения твердых тел сходны с законами поступательного движения, однако, при описании вращения твердого тела учитывается не просто его масса, а распределение этой массы относительно оси вращения (рис.1).
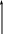   В В о вращательном движении твёрдого тела вокруг неподвижной оси все его точки движутся по окружностям некоторых радиусов, причем, за время Dt радиусы любых точек тела поворачиваются на одинаковый угол поворота Dj. Угол поворота о вращательном движении твёрдого тела вокруг неподвижной оси все его точки движутся по окружностям некоторых радиусов, причем, за время Dt радиусы любых точек тела поворачиваются на одинаковый угол поворота Dj. Угол поворота  радиуса R является аксиальным вектором (или псевдовектором) и откладывается вдоль оси вращения, согласно правилу правого винта. Скорость вращения можно оценивать угловой скоростью радиуса R является аксиальным вектором (или псевдовектором) и откладывается вдоль оси вращения, согласно правилу правого винта. Скорость вращения можно оценивать угловой скоростью  определяемая выражением определяемая выражением

Δt → 0
 . .
Вектор  по направлению совпадает с вектором по направлению совпадает с вектором  , а его модуль углу поворота тела в единицу времени , а его модуль углу поворота тела в единицу времени  ; для равномерного вращения ; для равномерного вращения  ; n - частота вращения; Т – период вращения или время одного оборота. ; n - частота вращения; Т – период вращения или время одного оборота.
Скорость изменения вектора  определяется вектором углового ускорения определяется вектором углового ускорения  : :

Δt → 0
 . .
Если направление оси вращения в пространстве не изменяется, вектор  может изменяться только по модулю. В этом случае векторы может изменяться только по модулю. В этом случае векторы  и и  коллинеарны, причем направлены в одну сторону, если вращение ускоренное (рис. 2 а), и в противоположные стороны, если вращение замедленное (рис. 2 б). коллинеарны, причем направлены в одну сторону, если вращение ускоренное (рис. 2 а), и в противоположные стороны, если вращение замедленное (рис. 2 б).
а) б)
Рис. 2
 У У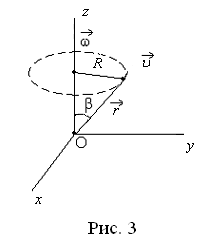 гловая скорость гловая скорость  и ускорение и ускорение  для всех точек вращающегося тела в данный момент времени одинаковы, однако, для различных точек тела линейные скорости для всех точек вращающегося тела в данный момент времени одинаковы, однако, для различных точек тела линейные скорости  движения по окружности разные, так как зависят от расстояния R точки до оси вращения. Модуль линейной скорости точки определяется выражением движения по окружности разные, так как зависят от расстояния R точки до оси вращения. Модуль линейной скорости точки определяется выражением
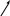  . .
 Итак, Итак,  . Для неравномерного вращения нормальное ускорение . Для неравномерного вращения нормальное ускорение  и тангенциальное ускорение и тангенциальное ускорение
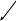  . .
В общем случае векторы    связаны векторными произведениями: связаны векторными произведениями:  и и  (рис. 3). (рис. 3).
При отсутствии внешних воздействий или результирующем моменте внешних сил, равном нулю, всякое тело, имеющее ось вращения, будет сохранять состояние покоя или равномерного вращения.
Рассмотрим вращение твердого тела массой m, вокруг некоторой оси ОО1 под действием внешних сил. Разобьем это тело на элементарные объемы с массой mi (рис. 4).
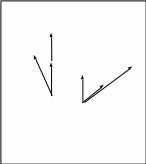
Пусть  - равнодействующая внешних и внутренних сил, приложенных к i – ому элементарному объему тела. Разложим - равнодействующая внешних и внутренних сил, приложенных к i – ому элементарному объему тела. Разложим  на составляющие Fi׀׀, Fit и Fi^, где Fi^ - перпендикулярно оси ОО1, сила Fi׀׀ – параллельно оси вращения и Fit - по касательной к окружности (траектории движения i – ого элементарному объема. на составляющие Fi׀׀, Fit и Fi^, где Fi^ - перпендикулярно оси ОО1, сила Fi׀׀ – параллельно оси вращения и Fit - по касательной к окружности (траектории движения i – ого элементарному объема.
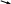 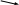 При движении точки mi силы Fi׀׀ и Fit ускорение этой массе не сообщают, а сила При движении точки mi силы Fi׀׀ и Fit ускорение этой массе не сообщают, а сила  сообщает касательное ускорение, аt. сообщает касательное ускорение, аt. По второму закону Ньютона  . . Момент  силы силы  равен равен  . . Умножим правую и левую части формулы  на радиус окружности ri: на радиус окружности ri:
 , ,
где  - угловое ускорение. - угловое ускорение.
Величина  - называется моментом инерции материальной точки, относительно оси (произведение массы материальной точки на квадрат расстояния до оси вращения). - называется моментом инерции материальной точки, относительно оси (произведение массы материальной точки на квадрат расстояния до оси вращения).
 , здесь Mi - момент силы, действующей на материальную точку. , здесь Mi - момент силы, действующей на материальную точку.
Причем  , т.к. , т.к.  . .
Величина  - момент инерции всего тела, равный сумме моментов инерции всех точек, составляющих это тело. - момент инерции всего тела, равный сумме моментов инерции всех точек, составляющих это тело.
Итак,  или или  получили выражение второго закона механики для вращательного движения: вектор момента внешних сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение, полученное телом. получили выражение второго закона механики для вращательного движения: вектор момента внешних сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение, полученное телом.
Таким образом, во вращательном движении роль силы выполняет момент силы, роль массы - момент инерции, а роль ускорения – угловое ускорение.
Момент инерции  является мерой инертности тела во вращательном движении, характеризует его инертные свойства и показывает, что они зависят не только от величины, но и от характера распределения массы тела относительно оси вращения. является мерой инертности тела во вращательном движении, характеризует его инертные свойства и показывает, что они зависят не только от величины, но и от характера распределения массы тела относительно оси вращения.
Если известен момент инерции тела относительно оси ОО1, проходящей через его центр масс С, то момент инерции тела относительно произвольной оси КК1, параллельной данной ОО1, можно вычислить по теореме Штейнера:  , ,
где d – расстояние между осями (рис.5), m – масса тела.
Величина  - называют моментом импульса (или моментом количества движения) материальной точки, а величина - называют моментом импульса (или моментом количества движения) материальной точки, а величина  называется моментом импульса тела. Поскольку, называется моментом импульса тела. Поскольку,
   
d
d

О
К
и  , то момент внешних сил: , то момент внешних сил:
 , ,
откуда  или или  , где , где  - приращение момента импульса за время - приращение момента импульса за время 
Выражение  есть другая форма записи для второго закона Ньютона. Если момент внешних сил, действующих на тело, равен нулю, т.е. есть другая форма записи для второго закона Ньютона. Если момент внешних сил, действующих на тело, равен нулю, т.е.  , то , то  , т.е. момент импульса изолированного тела есть величина постоянная. Мы получили закон сохранения момента импульса. , т.е. момент импульса изолированного тела есть величина постоянная. Мы получили закон сохранения момента импульса.
3. Описание опытной установки
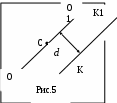
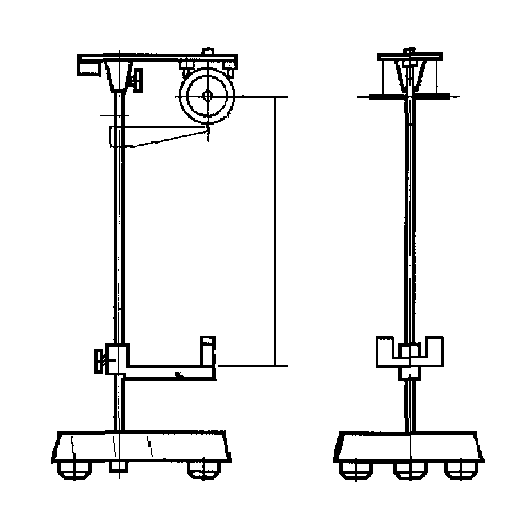
Изучение закона сохранения энергии, основано на измерениях, полученных из характеристик мятника Максвелла. Установка представлена на рис. 6 и включает в состав: основание 1, вертикальную стойку 2, верхний кронштейн 3, кронштейн 4 для установки фотодатчика, фотодатчик 5, диск 6 с осью, подвешенной на двух нитях 7, комплект из трех сменных колец с различными моментами инерции.
Основание снабжено тремя регулируемыми опорами 8 и зажимом 9 для фиксации вертикальной стойки 2.
Вертикальная стойка 2 выполнена из металлической трубы, на которую нанесена миллиметровая шкала, и имеет визир 12.
На верхнем кронштейне 3 размещаются электромагниты 10 и узел 11 регулировки исходного положения маятника.
Кронштейн 4 имеет зажим для крепления на вертикальной стойке 2 и элементы фиксации фотодатчика.
Установка работает от блока электронного ФМ 1/1.
Общий вид установки вместе с электронным блоком представлен в приложении 1.
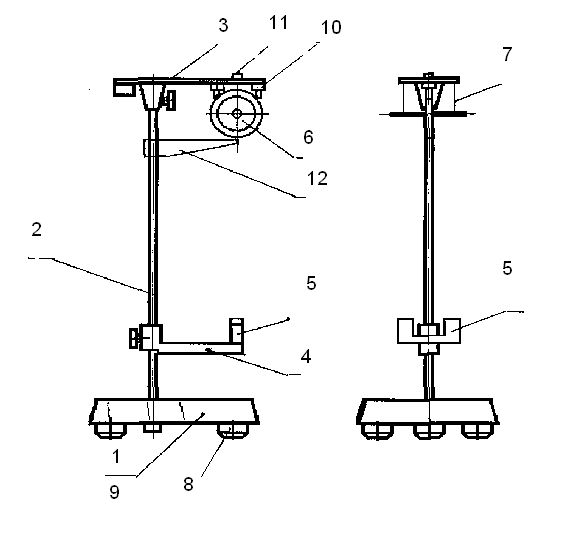
Рис.6
4. Вывод рабочей формулы
2r
D
h
В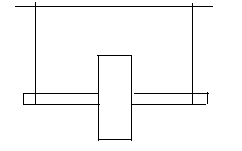 данной работе определяют момент инерции с помощью маятника Максвелла. Для вывода расчетной формулы применим закон сохранения энергии, считая движущийся диск с осью консервативной системой. Наматывая на ось диска нить подвеса, поднимем его на высоту h. При этом диск приобретет потенциальную энергию Е=mgh, где m – масса диска. При раскручивании нити опускающийся диск движется поступательно и одновременно вращается вокруг своей оси. При этом потенциальная энергия диска превращается в кинетическую. По закону сохранения энергии для момента времени, когда диск опустится с высоты h, имеем (рис. 7) данной работе определяют момент инерции с помощью маятника Максвелла. Для вывода расчетной формулы применим закон сохранения энергии, считая движущийся диск с осью консервативной системой. Наматывая на ось диска нить подвеса, поднимем его на высоту h. При этом диск приобретет потенциальную энергию Е=mgh, где m – масса диска. При раскручивании нити опускающийся диск движется поступательно и одновременно вращается вокруг своей оси. При этом потенциальная энергия диска превращается в кинетическую. По закону сохранения энергии для момента времени, когда диск опустится с высоты h, имеем (рис. 7)

Рис. 7
 , (1) , (1)
где  - скорость поступательного движения диска; J - момент инерции диска с осью относительно оси, проходящей через геометрический центр диска; w - угловая скорость вращения диска; - скорость поступательного движения диска; J - момент инерции диска с осью относительно оси, проходящей через геометрический центр диска; w - угловая скорость вращения диска;  - кинетическая энергия диска в поступательном движении; - кинетическая энергия диска в поступательном движении;  - кинетическая энергия диска во вращательном движении. - кинетическая энергия диска во вращательном движении.
Так как равноускоренное движение диска начинается из состояния покоя, то
 , ,  (2) (2)
здесь t - время опускания диска с высоты h.
Из формул (2) получаем
 . (3) . (3)
Угловая скорость вращающегося диска определяется формулой
 , (4) , (4)
в которой r - диаметр оси диски.
Подставляя (3) в (4), получим
 . (5) . (5)
Заменив в соотношении (1)  и w выражениями (3) и (5), получим формулу для момента инерции диска: и w выражениями (3) и (5), получим формулу для момента инерции диска:
 . (6) . (6)
Для нашей установки gt2/2h>>1, с учетом этого неравенства выражение (6) примет вид
 (7) (7)
Уравнение (7) является рабочей формулой данной лабораторной работы.
Таким образом, для определения момента инерции с помощью маятника Максвелла маятника Максвелла нужно измерить величины m, r, h, t.
5. Порядок проведения работы
1. Установить кронштейн с фотодатчиком в крайнее нижнее положение шкалы так, чтобы плоскость кронштейна, окрашенная в синий цвет, совпала с одной из рисок шкалы.
2. Произвести регулировку положения основания при помощи регулировочных опор так, чтобы диск на бифилярном подвесе находился в центре окна фотодатчика.
3. Установить с помощью узла регулировки 11 (рис. 7) необходимую длину бифилярного подвеса таким образом, чтобы нижний край среза сменного кольца маятника находился на 4-5 мм ниже оптической оси фотодатчика; при этом ось маятника должна занимать горизонтальное положение.
4. Подключить фотодатчик и электромагниты установки к блоку электронному при помощи кабеля. Вилку с маркировкой “Ф” вставить в розетку фотодатчика, а вилку с маркировкой “Э” в розетку электромагнитов.
5. Нажать кнопку “СЕТЬ”. При этом должно включиться табло индикации и должны включиться электромагниты.
6. Вращая маятник по часовой стрелке, зафиксировать его в верхнем положении при помощи левого (ближнего к стойке) электромагнита, при этом необходимо следить за тем, чтобы нить наматывалась на ось виток к витку. При вращении маятника против часовой стрелки фиксировать маятник необходимо при помощи правого (дальнего от стойки) электромагнита.
7. Нажать кнопку “СБРОС” для того, чтобы убедиться, что на табло устанавливаются нули.
8. При нажатии кнопки “ПУСК” на блоке электромагниты должны обесточиться, маятник должен начать раскручиваться, таймер должен произвести отсчет времени, а в момент пересечения маятником оптической оси фотодатчика отсчет времени должен прекратиться.
9. При помощи визира по шкале вертикальной стойки определить высоту, с которой опускается маятника, h.
10. Нажать кнопку “СБРОС”. Привести маятник в исходное положение (зафиксировать в верхнем положении при помощи электромагнита).
11. Нажать кнопку “ПУСК” на блоке.
12. Записать показание таймера, т.е. время хода маятника t.
13. Полученные результаты измерений записать в табл. 1
Таблица 1
№
|
t,
c
|
m,
кг
|
D,
м
|
h,
м
|
Ji,
кг·м2
|
Jср,
кг·м2
|
DJi,
кг·м2
|
DJср,
кг·м2
|
dJ,
кг·м2
|
 Jэксп, Jэксп,
кг·м2
|
Jтеор,
кг·м2
|
1
|
1,410
|
0,12335
|
0,09
|
0,27
|
0,00007121
|
|
0,00028841
|
|
|
|
|
2
|
1,401
|
0,13769
|
0,09
|
0,268
|
0,00007906
|
|
0,00028056
|
|
|
|
|
3
|
2,072
|
0,30697
|
0,09
|
0,264
|
0,00039137
|
0,00035962
|
0,00003175
|
0,00022758
|
6,32834659
|
0,00035962
+-
0,00022758
|
0,000124891
|
4
|
2,136
|
0,39929
|
0,09
|
0,264
|
0,00054101
|
|
0,00018139
|
|
|
|
|
5
|
2,225
|
0,48663
|
0,09
|
0,264
|
0,000715485
|
|
0,000355815
|
|
|
|
|
6. Обработка результатов опыта
1. Рассчитать момент инерции для каждого измерения по формуле
 . .
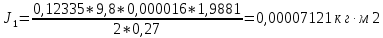
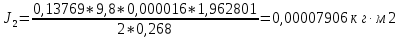
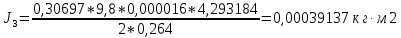
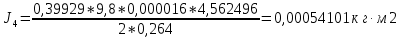
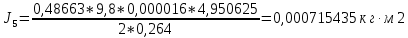
2. Найти среднее значение момента инерции:

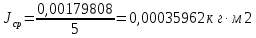
3. Определить абсолютную погрешность для каждого значения момента инерции, т.е.
 , ,  , ,  , ,  , , 
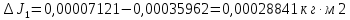
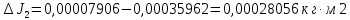
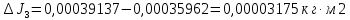
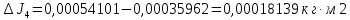
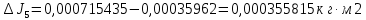
4. Рассчитать среднюю абсолютную погрешность момента инерции

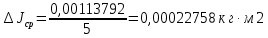
5. Найти относительную погрешность измерений момента инерции

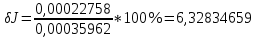 кг·м2 кг·м2
6. Записать искомый результат

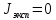 ,00035962+-0,00022758 ,00035962+-0,00022758
7. Рассчитать теоретическое значение момента инерции

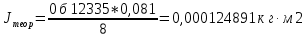
и сравнить его с экспериментальным значением.
8. Полученные данные занести в табл. 1.
Приложение 1

Указание мер безопасности
1. К работе с установкой допускаются лица, ознакомленные с ее устройством, принципом действия и мерами безопасности в соответствии с требованиями, приведенными в настоящем разделе.
2. Для обеспечения нормальной работы установки и предотвращения выхода из строя фотодатчика подключение установки к блоку электронному производить строго в соответствии с описанием.
3. Для предотвращения опрокидывания установки необходимо располагать ее только на горизонтальной поверхности.
Контрольные вопросы
Что называется моментом инерции материальной точки, твёрдого тела?
Момент инерции - величина, характеризующая меру инерции материальной точки при её вращательном движении вокруг оси. Численно она равна произведению массы на квадрат радиуса (расстояния до оси вращения). Для твердого тела момент инерции равен сумме моментов инерции её частей, и поэтому может быть выражена в интегральной форме:
I=∫ r2 dү.
Сформулируйте второй закон механики для вращательного движения.
Продифференцировав момент импульса по времени, получим основное уравнение динамики вращательного движения, известное как второй закон Ньютона для вращательного движения, формулируемый следующим образом: скорость изменения момента импульса L тела, вращающегося вокруг неподвижной точки, равна результирующему моменту всех внешних сил M, приложенных к телу, относительно этой точки:
dL/dt = M (1)
Так как момент импульса вращающегося тела прямо пропорционален угловой скорости вращения, а производная d/dt есть угловое ускорение , то это уравнение может быть представлено в виде
J = M (2)
где J – момент инерции тела.
Уравнения (1) и (2), описывающие вращательное движение тела, по своему содержанию аналогичны второму закону Ньютона для поступательного движения тел (ma = F). Как видно, при вращательном движении в качестве силы F используется момент силы M, в качестве ускорения a – угловое ускорение , а роль массы m, характеризующей инерционные свойства тела, играет момент инерции J.
Что называется моментом импульса?
Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется. 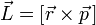
Сформулируйте закон сохранения момента импульса.
Закон сохранения момента импульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Выведите рабочую формулу.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде:  , если система находится в равновесии. , если система находится в равновесии.
6. Как определить погрешность измерений?
Лабораторная работа утверждена на заседании кафедры от
31 августа 2007 г. протокол №1.
Заведующий кафедрой №12
Д.т.н. профессор Горин С.В. |
 Скачать 498.34 Kb.
Скачать 498.34 Kb.
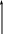

 В
В о вращательном движении твёрдого тела вокруг неподвижной оси все его точки движутся по окружностям некоторых радиусов, причем, за время Dt радиусы любых точек тела поворачиваются на одинаковый угол поворота Dj. Угол поворота
о вращательном движении твёрдого тела вокруг неподвижной оси все его точки движутся по окружностям некоторых радиусов, причем, за время Dt радиусы любых точек тела поворачиваются на одинаковый угол поворота Dj. Угол поворота 
 .
.
 .
.




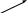

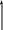 У
У гловая скорость
гловая скорость 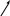
 Итак,
Итак, 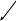

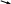
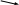 При движении точки mi силы Fi׀׀ и Fit ускорение этой массе не сообщают, а сила
При движении точки mi силы Fi׀׀ и Fit ускорение этой массе не сообщают, а сила  Jэксп,
Jэксп,
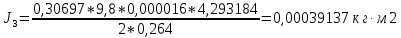
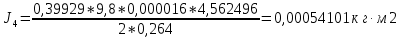
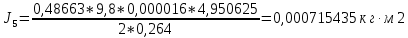
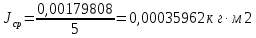
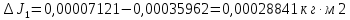
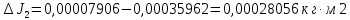
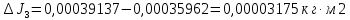
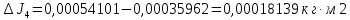
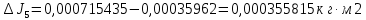
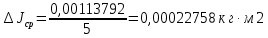
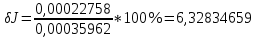 кг·м2
кг·м2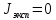 ,00035962+-0,00022758
,00035962+-0,00022758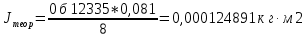



















 данной работе определяют момент инерции с помощью маятника Максвелла. Для вывода расчетной формулы применим закон сохранения энергии, считая движущийся диск с осью консервативной системой. Наматывая на ось диска нить подвеса, поднимем его на высоту h. При этом диск приобретет потенциальную энергию Е=mgh, где m – масса диска. При раскручивании нити опускающийся диск движется поступательно и одновременно вращается вокруг своей оси. При этом потенциальная энергия диска превращается в кинетическую. По закону сохранения энергии для момента времени, когда диск опустится с высоты h, имеем (рис. 7)
данной работе определяют момент инерции с помощью маятника Максвелла. Для вывода расчетной формулы применим закон сохранения энергии, считая движущийся диск с осью консервативной системой. Наматывая на ось диска нить подвеса, поднимем его на высоту h. При этом диск приобретет потенциальную энергию Е=mgh, где m – масса диска. При раскручивании нити опускающийся диск движется поступательно и одновременно вращается вокруг своей оси. При этом потенциальная энергия диска превращается в кинетическую. По закону сохранения энергии для момента времени, когда диск опустится с высоты h, имеем (рис. 7)