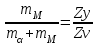ргр 7 вариант. Фазовые равновесия в двухкомпонентных металлических системах
 Скачать 5.01 Mb. Скачать 5.01 Mb.
|
|
Министерство науки и высшего образования Российской Федерации ФГБОУ ВО «Магнитогорский государственный технический университет имени Г.И. Носова» Кафедра металлургии и химической технологии РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №2 По дисциплине «Физическая химия» Раздел «Фазовые равновесия в двухкомпонентных металлических системах» Выполнил(а) Студент гр. __-__ _________ Проверила Профессор, к.т.н. . Магнитогорск 2022 ВВЕДЕНИЕИнженеру, специализирующемуся в области металловедения и термической обработки металлов, необходимо ориентироваться в громадном количестве сплавов, используемых в настоящее время в технике. Он должен знать, как связаны свойства сплавов с их структурой и как методами термической обработки обеспечить необходимую структуру, а значит и свойства металлических изделий. Первый этап на пути приобретения этих знаний – знакомство с диаграммами состояния металлических систем и методом их анализа. Диаграммы состояния смешанных систем строят в координатах температура - состав. В ряде случаев, а именно: для металлов, ограниченно растворимых друг в друге, обладающих полиморфизмом и дающих несколько химических соединений, диаграммы состояния сложны. Однако все они (и простые, и сложные) содержат одни и те же геометрические элементы, чередующиеся в определенной последовательности. Это облегчает анализ любой диаграммы состояния. Настоящие методические указания помогут студентам научиться «читать» диаграммы состояния систем из двух компонентов и познакомят их с расчетом ветвей ликвидуса в простейшей системе с эвтектическим превращением. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ1. ДИАГРАММЫ СОСТОЯНИЯ И ФИЗИКО-ХИМИЧЕСКИЙ АНАЛИЗФазовое равновесие в многокомпонентных системах изучают при помощи физико-химического анализа. В основе этого метода лежит исследование зависимостей различных физических свойств смешанных систем от состава. Частным случаем диаграмм состав - свойство являются диаграммы состояния или фазовые диаграммы. Они выражают зависимость температур равновесных фазовых переходов от состава системы. По диаграммам состояния можно судить о числе и природе фаз образующихся в системе, и условиях их существования, о температурах начала и конца различных фазовых переходов, совершающихся при изменении температуры, о составах равновесных фаз и количественном соотношении между ними при различных температурах, а также о возможности пластической деформации и термической обработки металлических сплавов. 2. ПРИРОДА КОНДЕНСИРОВАННЫХ ФАЗ И ВОЗМОЖНОЕ ИХ ЧИСЛОВ двухкомпонентных металлических системах конденсированные фазы могут быть жидкими и твердыми. Жидкие фазы – это расплавы или ненасыщенные растворы одного вещества в другом, т. е. фазы переменного состава. Им на диаграммах состояния удовлетворяют поля. В различных системах общее число жидких фаз может быть разным (рис. 1). 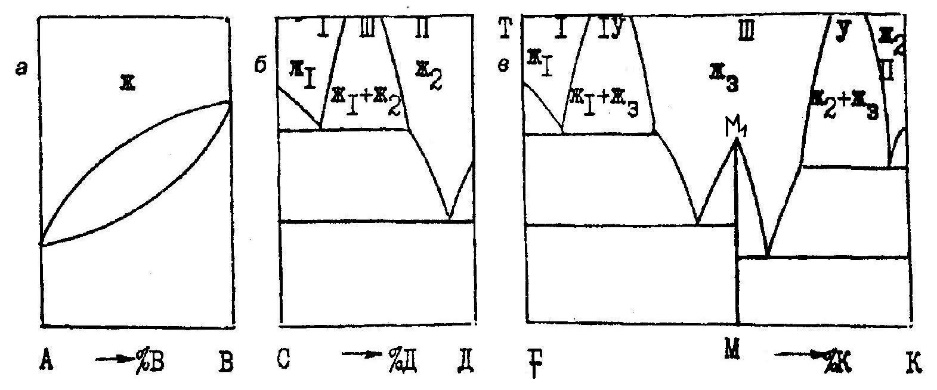 Рис. 1. Диаграммы состояния систем с различным числом жидких фаз В системе А-В (рис.1, а) компоненты неограниченно растворимы друг в друге и дают одну жидкую фазу – ненасыщенный раствор из вещества А и В, устойчивый в верхнем поле диаграммы. В системе С-Д (рис. 1, б) с ограниченной растворимостью компонентов две жидкие фазы (Ж1 и Ж2). Поля их устойчивости I и II примыкают к граничным вертикалям и разделяются областью расслоения III, где в равновесии присутствуют две несмешивающиеся жидкости. Каждый из растворов Ж1 и Ж2 обогащен одним из компонентов, он и выступает в роли растворителя. В расплаве Ж1 растворитель – вещество С, а в расплаве Ж2 – вещество Д. В системе F-К (рис. 1, в) с химическим соединением М жидких фаз три (Ж1, Ж2, Ж3), поля их существования I, II и III разделены двумя областями расслоения IV и V. В расплаве Ж3 преобладает химическое соединение М, оно и является растворителем. Твердые фазы. Они могут быть трех типов: 1. Чистые компоненты, образующие систему. Им на диаграмме состояния отвечают граничные ординаты. Если в твердом состоянии компонент имеет одну кристаллическую модификацию, то на граничной вертикали есть лишь одна критическая точка – его температура кристаллизации (плавления). Например, для вещества В (рис. 2) точка В1 соответствует его температуре плавления (кристаллизации). При температурах выше точки В1 компонент В устойчив в жидкой фазе, а при температурах ниже точки В1 – в твердой фазе. 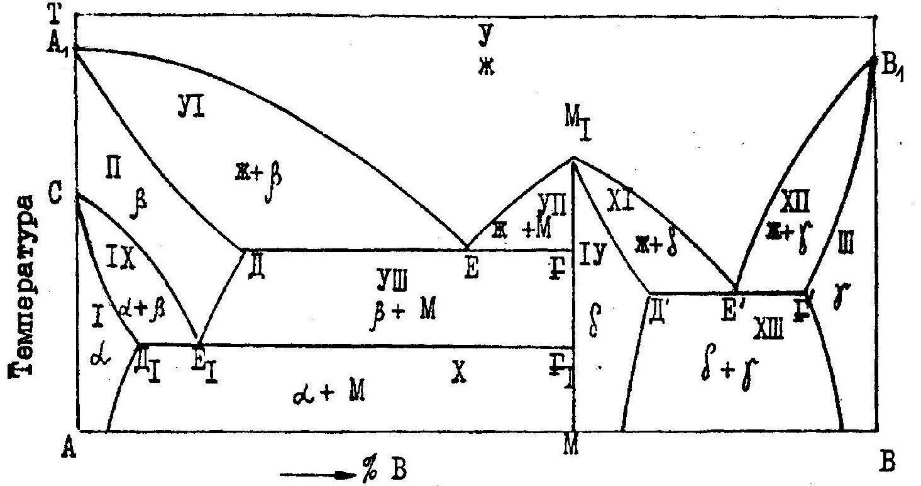 Рис. 2. Диаграмма состояния системы с несколькими твердыми фазами переменного состава Если же компонент системы обладает полиморфизмом, то на соответствующей ему граничной вертикали отмечается несколько критических точек – температур фазовых переходов. В этом случае компонент дает несколько твердых фаз (их число совпадает с числом кристаллических модификаций). Например, для вещества А (см. рис. 2) две критические точки: точка «С» отвечает температуре фразового перехода Аα=Аβ из одной кристаллической модификации (α) в другую (β) и точка А1 соответствует температуре плавления вещества А. При температурах ниже Тс – компонент устойчив в α модификации, в интервале температур от Тс до 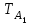 – в β модификации, а при Т > – в β модификации, а при Т > 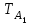 – в жидкой фазе. – в жидкой фазе.2. Химические соединения или фазы постоянного состава. Их в системе может быть несколько. На диаграмме состояния им удовлетворяют вертикальные линии. Например, линии ММ1 на рис. 1, в и 2. 3. Твердые растворы (фазы переменного состава). Твердым растворам, как и жидким, на диаграмме состояния удовлетворяют поля, они примыкают к граничным ординатам или вертикалям, отвечающим химическим соединениям. Например, в системе А—В (см. рис. 1, а) компоненты неограниченно растворимы в твердой фазе, поэтому образуется ненасыщенный твердый раствор, поле существования которого располагается в нижней части диаграммы. В системе, изображенной на рис. 2, таких твердых фаз четыре α, β, γ, δ. Поля I, II, III, где устойчивы твердые растворы α, β, γ, δ, соответственно примыкают к граничным ординатам, а поле устойчивости δ – раствора (IV) – к вертикали химического соединения М. В случае ограниченной растворимости фаз в твердом растворе сохраняется кристаллическая структура растворителя. Из диаграммы состояния (см. рис. 2) можно заключить, какой компонент в каждом из твердых растворов выполняет роль растворителя, а какой – роль растворенного вещества:
3. ПРИМЕНЕНИЕ ПРАВИЛА ФАЗ И ПРИНЦИП СООТВЕТСТВИЯСогласно принципу соответствия, вытекающему из правила фаз, каждой совокупности равновесно сосуществующих фаз на диаграмме состояния отвечает свой геометрический образ. Поэтому все диаграммы состояния любой сложности содержат одни и те же геометрические элементы. Правило фаз Гиббса С = к + n – ф для металлических систем из двух компонентов (к=2) при n=1 (из внешних параметров, влияющих на положение равновесия, учитывается только температура) приобретает вид С = 3 – Ф, где С – число термодинамических степеней свободы (вариантность системы); Ф – число конденсированных фаз, находящихся в равновесии. Рассмотрим возможные случаи. 1. Системе одна фаза – ненасыщенный раствор (жидкий или твердый). Тогда Ф=1 и С=2. Система имеет две степени свободы. Это означает, что независимо друг от друга можно изменять, в известных пределах, значения двух параметров (температуру и состав), и при этом будет существовать одна фаза. Такому условию на диаграмме состояния удовлетворяет поле гомогенности. Поля существования жидких фаз (расплавов) располагаются в верхней части диаграммы и снизу ограничиваются наклонными линиями – линиями насыщения (поля I и II на рис. 1, б; I—III на рис. 1, в; поле V на рис. 2). Поля устойчивости твердых ненасыщенных растворов примыкают к вертикалям, отвечающим чистым компонентам или химическим соединениям при температурах ниже температур конца кристаллизации. Эти поля сверху (а некоторые снизу) ограничиваются наклонными линиями (поля I—IV на рис. 2). 2. Равновесие двух фаз (две несмешивающиеся жидкости; два твердых раствора или твердый раствор и жидкая фаза). В этом случае Ф=2 и С=1. Система одновариантная. Это значит, что параметры – температура и состав каждой из равновесно сосуществующих фаз – взаимосвязаны одним уравнением. На диаграмме состояния этими уравнениями описываются наклонные линии или линии насыщения одних фаз другими. До этих линий и простираются поля гомогенности. Между линиями насыщения располагается поле гетерогенности – поле устойчивости двух равновесных фаз, в пределах которого число степеней свободы С=1. Из правила фаз следует, что в смежных полях диаграммы число фаз, а значит и степеней свободы, отличается на единицу. Это следствие облегчает анализ фазовых диаграмм, особенно сложных. После того, как определены поля гомогенности в любой системе, нетрудно установить, какие фазы существуют в равновесии в любом поле гетерогенности. Ими будут фазы, чьи поля или линии постоянного состава (вертикали) располагаются по обе стороны от рассматриваемого поля гетерогенности. В качестве примера в системе (см. рис. 2) расписаны все поля гомогенности (I—V) и гетерогенности (VI—XIII). 3. Равновесие трех фаз (двух жидких и одной твердой; двух твердых и одной жидкой, либо трех твердых). При этом Ф=3 и С=0. Система безвариантна, т. е. совместное равновесие трех фаз возможно лишь при постоянной температуре и неизменных составах фаз (ни один из параметров произвольно меняться не может). На диаграмме состояния этому удовлетворяет участок горизонтальной линии с тремя точками, указывающими составы равновесных фаз (горизонтальные линии на рис. 1, б, в и на рис. 2). Например, при температуре точки «Е» (см. рис. 2) горизонталь ДЕF отвечает равновесию трех фаз, составы которых указывают точки «Д», «Е» и «F». В 1-й фазе %В=«Д» – это насыщенный β – твердый раствор, так как точка «Д» принадлежит полю II. Во 2-й фазе %В=«F» – это кристаллы химического соединения, так как точка «F» находится на вертикали ММ1 при температуре ТF ниже температуры кристаллизации. В третьей фазе %В=«E» – это расплав (жидкая фаза). Из правила фаз вытекает, что в двухкомпонентной системе одновременно в равновесии не может находиться более трех фаз (число степеней свободы не может быть отрицательным). Таким образом, двухкомпонентные диаграммы состояния любой сложности – это совокупность полей гомогенности и гетерогенности, разделенных различными линиями: — наклонными (линии насыщения одних фаз другими); — вертикальными (линии постоянного состава, отвечающие химическим соединениям); — горизонтальными (линии равновесного сосуществования трех конденсированных фаз). Переходя от одного поля к другому, при движении слева на-право, наблюдаем смену полей гомогенности и гетерогенности (см. рис. 2, поля II, VI, V, VII, IV, XI, V, XII, III). При движении сверху вниз в отсутствии горизонтальных линий на диаграмме поля гомогенности и гетерогенности также чередуются (см. рис. 2, поля V, VI, II, IX, I). Если же при таком движении встречаются горизонтальные линии, то выше и ниже них размещаются поля гетерогенности (см. рис. 2, линия ДЕF и поля VI, VII, VIII; линия Д'Е'F' и поля XI, XII, XIII; линия Д1E1F1 и поля VIII, IX, X). 4. ЛИНИИ ЛИКВИДУСА И СОЛИДУСА И ПРИНЦИП НЕПРЕРЫВНОСТИЛюбое чистое вещество кристаллизуется или плавится при постоянной температуре, так как при равновесии двух фаз (жидкой и твердой) число степеней свободы С=0. Равновесие одной твердой фазы и двухкомпонентного расплава возможно в интервале температур (С=1). Для таких систем различают температуры начала и конца кристаллизации или начала и конца плавления. Линия, выражающая зависимость температур начала равновесной кристаллизации одной твердой фазы из жидкости (или температур окончательного расплавления твердых фаз) от состава расплава, называется линией ликвидуса. Выше линии ликвидуса – линии насыщения жидкости одной твердой фазой – на диаграмме состояния устойчивы только жидкие фазы (верхняя линия и поле, расположенное выше нее, на рис. 1, а и 2). В соответствии с принципом непрерывности линия ликвидуса плавная, без точек излома, если в системе только одна твердая фаза (см. рис. 1, а). При наличии нескольких твердых фаз в системе (см. рис. 2) на линии ликвидуса появляются точки излома, разделяющие ее на ряд ветвей и свидетельствующие об изменении числа и природы фаз. Если в системе присутствует лишь одна жидкая фаза, то число ветвей ликвидуса совпадает с числом твердых фаз, насыщающих данную жидкость. Например, вещества А и В дают одну жидкую фазу (расплав) и две твердых – кристаллы А и В. Линия ликвидуса на диаграмме состояния такой системы (рис. 3) имеет две ветви СЕ и ЕН с точкой излома «Е». Выше линии ликвидуса располагается поле I, где устойчив расплав. Ветвь ликвидуса СЕ — линия насыщения жидкости кристаллами А, а ветвь ЕН — линия насыщения расплава кристаллами В. Поэтому ниже линии СЕН размещается поле гетерогенности II и III. В каждом из них существуют две фазы — жидкая и твердая. Жидкость состава точки «Е» насыщена двумя твердыми фазами А и В. Поле существования этих двух твердых фаз и располагается ниже горизонтали ДЕF (механическая смесь). 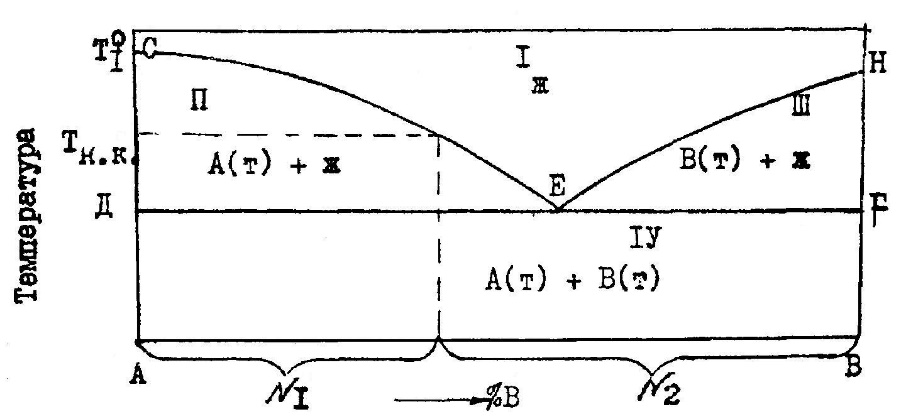 Рис. 3. Диаграмма состояния системы, компоненты которой образуют одну жидкую и две твердые фазы В системе (см. рис. 2) возможно равновесие расплава с одной из 3-х твердых фаз - раствором β, δ, γ или кристаллами химического соединения М. Поэтому на этой диаграмме три ветви ликвидуса A1E; EM1E'; E'B1, разделенные несколькими точками излома Е и E'. Линия, выражающая зависимость температур конца равновесной кристаллизации или начала расплавления твердых фаз от их состава, называется линией солидуса. Ниже линии солидуса на диаграмме состояния устойчивы только твердые фазы (см. линию ДЕF и поле ниже нее на рис. 3 и линию A1ДFM1Д'F'B1 и поля, расположенные ниже нее, на рис. 2). 5.ХИМИЧЕСКИЕ СОЕДИНЕНИЯ И ХАРАКТЕР ИХ ПЛАВЛЕНИЯХимические соединения, как и простые чистые вещества, плавятся и кристаллизуются при одной и той же температуре, но характер их плавления может быть конгруэнтным и инконгруэнтным. Если соединение плавится конгруэнтно (без разложения), то состав образующейся жидкости совпадает с составом плавящихся кристаллов. В этом случае на диаграмме состояния (рис. 4) химическому соединению АmВn отвечает вертикаль C1C, доходящая до линии ликвидуса. Ветви ликвидуса (bC и Cd) и солидуса (mC и Cn) исходят из одной экстремальной точки «С», отвечающей температуре плавления (кристаллизации) соединения АmВn. 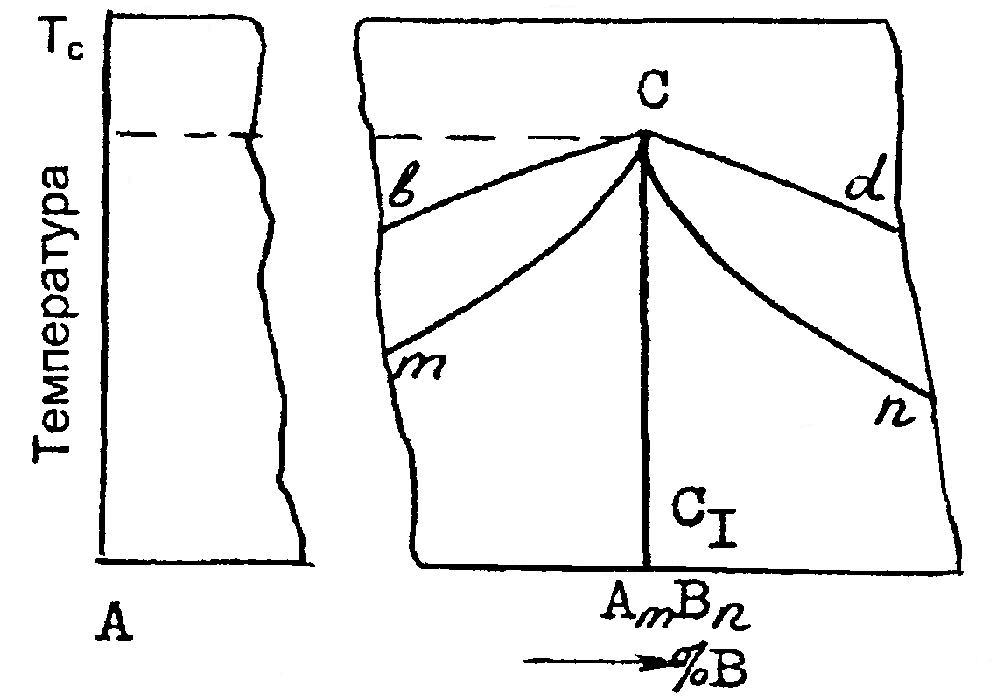 Рис. 4. Участок диаграммы состояния системы с химическим соединением АmВn плавящимся конгруэнтно Значит, если соединение плавится конгруэнтно, то на диаграмме состояния при температуре его плавления на линии ликвидуса отмечается отчетливо выраженный максимум (см. рис. 1, в и 2). При наличии в системе подобных соединений, сложные диаграммы состояния можно разделить на части, в которых химические соединения будут выполнять роль чистых компонентов. Так, систему F-К (см. рис. 1, в) можно разделить на две частные F-М и М-К, а систему А-В (см. рис. 2) на части А-М и М-В. Если соединения плавятся инконгруэнтно (с разложением), то состав образующейся жидкости не совпадает с составом плавящихся кристаллов. В таком случае при температуре плавления происходит распад химического соединения на две фазы – жидкую и твердую, например кристаллы А и жидкость точки PC (см. рис. 5)
Равновесию трех фаз на диаграмме состояния удовлетворяет горизонтальная линия. До нее и будет доходить вертикаль, отвечающая химическому соединению. А линия ликвидуса пройдет выше этой горизонтали (рис. 5) и на ней в точке, отвечающей составу химического соединения, нет максимума. 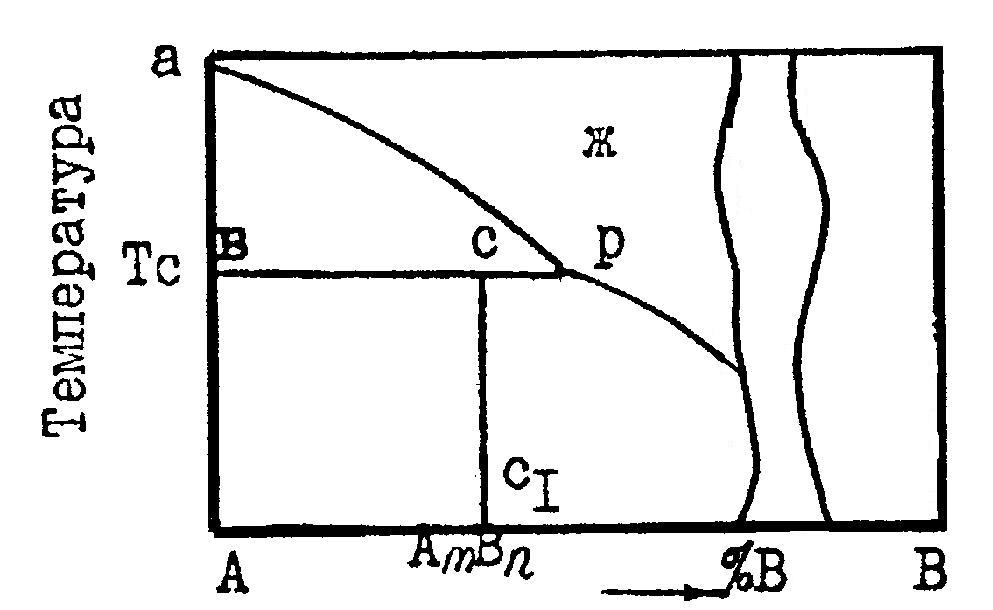 Рис. 5. Участок диаграммы состояния системы с химическим соединением АmВn, плавящимся инконгруэнтно 6. ПОЛЯ ГЕТЕРОГЕННОСТИ И ПРАВИЛО ОТРЕЗКОВРассмотрим простейшую диаграмму состояния системы, в которой металлы не обладают полиморфизмом и неограниченно растворимы друг в друге, как в жидкой, так и в твердой фазе(рис.6.). В этом случае на диаграмме всего три поля, разделенных двумя наклонными линиями. Два из них — поля гомогенности или поля существования насыщенных растворов — жидкого (поле I) и твердого (поле II). В поле гетерогенности (III) устойчивы две фазы. Обе линии диаграммы — ликвидуса (верхняя) и солидуса (нижняя) — не имеют точек излома, так как в системе всего одна твердая фаза (твердый раствор). 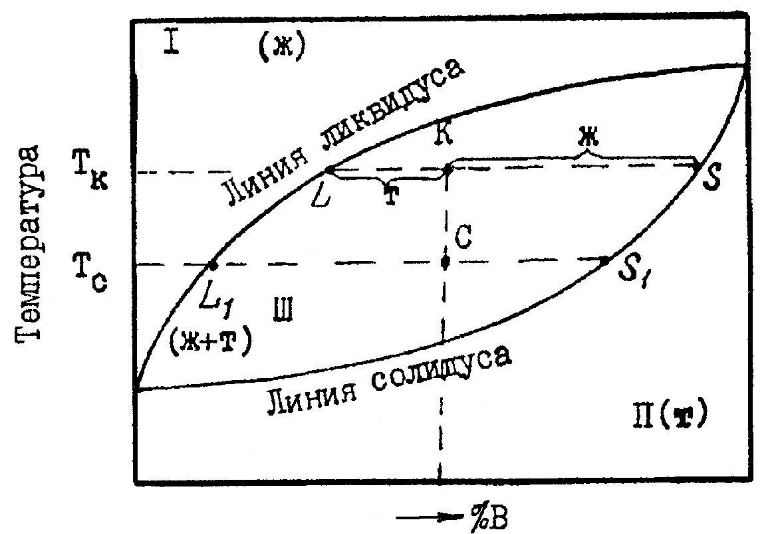 Рис. 6. Диаграмма состояния системы, компоненты которой неограниченно растворимы как в жидкой, так и в твердой фазе Любая точка внутри поля гетерогенности, например, точка «k», указывает температуру и состав смеси двух фаз. При заданной температуре (Тк) система безвариантная (С=0). Это означает, что независимо от соотношения в количествах равновесных фаз их составы определяются однозначно, им отвечают точки на линиях насыщения: точка «L» на линии ликвидуса указывает состав расплава, а точка «S» на линии солидуса — состав твердой фазы. Согласно правилу отрезков (рычага), точка «k», отвечающая составу смеси двух фаз, делит отрезок LS на части, обратно пропорциональные их количествам. Если составы на диаграмме состояния выражены массовыми процентами, то отрезок LК пропорционален массе твердой фазы (mT), а отрезок КS — массе жидкости (mЖ), и правило отрезков примет вид:
Если же составы выражены мольными процентами, то отрезки LK и KS будут пропорциональны числу молей твердой (nT) и жидкой (nЖ) фаз соответственно, и правило отрезков запишется в виде:
В двухфазной системе изменение температуры вызывает изменение составов фаз и, следовательно, соотношений в их количествах. Например, у системы, заданной точкой «k» (см. рис. 6), понизим температуру от Тk до Тс. При этом состав жидкости изменится от «L» до «L1», а состав твердой фазы от «S» до «S1» а также изменится длина отрезков, пропорциональных количествам жидкой и твердой фаз. В рассмотренном примере увеличивается доля кристаллов и уменьшается доля жидкости. Правило отрезков применимо к гетерогенным системам и, следовательно, в пределах любого поля гетерогенности. 7. ЛИНИИ БЕЗВАРИАНТНЫХ РАВНОВЕСИЙ И ИЗОТЕРМИЧЕСКИЕ ПРЕВРАЩЕНИЯ С УЧАСТИЕМ ТРЕХ ФАЗЛюбая горизонтальная линия диаграммы отвечает безвариантному равновесию трех конденсированных фаз. При внешнем воздействии на подобную систему (подводе или отводе тепла) равновесие смещается и возникает самопроизвольно протекающий процесс, при котором ни температура, ни составы фаз изменяться не могут (С=0). Такие изотермические превращения с участием трех конденсированных фаз протекают по двум схемам: а) распад одной фазы на две другие; б) взаимодействие двух фаз с образованием третьей. В качестве примера рассмотрим превращения с участием одной жидкой и двух твердых фаз, происходящие при отводе тепла от системы. 1. Эвтектическое превращение, сводящееся к одновременной кристаллизации двух твердых фаз из жидкости (схема «a»). Его можно описать следующим уравнением:
где ЖЕ – жидкость (расплава) эвтектического состава «E»; Та, Тв – твердые фазы состава точек «a» и «в» соответственно. Эвтектическому превращению на диаграмме состояния удовлетворяет горизонталь (рис. 7, а), граничные точки которой («a» и «в») указывают составы твердых фаз, а между ними располагается точка «Е» (состав жидкости). В точке «Е» должны сходиться две ветви ликвидуса, так как жидкость такого состава насыщена двумя твердыми фазами, а ветви солидуса должны подходить к точкам «a» и «в». На диаграмме (см. рис. 2) две линии эвтектического происхождения. Одна из них линия ДЕF. На ней к точке «Е», указывающей состав жидкой эвтектики, подходят ветви ликвидуса A1E и M1E. Точки «Д» и «F» указывают составы твердых фаз, к ним подходят линии солидуса A1Д и M1F. Другая линия эвтектического превращения Д'Е'F1. На ней точка «Е» отвечает составу жидкой эвтектики и точки «Д» и «F» — составам твердых фаз. 2. Перитектическое превращение, при котором жидкость перитектического состава (точка «P») взаимодействует с ранее выпавшей твердой фазой (например, состава точки «а») и дает новую твердую фазу (состава точки «в»). Такому превращению, протекающему по схеме «б», удовлетворяет уравнение
На линии перитектического превращения (рис. 7, б) граничные точки «p» и «а» (составы взаимодействующих фаз) и между ними точка «в» (состав вновь возникающей фазы). 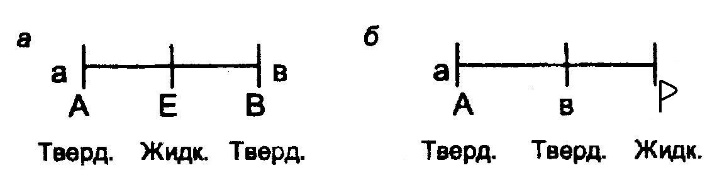 Рис. 7. Расположение составов равновесных фаз на линии эвтектического (а) и перитектического (б) превращения Такое размещение составов равновесных фаз на линиях эвтектического и перитектического превращений согласуется с правилом отрезков, по которому состав смеси двух фаз всегда располагается между составами смешиваемых фаз. На диаграмме, приведенной ранее (см. рис. 5), линия перитектического превращения ВСР. На ней к точке "р" подходит линия ликвидуса ар, точки «в» и «с» совпадают с составами твердых фаз А и АmВn соответственно. Таким образом, линии эвтектического и перитектического превращений отличаются местоположением состава жидкой фазы. Состав жидкой эвтектики располагается между составами твердых фаз, а состав жидкой перитектики находится по одну сторону от составов твердых фаз. Возможные превращения с участием трех конденсированных фаз и уравнения, их описывающие, приведены в табл. 2. Таблица 2 Возможные изотермические превращения с участием трех конденсированных фаз
Из табл. 2 видно, что монотектическое и эвтектоидное превращения протекают по такой же схеме, как и эвтектическое (схема «а»),только в первом участвуют две. жидких фазы и одна твердая, а во втором — все три фазы твердые. Аналогом перитектического превращения являются синтетическое и перитектоидное, им удовлетворяет схема «б». 8. ИЗМЕНЕНИЕ ФАЗОВОГО СОСТОЯНИЯ СПЛАВАС помощью диаграммы состояния можно проследить, какие фазовые изменения претерпевает сплав определенного состава при понижении или повышении температуры. Например, при рассмотрении кристаллизации и последующего охлаждения сплава можно установить: 1. Температуру начала кристаллизации Тн.к.. 2. Состав и температуру первично выпадающих кристаллов. 3. Как изменяются составы жидкой и твердой фаз в процессе кристаллизации. 4. Каково соотношение между относительными количествами жидкости и кристаллов в ходе кристаллизации. 5. Температуру конца кристаллизации Тк.к. 6. Какие превращения претерпевает сплав при охлаждении ниже Тк.к, а также состав и количество продуктов кристаллизации. 7. Вид кривой охлаждения. Проследим за изменением фазового состояния сплава состава точки «х» в системе А-М (рис. 8), которая представляет собой левую часть диаграммы, изображенной на рис. 2. Чтобы диаграмму не очень перегружать обозначениями, на рис. 8 отмечены лишь поля гомогенности. При температуре точки «х» заданная система, представляющая собой расплав (Ф=1), двухвариантная, и отвод тепла от нее вызовет лишь охлаждение жидкости неизменного состава до температуры. На кривой охлаждения (рис. 8, б) этому отвечает участок аb. Температура начала кристаллизации Тн.к сплава на диаграмме состояния определяется точкой пересечения вертикали исходного сплава ХХ1 с ветвью ликвидуса А1Е (линией насыщения жидкости одной твердой фазой). На кривой охлаждения этой температуре соответствует точка излома «в». С появлением твердой фазы система становится одновариантной. Поэтому при дальнейшем отводе тепла ее температура падает, но охлаждение замедляется, так как двухфазное равновесие
смещается вправо (в сторону выделения тепла). Одна степень свободы означает, что составы равновесных фаз (жидкой и твердой) зависят от температуры и определяются точками пересечения изотермы с ветвями ликвидуса и солидуса соответственно. Так, при температуре начала кристаллизации Тн.к= ТL1 состав расплава указывает точка «TL1», а состав кристаллов — точка «S1». Последняя находится на линии, ограничивающей поле гомогенности β-фазы. Поэтому первичным продуктом кристаллизации сплава «X» является одна твердая фаза – β — твёрдый раствор. По мере понижения температуры в ходе кристаллизации состав жидкости изменяется по ветви ликвидуса от «L1» до «L2» а состав твердой фазы — по ветви солидуса от «S1» до «S2», что на рис. 8, а отмечено стрелками. При температуре точки «k» в равновесии существуют две фазы — жидкая состава «L» и твердая состава «S». Соотношение в их количествах можно определить с помощью правила отрезков. Отрезок КS пропорционален массе жидкости, а отрезок КL — массе кристаллов. 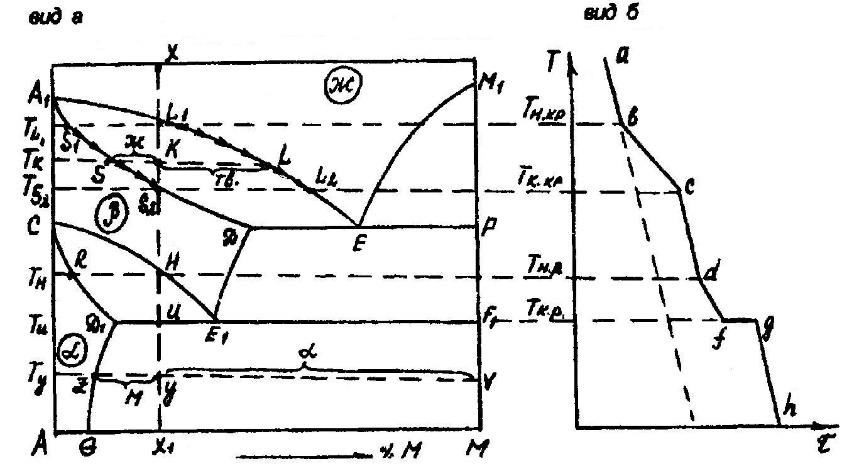 Рис. 8. Диаграмма состояния системы А-М (а) и вид кривой охлаждения сплава «х» (б) Температура конца кристаллизации сплава Тк.к= TS2 на диаграмме состояния определяется точкой пересечения вертикали XX1 с ветвью солидуса A1Д. На кривой охлаждения ей отвечает точка излома «с». По завершении кристаллизации прекращается выделение тепла, и охлаждение системы ускоряется. После исчезновения жидкости система вновь становится двухвариантной и дальнейшее охлаждение β-раствора происходит без изменения его состава. При температуре Тн β-твердый раствор становится насыщенным, из него происходит диффузное выделение α-раствора.
Процесс (7) экзотермичен, поэтому охлаждение системы вновь замедлится и при температуре начала распада твердого раствора Тн.р на кривой охлаждения отметится точка излома «d». По мере дальнейшего понижения температуры составы равновесных фаз будут изменяться по линиям насыщения: HE1 для β-раствора и RД1 для α- раствора. При температуре ТИ= Тel происходит эвтектическое превращение (диффузный распад β-твердого раствора на кристаллы вещества М и α-раствор).
Трехфазная система безвариантная. Отвод тепла от нее смещает равновесие (8) вправо. За счет теплоты, выделяющейся в результате превращения, температура в системе сохраняется неизменной (участок fg на кривой охлаждения). Лишь после исчезновения β-раствора появляется степень свободы и возможно дальнейшее понижение температуры (см. рис. 8, б, участок gh) и изменение составов фаз по линиям Д1G и F1M (см. рис. 8, а). Конечными продуктами кристаллизации сплава «X» являются две твердые фазы — вещество М и α-раствор. При любой температуре ниже ТЕL можно определить состав раствора и соотношение в количествах равновесных фаз. Например, при Ту в равновесии с кристаллами вещества М присутствует α-раствор состава точки «Z». Долю каждой из фаз найдем с помощью правила отрезков:
По теме «Фазовые равновесия» выполняется расчетно-графическое задание, которое включает 3 задачи: 1. Анализ однокомпонентной системы на примере диаграммы состояния железа. 2. Расчет ветвей ликвидуса и определения теплоты плавления чистых компонентов в двухкомпонентной системе. 3. Физико-химический анализ двухкомпонентной диаграммы плавкости. Формулировка задания и исходные данные приводятся ниже. Для облегчения выполнения задания даны приложения 1-5, библиографический список и приложение, содержащие диаграммы состояния различных металлических систем.    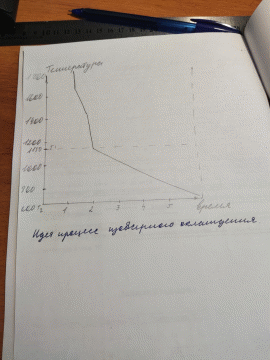     | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

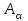
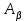
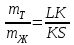 или
или 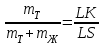
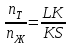 или
или 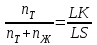
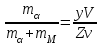 и
и