Уравнение прямой уkхв Если мы преобразуем первоначальное уравнение у у

• Название: Уравнение прямой уkхв Если мы преобразуем первоначальное уравнение у у
• Дата: 22.02.2018
• Размер: 92.99 Kb.
• Имя файла: 123.docx
• Тип: Документы; #37003

у - у₁=k(х - х₁)

уравнение прямой: у=kх+в

Если мы преобразуем первоначальное уравнение у - у₁=k(х - х₁), то получим у=kх+( у₁-kх₁) Оно удовлетворяет условия уравнения прямой : у=kх+в, т.к.

1. его степень первая, а значит оно может быть прямой,

2. прямая проходит через точку (х₁; у₁), т.к. координаты этой точки удовлетворяют уравнению : 0=0

3. роль коэфициента в играет выражение у₁-kх₁

Прямая с уравнением у - у₁=k(х - х₁) проходит через 1 точку. Потребуем, что бы и вторая точка лежала на этой прямой, т.е. что бы выполнялось равенство у₂ - у₁=k(х₂ - х₁). Отсюда находим k= у₂ - у₁¸ х₂ - х₁ и подставим в уравнение:

у - у₁ = у₂ - у₁¸ х₂ - х₁×(х - х₁) или

х - х₁¸х₂ - х₁= у - у₁¸у₂ - у₁

15.Угол м/у прямыми на плоскости

Прямые: у=k₁х +в₁, у=k₂х +в₂

В тр-ке АВС сумма внутр. углов a₁+b равна внешнему углу a₂ поэтому b=a₂-a₁Очевидно, tga₁= k₁; tga₂= k₂.Проименяя формулу для tg разности 2х углов получим tgb=tg(a₂-a₁)= tga₂-tga₁¸1+ tga₂×tga₁

Окончательно имеем tgb= k₂- k₁¸1+k_2××k₁Вычислив тангенс можно найти и сам угол b.

16. Условия || и ^ прямых на плоскости.

Даны уравнения прямых с угловым коэф. у=k₁х и у=k₂х +в₂

Условия || прямых -это равенство угловых коэф. к₁=к₂ (1)

Условие (1) выполн. и для слившихся прямых. Формулу углового коэф. прямых (tga= k₂- k₁¸1+k_2××k₁) можно записать ввиде: ctga= 1+k_2××k₁¸k₂- k₁ (это в сслучае, если к₁¹к₂). Условие ^ прямых выражается равенством k_2××k₁= -1. Если к₁=0 или к₂=0, то одна из прямых || оси Ох, а вторая ей ^, имеет уравнение вида х=а.

Пусть прямые заданы общим уравнением. А₁х+В₁у+С₁=0, А₂х+В₂у+С₂=0, Если В1=В2=0, то обе прямые параллельны оси Оу и между собой (их уравнения имеют вид х=а) Если В1=0, а В2¹0, то прямые^. В случае когда А2=0 (уравнение приводится к виду х=а, у=в)В случае В1¹0 и В2¹0можно выразить у в каждом уравнении. у= -А1х¸В1-С1¸В1;

У= - А2х¸В2-С2¸В2, тогда к1= -А1¸В1, а к2= - А2¸В2 и условие || А1¸В1= А2¸В2 или А1¸А2= В1¸В2.

С помощью равенства 1+к1×к2=0, 1+ А1¸В1× А2¸В2=0. Приходим к условию ^прямых А1×А2+В1×В2=0.

Эллипс

Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (большая расстояния между фокусами)

Уравнение элипса примет самый простой вид, если фокусы разместить на оси Ох слева от начала координат на равном от него расстоянии. F₁ F₂ - фокусы эллипса. Обозначим F₁F₂ = 2c тогда фокусы имеют координаты (-с,0) и (с,0). Расстояния о фокусов до текущей точки эллипса М обозначим r₁ и r₂. Их называют фокальными радиусами. Постоянную величину r₁ + r₂ обозначим 2а: r₁ + r₂ =2а. помещая точку М в точки и А' легко сообразить, что А'А = 2а. Отрезки AA' и ВВ' называются осями эллипса, а отрезки ОА и ОВ - полуосями эллипса. Точки А,А',В,В' называют вершинами эллипса. Пусть М(х,у)находится в точке В, тогда r₁ = r₂ =а. Из тр-ка ВОF₂ ВО=ÖBF₂²-OF₂² Обозначим ВО=в, тогда в=Öа² - с² . Через полуосиэллипса а и в уравнение запишится так:

 Это уравнение называют каноническим уравнением эллипса. Окружность - частный случай эллипса, получается при а=в=R(R - радикс окружности). Чем больше отличаются друг от друга полуоси а и в, тем более сплюснутым будет эллипс. Степень сплюснутости эллипса принято измерять эксцентриситетом 

Очевидно, 0£ɛ£1. При ɛ=0 имеем окружность, с увеличением ɛэллипс все больше отличается от окружности, становясь более выпуклым.

Гипербола

Гиперболой называется геом. место точек плоскости , для которых абсолютная величина разности расстояний до двух данный точек, называемых фокусами, есть величина посоянная, не равная 0 и меньшая расстояния между фокусами. Фокусы F₁ и F₂ снова расположим на оси Ох в точках (-с,0), (с,0). Отрезки F₁М = r₁ и F₂М = r₂ называют фокальными радиусами. По определению |r₁ - r₂ | есть величина постоянная. Обозначим ее 2а: |r₁ - r₂| =2а. Точки А и А' называют вершинами гиперболы. Легко понять, что АА' =2а. Действительно, для точки А r₁ =АF₁ а r₂ =АF₂. Очевидно, АF₂=А'F₁,поэтому r₁ - r₂ = АF₁-АF₂= АF₁=А'F₁ = А'A. С другой стороны r₁ - r₂ =2а. Отрезок АА' называют действительной осью гиперболы. Пусть в=Öс²-а² Точки В и В' имеют координаты(0,в) и (0,-в). отрезок ВВ' называют мнимой осью гиперболы. Канонической уравнение гиперболы имеет вид:

у гиперболы 2 ветви, при а=в гиперола называется равнобочной. Уравнения у=вх¸а и у=-вх¸а. Они называются асимптотами. Если точка удаляется по любой из ветвей гиперболы, то ее расстояние до соответствующей асимптоты стремиться к 0. Для гиперболы эксцентриситет  принимает зн-ия большие 1.

 

Парабола.

Параболой называется геометрическое место точек плоскости, равноудаленных от данной прямой, называемой директрисой, и от данной точки, не принадлежащей директрисе, называемой фокусом. Обозначим расстояние между фокусом и директрисой через р. Канонической уравнение параболы имеет вид:

у²=2рх и получается, если фокус F поместить в точку (р¸2, 0), а в качестве директрисы взять прямую х = - р¸2. Число р называют параметром параболы, точку (0,0) - ее вершиной.

20. Плоскость в пространстве: общее уравнение, геометрический смысл коэфициентов, уравнение плоскости., проходящей через заданную точку пространства.

Общее уравнение плоскости: Ах+Ву+Сz +D=0, в котором хотя бы один из коэффициентов А,В,С отличен от 0. Эти коэффициенты имеют опред. Геом. смысл

 

Зададим положение плоскости с помощью некоторой точки М₀(х₀,у₀,z₀) и ненулевого вектора N(А,В,С), перпендекулярного плоскости. По этим данным плоскость определяется однозначно. Пусть М(х,у,z) - текущая точка плоскости. Векторы N(А,В,С) и М₀М(х-х₀,у-у₀,z-z₀) ортогональны, поэтому их скалярное произведение равно )

А(х-х₀)+В(у-у₀)+С(z-z₀)=0 (1)

После преобразований получаем уравнение:

Ах+Ву+Сz+D=0, где D = -Ах₀-В_0-Сz₀

Следовательно, А,В,С - координаты вектора, перпендекулярного плоскости, заданной общим уравнением.

Множество плоскостей, описываемых уравнением (1), при фиксированной точке (х₀,у₀,z₀) и переменных коэфициентах А,В,С называются связкой плоскостей. Когда среди условий, задающих искомую плоскость, значится ее точка М₀(х₀,у₀,z₀), можно начинать решение задачи с применения уравнения (1). Плоскость так же называют поверностью первого порядка.

Сфера,

Сфера. Уравнение сферы, центр которой находится в начале координат: х²+у²+z²=R². Пусть теперь центр расположен в точке М₀(х₀,у₀,z₀)

Текущая точка М(х,у,z) сферы находится на расстоянии R от т. М.

Из равенства ММ₀²=R² получаем: (х-х₀)²+(у-у₀)²+(z-z₀)²=R²

Эллипсоидканонич. уравнение:

 - а,в,с - полуоси эллипсоида. При а=в получается эллипсоид вращения. Такую форму имеет поверхность нашей планеты. При а=в=с эллипсоид превращается в сферы радиуса R=а

Параболоид вращения

В плоскости уОz рассмотрим параболу у²=2рz. Поверхность, образованная вращением этой параболы вокруг оси Oz называется параболоидом вращения.

Пусть М(х,у,z) - произвольная точка поверхности, а М₀ - точка с той же аппликатой z, лежащая на параболе у²=2рz. Т.к. О'М=О' М₀, то у² для точки М₀ можно заменить в уравнении на х²+у² для точки М: х²+у²=2рz - уравнение параболоида вращения

Уравнение прямой, проходящей через две точки

Пусть прямая проходит через точки М₁ (х₁; у₁) и М₂ (х₂; у₂). Уравнение прямой, проходящей через точку М₁, имеет вид у— у₁ = k (х — х₁), (10.6)

где k — пока неизвестный коэффициент.

Так как прямая проходит через точку М₂(х₂ у₂), то координаты этой точки должны удовлетворять уравнению (10.6): у₂—у₁ = k (х₂—х₁).

Отсюда находим Подставляя найденное значениеk в уравнение (10.6), получим уравнение прямой, проходящей через точки М₁ и М₂: 

Предполагается, что в этом уравнении х₁ ≠ х₂, у₁ ≠ у₂

Если х₁ = х₂, то прямая, проходящая через точки М₁ (х₁ ,у_I) и М₂ (х₂,у₂) параллельна оси ординат. Ее уравнение имеет вид х = х₁.

Если у₂ = у_I, то уравнение прямой может быть записано в виде у = у₁, прямая М₁ М₂ параллельна оси абсцисс.

Уравнение прямой в отрезках

Пусть прямая пересекает ось Ох в точке М₁(а;0), а ось Оу – в точке М₂(0;b). Уравнение примет вид: 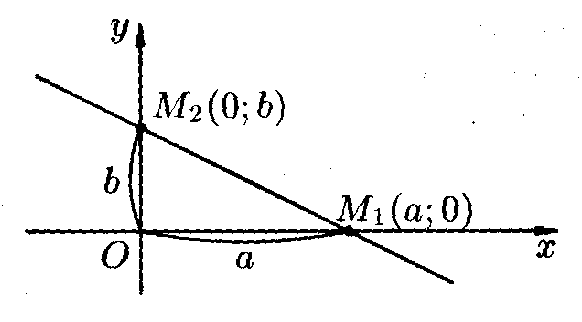т.е.. Это уравнение называетсяуравнением прямой в отрезках, т.к. числа а и b указывают, какие отрезки отсекает прямая на осях координат.



Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору

Найдем уравнение прямой, проходящей через заданную точку Мо (х_О; у_о) перпендикулярно данному ненулевому вектор n = (А; В).

Возьмем на прямой произвольную точку М(х; у) и рассмотрим вектор М₀М (х — х₀; у - у_о) (см. рис.1). Поскольку векторы n и М_оМ перпендикулярны, то их скалярное произведение равно нулю: то есть

А(х — хо) + В(у — уо) = 0. (10.8)

Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Вектор n= (А; В), перпендикулярный прямой, называется нормальным нормальным вектором этой прямой.

Уравнение (10.8) можно переписать в виде Ах + Ву + С =0, (10.9)

где А и В координаты нормального вектора, С = —Ах_о - Ву_о - свободный член. Уравнение (10.9) есть общее уравнение прямой (см. рис.2).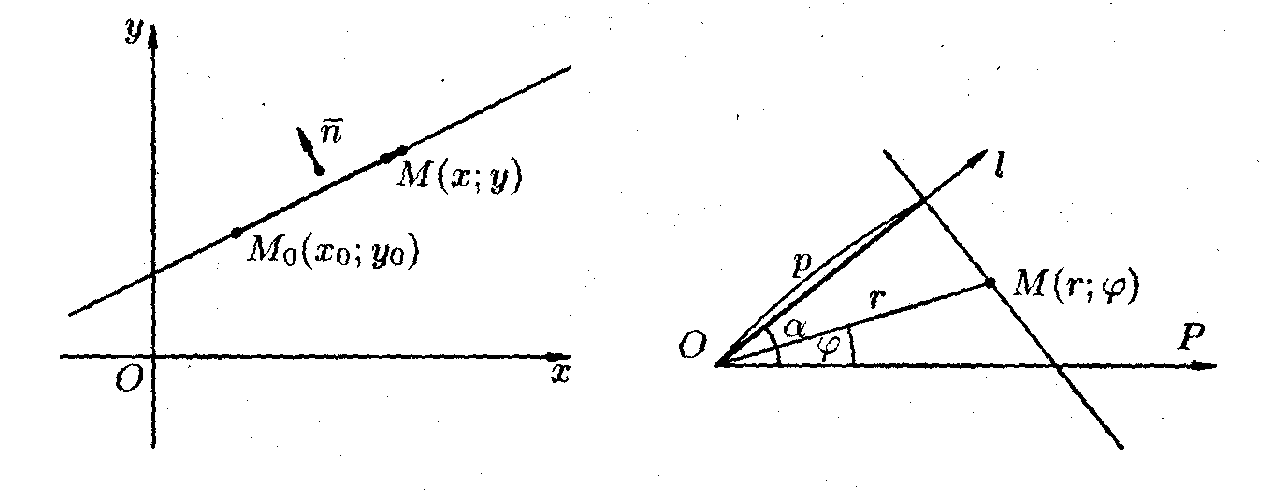



Рис.1 Рис.2

Канонические уравнения прямой

,

Где - координаты точки, через которую проходит прямая, а- направляющий вектор.

Кривые второго порядка Окружность

Окружностью называется множество всех точек плоскости, равноотстоящих от данной точки, которая называется центром.

Каноническое уравнение круга радиуса R с центром в точке :



В частности, если центр кола совпадает с началом координат, то уравнение будет иметь вид:

Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точеки, которые называются фокусами, есть величина постоянная, большая чем расстояние между фокусами.

x

Каноническое уравнение эллипса, фокусы которого лежат на оси Ох, а начало координат посредине между фокусами имеет вид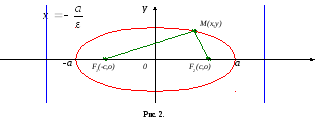гдеa длина большой полуоси; b– длина малой полуоси (рис. 2).

Зависимость между параметрами эллипса ивыражается соотношением:

(4)

Эксцентриситетом эллипса называется отношение межфокусного расстояния 2с к большой оси 2а: 

Директрисамиэллипса называются прямые, параллельные оси Оу, которые находятся от этой оси на расстоянии. Уравнения директрис:.

Если в уравнении эллипса , тогда фокусы эллипса находятся на оси Оу.

Итак,