Лабораторная работа 1. Фазовый синхронизм при генерации второй гармоники лазерного излучения в одноосных кристаллах
 Скачать 193.63 Kb. Скачать 193.63 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ(ТУСУР) Кафедра электронных приборов (ЭП) ОТЧЕТ ФАЗОВЫЙ СИНХРОНИЗМ ПРИ ГЕНЕРАЦИИ ВТОРОЙ ГАРМОНИКИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ В ОДНООСНЫХ КРИСТАЛЛАХ Лабораторная работа №1 по дисциплине «Когерентная оптика и голография»
Томск 2021 1 ВВЕДЕНИЕ Цель настоящей работы является исследование фазового синхронизма в отрицательных одноосных нелинейных кристаллах. 2 ОСНОВНЫЕ РАССЧЕТНЫЕ ФОРМУЛЫ Показатель преломления обыкновенной волны рассчитывается по следующей формуле: 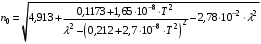 (2.1) (2.1)где 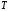 – температура; – температура; – длина волны. – длина волны.Показатель преломления необыкновенной волны рассчитывается по следующей формуле: 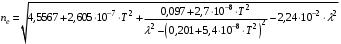 (2.2) (2.2)Угол синхронизма рассчитывается по следующей формуле: 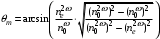 (2.3) (2.3)где 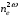 – показатель преломления необыкновенной волны на длине волны второй гармоники; – показатель преломления необыкновенной волны на длине волны второй гармоники;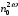 – показатель преломления обыкновенной волны на длине волны второй гармоники; – показатель преломления обыкновенной волны на длине волны второй гармоники;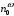 – показатель преломления обыкновенной волны на основной длине волны. – показатель преломления обыкновенной волны на основной длине волны. Показатель преломления необыкновенной волны в зависимости от угла рассчитывается по следующей формуле 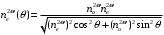 (2.4) (2.4)Волновая расстройка рассчитывается по следующей формуле: 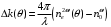 (2.5) (2.5)Выходная мощность пучка второй гармоники рассчитывается по следующей формуле:  (2.6) (2.6)где 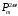 – амплитуда выходной мощности пучка второй гармоники; – амплитуда выходной мощности пучка второй гармоники;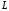 – длина кристалла. – длина кристалла.Внутренний угол синхронизма вычисляется по следующей формуле: 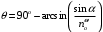 (2.7) (2.7)где 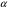 – угол измеренный относительно нормали к поверхности кристалла. – угол измеренный относительно нормали к поверхности кристалла. Нормированная интенсивность вычисляется по следующей формуле: 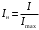 (2.8) (2.8)где  – измеренная интенсивность; – измеренная интенсивность; 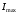 – максимальная измеренная интенсивность. – максимальная измеренная интенсивность.3 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ Схема лабораторной установки, используемой в настоящей работе, схематично изображена на рис. 3.1. В данной работе в качестве источника накачки при изучении генерации второй гармоники используется твердотельный лазер 1 с диодной накачкой, типа LCS-DTL-324QT, работающий в импульсно-периодическом режиме на длине волны 1,064 мкм. Длительность импульса составляет 10 нс, а частота повторения может варьироваться от 100 Гц до 10 кГц. Излучение накачки, имеющее вертикальную поляризацию, проходит через нелинейный кристалл ниобата лития 2, выращенный из расплава стехиометрического состава. Кристалл расположен на нагревателе 6, в качестве которого используется модуль Пелтье, подключенный к регулируемому источнику тока. Температура кристалла измеряется термопарой и цифровым мультиметром, которые на рис. 1.1 не показаны. Оптическая ось Z кристалла расположена в плоскости рисунка, а сам он вместе с нагревателем может вращаться по углу в этой плоскости благодаря столику 7 с микрометрическим винтом. Угол падения пучка накачки на входную грань кристалла, нормаль к которой ортогональна его оптической оси Z, измеряется при повороте столика по угломерной нониусной шкале. При некоторых углах падения, близких к углу синхронизма, в кристалле генерируется пучок с частотой второй гармоники, распространяющийся в одном направлении с пучком накачки. После дисперсионной призмы 3 эти пучки разделяются по углу, и мощность пучка накачки измеряется с помощью фотодиода 4 типа ФД-24К, по генерируемому фототоку, цифровым мультиметром 5. 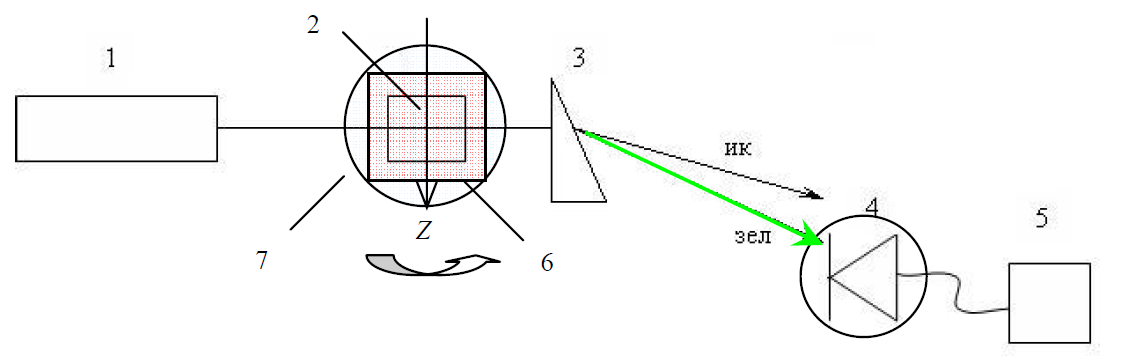 Рисунок 3.1 – Схема экспериментальной установки для исследования фазового синхронизма при ГВГ в одноосном нелинейном кристалле; 1 – твердотельный лазер; 2 – кристалл ниобата лития; 3 – дисперсионная призма; 4 – фотодиод ФД-24К; 5 – цифровой мультиметр; 6 – модуль Пелтье; 7 – поворотный столик с микрометрическим винтом и угломерной шкалой 4 ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ Вычислим по формулам (2.1) и (2.2) показатели преломления для обыкновенной и необыкновенной волн двух гармоник в среде MathCad: 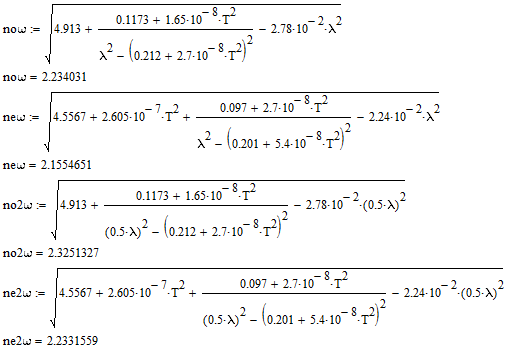 Вычислим по формуле (2.3) угол синхронизма:  Вычислим по формуле (2.4) показатель преломления необыкновенной волны: 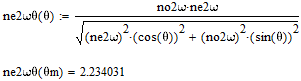 Для получения кривой углового синхронизма, в среде MathCad, написана программа с использованием формул (2.5) и (2.6), вычисляющая мощность выходного излучения второй гармоники, примем также что 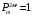 . . Результат работы программы представлен на рис. 4.1. 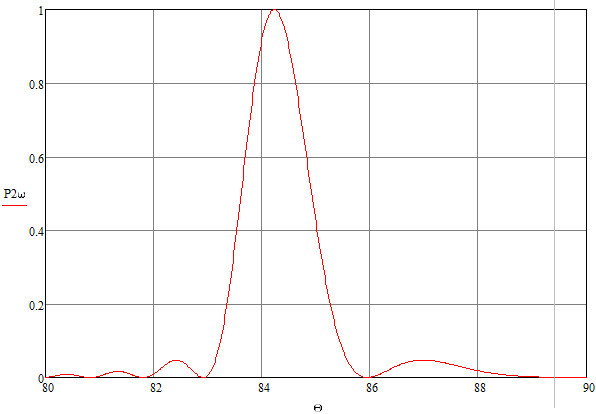 Рисунок 4.1 – Теоретическая кривая углового синхронизма. В таблице 4.1 представлены экспериментальные данные полученные в ходе снятия кривой синхронизма. Таблица 4.1 – экспериментальные данные.
Вычислим по формуле (2.7) угол внутри кристалла:  . .Аналогично вычислим другие значения и занесем их в таблицу 4.1. Вычислим по формуле (2.8) нормированную интенсивность, в нашем случае 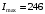 : :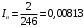 . .Аналогично вычислим другие значения и занесем их в таблицу 4.1. На рис. 4.2 представлена зависимость нормированной интенсивности второй гармоники выходного пучка от угла. 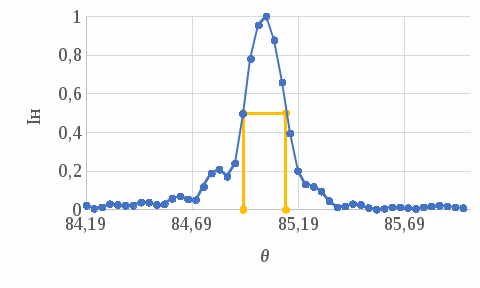 Рисунок 4.2 – Зависимость нормированной интенсивности второй гармоники выходного пучка от угла. Угол синхронизма составляет: 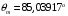 . .Вычислим ширину синхронизма по уровню 0,5. Для этого, на рис. 4.2 опустим перпендикуляры на ось 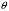 , так чтобы они пересекали кривую в точках равных 0,5. Получены следующие значения: , так чтобы они пересекали кривую в точках равных 0,5. Получены следующие значения: 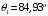 , , 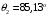 . Ширина синхронизма составляет: . Ширина синхронизма составляет: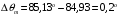 . .5 ЗАКЛЮЧЕНИЕ В ходе данной работы написана программа в MathCad, рассчитывающая мощность выходного пучка второй гармоники и для получения теоретической кривой углового синхронизма, также снята экспериментальная кривая углового синхронизма. Теоретический угол синхронизма составляет: 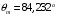 . .Экспериментальный угол синхронизма составляет: 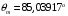 . .Ширина синхронизма составляет: 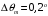 . . |
