Задача 1. Вычислить теплоемкость единицы объема кристалла бромистого алюминия AlBr3 по классической теории теплоемкости. Определить теплоту, необходимую для нагревания кристалла AlBr3 массой 10 г на Т=5К. ОТВЕТ: Q 18,7Дж
AlBr3
m = 10 г
Т=5К
|
Решение:
Темплоемкость единицы объема кристалла можно определить по формуле
С = Сm/Vm
где Сm и Vm теплоемкость и объем одного моля вещества. Молярная теплоемкость определяется по закону Неймана-Коппа
Сm=3nR , где n - число атомов в соединении. Для AlBr3 n = 4. Объем Vm можно выразить через плотность кристалла
Vm = m/r.
Масса моля AlBr3 равна
m = 3mBr + mAl.
Подставим эти выражения в расчетную формулу для теплоемкости
С = 12Rr/(3mBr+mAl).
Из таблицы находим плотность этого кристалла r = 3,01 103кг/м3, mBr = 80 г/моль; mAl = 27 г/моль. С учетом этих значений теплоемкость
 = =  Дж/м3К Дж/м3К
Теплота DQ, необходимая для нагревания тела от Т1 до Т2, может быть вычислена по формуле
Q= dt= dt=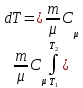 T T
поскольку по классической теории молярная теплоемкость не зависит от температуры. Тогда окончательно:
Q=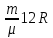 T = T = =18.7Дж =18.7Дж
Ответ: Q 18,7Дж
|
Найти:
Q ?
|
Задача 2: Пользуясь теорией теплоемкости Эйнштейна, определить изменение внутренней энергии одного килоатома кристалла при нагревании его от Т1=0 до Т2=0,1Е. Характеристическую температуру Эйнштейна Е принять для данного кристалла равной 300 К. ОТВЕТ: 340 Дж.
Дано:
Т1=0
Т2=0,1Е
Е=300 К
|
Решение:
Внутренняя энергия одного атома кристалла в квантовой теории теплоемкости Эйнштейна может быть определена по формуле:
U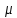 = U = U
Изменение внутренней энергии:
U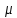 = =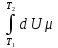 = =
Для низких температур (Т<Е) теплоемкость определяется по формуле:
Сm = 3R( )2exp(- )2exp(- ). ).
Подставим это выражение в выражение для внутренней энергии:
U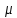 = = dT dT
Введем новую переменную х =  /Т. Тогда /Т. Тогда
dx = - ( /T2)dT, /T2)dT,
температура Т1 соответствует х1, Т2 - x2 = qЕ /0,1 /0,1 = 10. = 10.
Окончательно получим
U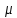 = = = =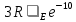 =3 =3 =340Дж =340Дж
Ответ: 340Дж
|
Найти:
σ-?
Е-?
| |
 Скачать 17.9 Kb.
Скачать 17.9 Kb.
 =
=  Дж/м3К
Дж/м3К dt=
dt=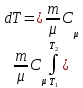 T
T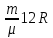 T =
T = =18.7Дж
=18.7Дж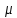 = U
= U
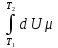 =
=
 )
) dT
dT /Т. Тогда
/Т. Тогда  =
=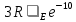 =3
=3 =340Дж
=340Дж