Определение коэффициента трения качения методом наклонного маятника
 Скачать 145.5 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет» Архитектурно-строительный институт Кафедра «Прикладные и естественнонаучные дисциплины» Отчет принят__________________________ Оценка_______________________________ Преподаватель кафедры ПЕД Маскова А.Р. ________________________________Ф.И.О. Лабораторная работа № 2-4 «Определение коэффициента трения качения методом наклонного маятника» Выполнил ст. гр. БВТ 20-01 А.С. Алешин Уфа 2020 Цель работы: определение коэффициента трения качения различных материалов. Приборы и принадлежности: наклонный маятник, штангенциркуль, шары, пластины. Описание установки: 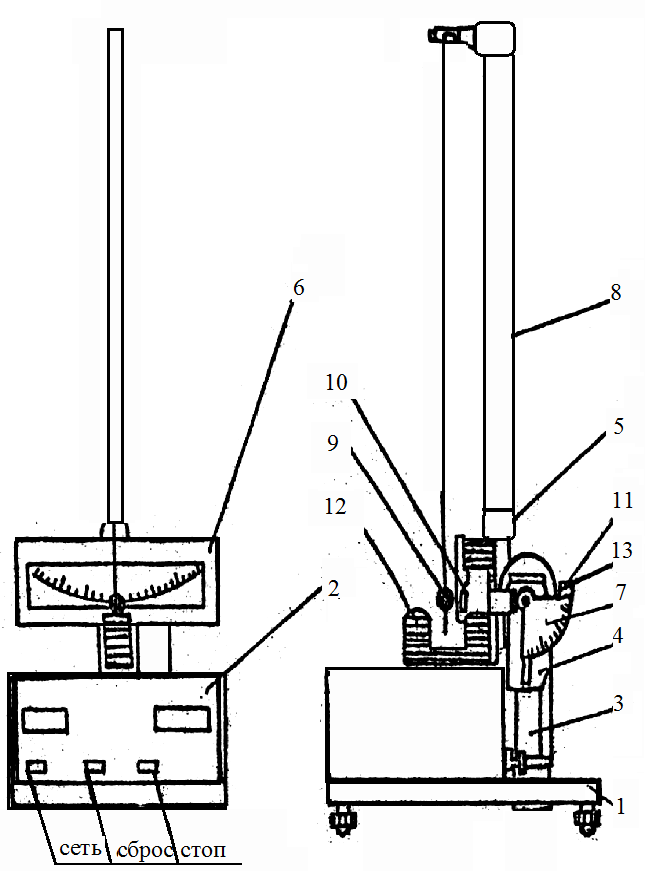 1-плита с опорными винтами 2-секундомер FRM-142 3-труба 4-корпус 5-держатель 6-шкала отклонения шара 9 7-шкала наклона трубы 3 8-кронштейн 9-шар 10-образец 11-маховичок 12-фотоэлектрический датчик 13-винт Вывод расчетной формулы: Расчетную формулу для определения коэффициента трения качения можно вывести на основании закона сохранения энергии. Пусть ∆Е – уменьшение энергии маятника после некоторого числа колебаний, обусловленное их затуханием. Энергия ∆Е расходуется на работу силы трения качения ∆А на деформацию нити ∆А/ . Но работа ∆А/ очень мала и ев можно пренебречь. Тогда получаем ∆Е = ∆А. (1) ∆Е= П0 - Пп = Р ∙∆h, (2) Где Пп – его потенциальная энергия в конечном крайнем положении. ∆h – разность высот центра тяжести колеблющегося тела в начальном и конечном крайних положениях по отношению к произвольно набранному горизонтальному уровню. П0– потенциальная энергия в конечном начальном положении ∆h = ∆x sinβ =l (cosφn- cosφ0) sinβ(3) где l – длина маятника. Подставим (3) в (2) и получим: ∆E = P l sinβ (cosφn - cosφ0).(4) ∆A =Fкач∙S(5) S = S0 + 2S1 + 2S2 +…+ 2Sn-1 + Sn = S0 + Sn +2(S1 + S2 + Sn-1).(6) Так как амплитуда S0, S1, S2, …Sn убывает по закону арифметической прогрессии, то можно записать.  (7)S1 = S0 - ∆S; Sn-1 = Sn + ∆S Выражая S1 и Sn-1, можно записать S1 +Sn-1 = S0 – ∆S +Sn +∆S = S0 + Sn.(8) Объединяя (7) и (8) получаем в (6):  .(9)Амплитуда S0 и S1 представляет собой дуги окружности радиуса l , поэтому S0 =l φ0 ; Sn =l ∙ φn , (10)
Таким образом, путь, пройденный маятником за n простых колебаний, как следует из выражений (9) и (10), равен  ; . (11) Сила трения качения определяется как  (12)
 (13)Подставляя выражение (13) и (11) в (5), получим работу силы трения, совершенную за z полных колебаний:  (14)Решая уравнения (4) и (14) получим  . (15)Принимая во внимание, что углы φ0 и φn, стоящие в знаменателе этой формулы, должны быть выражены в радианах, а наклонный маятник снабжен для этих углов градусной шкалой, можно вывести переводной коэффициент. Учитывая, что I0 =1/57,3 рад. Получим окончательную формулу  . (16) Определение погрешностей: 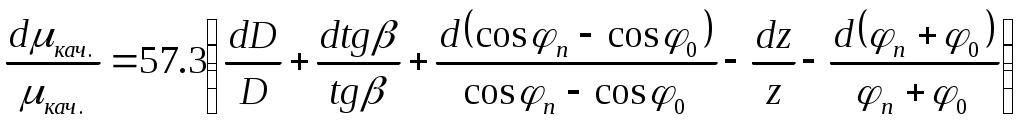 ; ;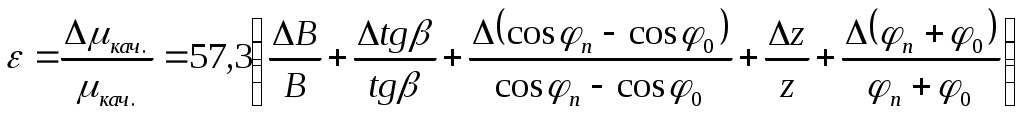 – относительная ошибка : – абсолютная ошибка.Окончательный результат запишем в виде:  .Результаты измерений
|
. P2 = P cos β с учетом этого выражения (12) примет следующий вид:
мм