Пракраб Менеджм. Федеральное агентство морского и речного транспорта Федеральное государственное бюджетное образовательное учреждение высшего образования Государственный университет морского и речного флота имени адмирала С. О. Макарова

• Название: Федеральное агентство морского и речного транспорта Федеральное государственное бюджетное образовательное учреждение высшего образования Государственный университет морского и речного флота имени адмирала С. О. Макарова
• Дата: 13.12.2022
• Размер: 2.3 Mb.
• Имя файла: Пракраб Менеджм.doc
• Тип: Практическая работа; #842492

Федеральное агентство морского и речного транспорта

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Государственный университет морского и речного флота

имени адмирала С.О. Макарова»

Институт международного транспортного менеджмента

Кафедра менеджмента на водном транспорте

Практические работы
по дисциплине «Менеджмент»

Направление подготовки 38.03.01 Экономика
Выполнила студентка группы Э-4 ЗО

Семенова А.Ю.

Вариант №12
Проверила: профессор кафедры

Менеджмента на водном транспорте

доцент, к.т.н. О.А. Туаршева


Санкт-Петербург

2022
Практическая работа № 1
Определение оптимальной расстановки судов по причалам и оптимальной очередности их обработки

Постановка задачи

В работе необходимо решить три задачи:

• 
  Оптимальная расстановка пяти разных судов к пяти взаимозаменяемым причалам разной пропускной способности.
  
• 
  Выбор оптимальной очередности обработки пяти судов на одном причале с известной пропускной способностью.
  
• 
  Выбор оптимальной очередности обработки пяти судов при их двух операционном обслуживании в порту, например, при разгрузке каждого судна на причале выгрузки и погрузки каждого на другом причале.
  

Исходные данные

Перечень из пяти причалов с указанием их пропускных способностей Пj, т/сут (для решения первой задачи) для всех студентов задается одинаковым:

П₁ = 3500 т/сут.,

П₂ = 2800 т/сут.,

П₃ = 5200 т/сут.,

П₄ = 1900 т/сут.,

П₅ = 2300 т/сут.

Перечень из пяти судов (таблица 1) с указанием их грузоподъемности (загрузки) Gi, т для решения первой и второй задачи. Считаем, что загрузка судов равна их грузоподъемности.

Таблица 1

№ п/п	Проект судна	Грузоподъемность (загрузка судна) Gi, т	Себестоимость содержания судна на стоянке Сi, у.е. / сут
1	006RSD05	4800	120
2	8203	5150	240
3	RSD19	3800	200
4	005RSD03	7000	320
5	KWC360	5000	480

Причал с пропускной способностью Пj, т/сут (для решения второй задачи). Задается один из пяти причалов из первой задачи – причал № 2 =2800 т/сут.

Время выгрузки и погрузки каждого судна у причалов при их двух операционной обработке (для решения третьей задачи) tij, ч (сут) (таблица 2) Себестоимость содержания судов на стоянке Сi, руб. / сут (таблица 1).

Таблица 2

Номер	Время, ч.
	Выгрузки	Погрузки
1	12	20
2	13	25
3	14	12
4	11	33
5	9	24

Решение задачи

1. 
   Критерий выбора оптимальной расстановки судов по причалам — суммарные эксплуатационные расходы по стоянке судов — определяем по формуле:
   

Σ Ci ti = Σ (Сi Gi  /  Пj) → min.

Для определения оптимальной расстановки судов по причалам используется правило Е. Е. Архипова: к причалу с большей производительностью необходимо ставить судно, у которого показатель Сi Gi больше, а следовательно:

Таблица 3

Оптимальная расстановка судов по причалам

№ п/п	Проект судна	Грузоподъем-ность (загрузка судна) Gi, т	Себестоимость содержания судна на стоянке Сi, у.е. / сут	Сi Gi	Номер причала	Пропускная способность причала, Пj, т / сут
1	006RSD05	6600	160	1 056 000	5	2300
2	8203	7200	240	1 728 000	1	3500
3	RSD19	6528	200	1 305 600	2	2800
4	005RSD03	5200	400	2 080 000	3	5200
5	KWC360	4500	120	540 000	4	1900

Примеры решения

1. 
   Показатель СiGi:
   

• 
  С₁ G₁ =6600*160 = 1 056 000
  
• 
  С₂ G₂ =7200*240 = 1 728 000
  
• 
  С₃ G₃ = 6528*200 = 1 305 600
  
• 
  С₄ G₄ = 5200*400 = 2 080 000
  
• 
  С₅ G₅ = 4500*120 = 540 000
  

2. 
   Суммарные эксплуатационные расходы:
   

Σ C_it_i= 1056000/2300+1728000/3500+1305600/2800+2080000/5200+540000/1900= 459,13+493,71+466,29+400,00+284,21=2 103,34 у.е.

Вывод: с помощью правила Е.Е. Архипова, получены минимальные суммарные эксплуатационные расходы 5 судов на 5 причалах.

2. 
   Критерием выбора оптимальной очередности обработки судов на причале служат затраты времени или расходы по содержанию судов на простое.
   

В первую очередь следует поставить под обработку то из судов, у которого значение С_i/ t_iбудет большим.

Расчет t_iнужно выполнять по формуле t_i= G_i/ П.

Решение задачи оформляется в виде таблице 4.
Таблица 4

Оптимальная очередность обработки судов

№ п/п.	Проект судна	Грузоподъемность (загрузка судна) Gi, т	Себестоимость содержания судна на стоянке Сi, руб. / сут	Срок обработки судна ti, сут	Сi / ti	Оптимальная очередность
1	006RSD05	6600	160	2,357	67,883	5
2	8203	7200	240	2,571	93,349	2
3	RSD19	6528	200	2,331	85,800	3
4	005RSD03	5200	400	1,857	215,401	1
5	KWC360	4500	120	1,607	74,667	4

Примеры решения

t₃= G₃/ П = 6528/2800=2,331 сут.

t₅= G₅/ П = 4500/2800=1,607 сут.
С₃/t₃ =200/2,331 = 85,800 у.е./сут.

С₅/t₅ =120/1,607 = 74,673 у.е./сут.
Вывод: получена оптимальная очередность обработки 5 судов на причале № 2:

- в первую очередь под обработку ставим судно 005RSD03;

- во вторую – 8203;

- в третью - RSD19;

- в четвертую - KWC360;

- в пятую - 006RSD05
3. Оптимальная очередность обработки судов при их двух операционном обслуживании в порту устанавливается на основе «Теории расписания», которая в качестве критерия оптимальности рассматривает сокращение времени ожидания судами операций обработки

В двух столбцах перечисляются все затраты времени по i-му судну на причалах I и II (первая и вторая операции): t_iI, t_iII (таблица 5).

Таблица 5

Оптимальная очередность обработки судов при двухоперационном их обслуживании

Номер	Время, ч.		Оптимальная очередность обработки
	Выгрузки	Погрузки
1	12	20	3
2	13	25	4
3	14	12	5
4	11	33	2
5	9	24	1

Выбираются минимальные из всех выписанных в обоих столбцах значений tiI и tiII.

Если минимальным оказалось какое-то из значений в первом столбце (операция разгрузки), это судно обрабатывается в первую очередь.

Если минимальным оказалось значение затрат времени во втором столбце (операция погрузки), то судно обрабатывается в последнюю очередь. Далее — аналогично.

В случае же, когда в обоих столбцах оказались равные значения времени обработки, выбор очередности обработки этих двух судов можно производить в любом порядке.
После определения оптимальной очередности обработки судов строятся графики их обработки:

1 — для заданной очередности (рис. 1);

2 — для оптимальной очередности (рис. 2).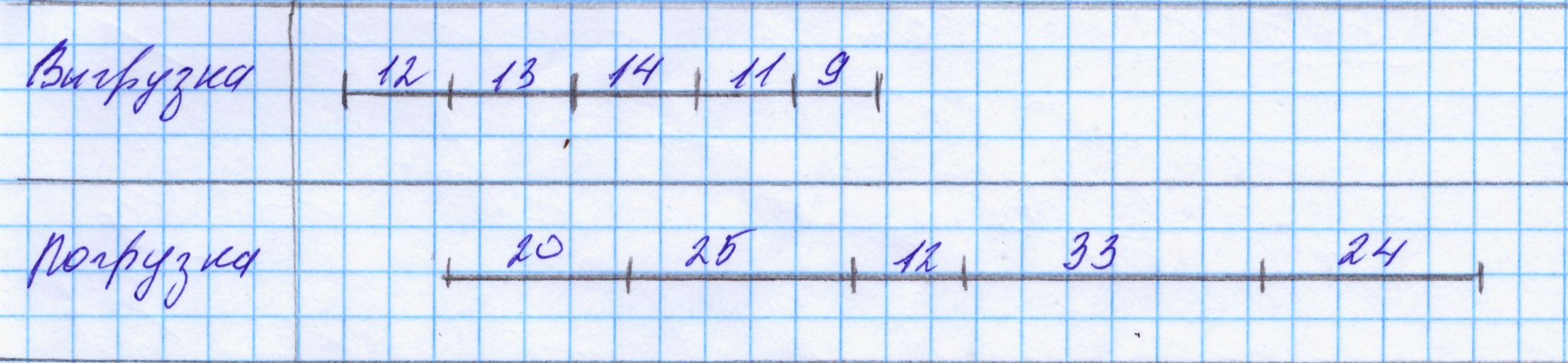


Рис. 1. График заданной очередности обработки судов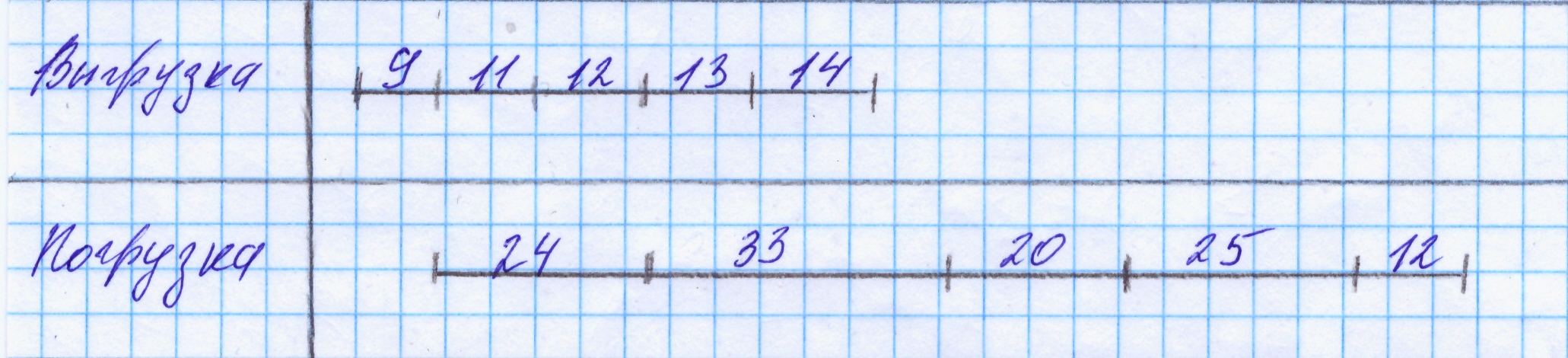


Рис. 2. График оптимальной очередности обработки судов
Далее определяем суммарное время обслуживания всех судов t_обр для обоих случаев очередности и разность между ними.

Σ t^з_обр=12+20+25+12+33+24=126 ч.

Σ t^о_обр=9+24+33+210+25+12=123 ч.

Σ t^з_обр- Σ t^о_обр=126-123=3ч.

Вывод: На графиках видно, что суммарное время выгрузки и погрузки всех судов сокращается на 3 часа, при оптимальной очередности.

Практическая работа № 2
Сетевые методы планирования и управления, используемые в операционной деятельности

Постановка задачи

Сетевые методы планирования и управления (СПУ) находят широкое использование при планировании и управлении сложными экономическими и техническими системами. Примерами объектов для применения этих методов могут быть проектирование и освоение производства новых изделий, составление планов развития и реконструкции предприятий, строительство крупных объектов, осуществление научных исследований и т. д.

СПУ широко применяются за рубежом и в России в самых различных сферах научной и промышленной деятельности, а именно: при создании новых типов судов, проектировании и постройке зданий, мостов, заводов, при разработке генеральных схем развития морских и речных портов. В указанных случаях необходимо:

1. Выполнить большое количество работ (операций).

2. Скоординировать в динамике совместную работу различных подразделений и организаций (исполнителей).

3. Обратить внимание на работы, влияющие на сроки выполнения всего намеченного комплекса работ.

4. Своевременно скорректировать принимаемые решения в ходе реализации на основе поступающей информации.

Применяемые для этого методы СПУ позволяют использовать для сбора и переработки информации ЭВМ, что способствует действенному руководству, осуществляемому в процессе проведения работ.

Владение методами СПУ необходимо для решения задач оптимизации распределения и взаимосвязи работ на стадии их оперативного регулирования с учетом реально действующих случайных воздействий различных факторов на ход работ. Таким образом, метод СПУ является важнейшим элементом стратегического управления.

Существуют различные графоаналитические методы разработки и внедрения целевых программ. Среди них весьма эффективным является американский метод СПУ (в американских названиях это системы PERT, SKANS и др.), или метод критического пути.

Основными понятиями данного метода являются:

– работа, т. е. какая-либо операция, имеющая продолжительность;

– фиктивная работа, не имеющая продолжительности, но введенная в схему для обозначения порядка следования реальных работ;

– событие (начало или завершение работы);

– критический путь (последовательность непосредственно следуемых друг за другом работ, образующих наибольшую продолжительность выполнения проекта).

Эффективность системы СПУ как инструмента стратегического управления долгосрочными программами инновационной деятельности состоит в том, что СПУ позволяет осуществить:

– прогнозирование сроков выполнения сложных инновационных проектов.

– сокращение продолжительности выполнения проектов средней и большой сложности на 15–20 %.

– снижение стоимости выполнения научно-исследовательских разработок на 10–15 %.

Задача практической работы состоит в следующем:

1) составление сетевого графика работ;

2) проведение его анализа;

3) поиск критического пути и расчет следующих показателей:

– раннего и позднего времени наступления событий;

– ранних и поздних сроков начала и окончания работ;

– полного и свободного резерва каждой работы;

– критического времени.

Исходные данные

Перечень работ — (i, j).

Продолжительность выполнения работ — t_ij.

Эти данные приведены в таблице 1.

Таблица 1

Работа (i,j)	Длительность работы, tij
(1,2)	5
(1,3)	12
(1,4)	6
(2,3)	5
(2,6)	14
(2,5)	9
(3,6)	10
(4,3)	11
(4,6)	7
(6,5)	13
(6,7)	6
(6,8)	13
(5,9)	10
(7,8)	7
(7,9)	5
(8,9)	4

Решение задачи
1. Построить сетевой график и ввести упорядоченную нумерацию событий и работ.

Построить сетевой график — значит, изобразить графически заданную последовательность выполнения работ. При этом работы изображаются стрелками, под которыми проставляется длительность выполнения работ tij. События изображаются кружочками, разделенными на сектора (рис. 1), в которых указываются следующие данные:

– номер события i;

– ранний срок наступления события — Tiр (наиболее ранний срок начала работ, следующих за событием i);

– поздний срок свершения события — Tiп (наиболее поздний срок окончания работ, предшествующих событию i).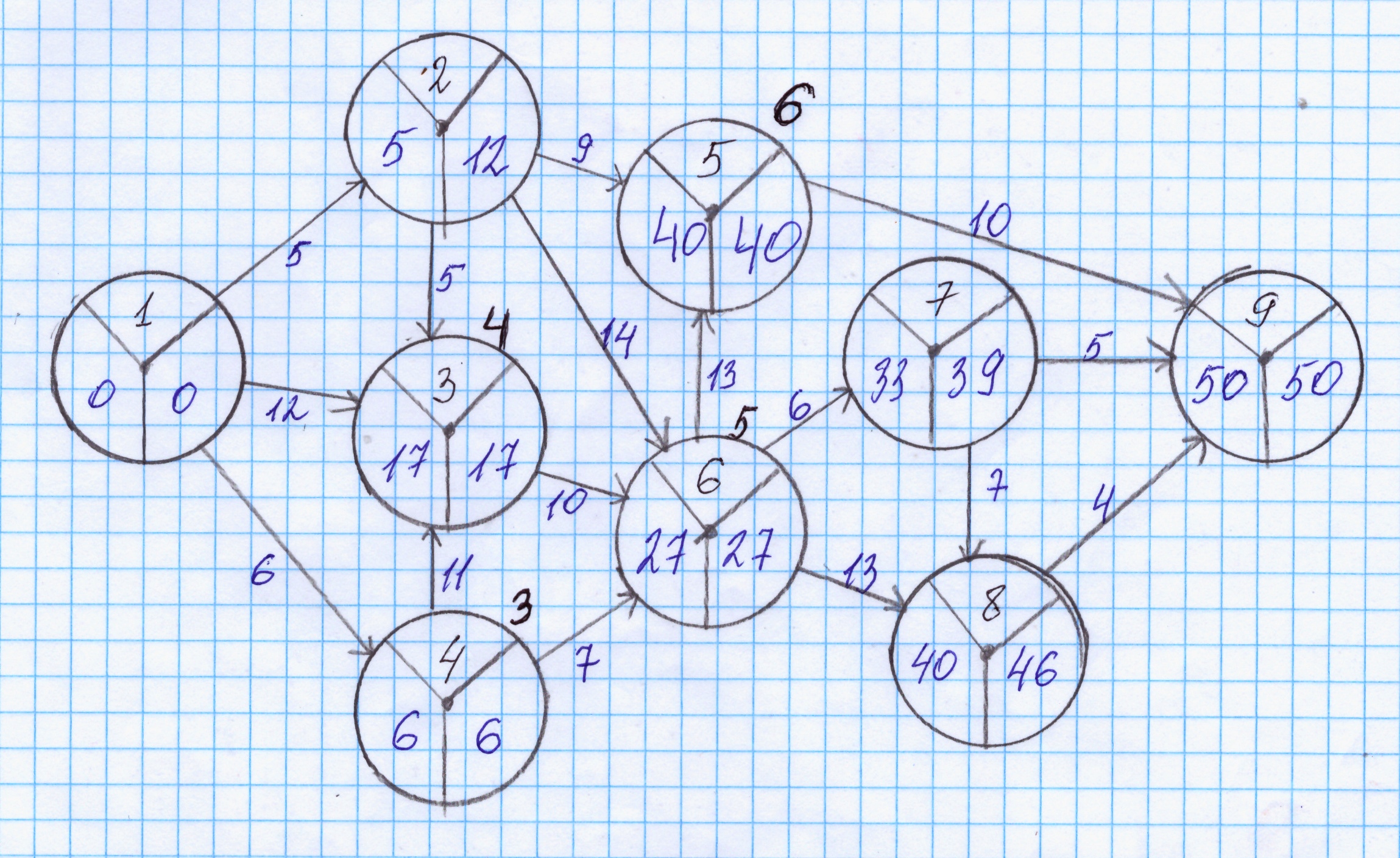



Рис. 1. Представление работ, событий и их характеристик на сетевом графике
2. Необходимо ввести упорядоченную нумерацию событий и работ, которую целесообразно выполнять согласно следующим условиям:

– событию может быть присвоен очередной номер, если пронумерованы все предшествующие ему работы;

– работе может быть присвоен очередной номер, если пронумеровано событие, после которого можно приступить к ее выполнению.

3. Определить параметры сетевого графика.

Рассчитываются характеристики событий и работ сетевого графика. При этом характеристики событий T_i(j)^р, T_i(j)^п вписываются в изображения событий сетевого графика, показанные кругами. Все характеристики работ t_ij записываются в таблицу (таблица 2).

Определить ранний срок Tjр наступления события j по формуле

T_j^р = max {T_i^р + t_ij}, i ϵ Ω_i,

где Ω_i - множество событий i, непосредственно предшествующих событию j;

t_ij — продолжительность выполнения работы (i, j).

Примеры расчета

T₆^р=max{T₃^р+t_3,6; T₄^р+t_4,6 T₅^р+t_2,6}=max{6+7;17+10;5+14}=max{13;27;19}=27.
Определить ранний срок начала работы (i, j):

t_ij^РН = T_i^р

Определить ранний срок окончания работы (i, j):

t_ij^РО = T_i^р + t_ij

Рассчитать критическое время по формуле T_кр = T_k^р,

где k — номер последнего события сетевого графика.

Определить поздний срок наступления события по формуле T_k^п = T_k^р = T_кр.

Определить поздний срок наступления события:

T_i^п = min {T_j^п – t_ij}, j ϵ Ω_j+,

где Ω_j+ - множество событий j, непосредственно следующих за событием i.
Примеры расчета

T_кр = T_k^р = 50

T_3,4^РН = 6

T_3,4^РО = T₃^р + t_3,4 = 6+11=17

T₂^п=min{T₅^п–t_2,5; T₆^п–t_2,6; T₃^п–t_2,3}=min{40-9; 27-14; 17-5}=min{31, 13, 12}=12
Поздний срок t_ij^ПО начала работы (i, j) определить по формуле

t_ij^ПО = T_j^п

Поздний срок t_ij^ПН начала работы (i, j) определить по формуле

t_ij^ПН = T_j^п – t_ij

Полный резерв времени выполнения работы и соотношения (1)–(6) — рассчитывается по формулам:

R_ij^п = t_ij^ПН - t_ij^РН = t_ij^ПО - t_ij^РО

R_ij^п = T_j^п – (T_i^р + t_ij)

Свободный резерв времени выполнения работы определяется по формуле

R_ij^с = T_j^п – t_ij^РО = T_j^р – (T_i^р + t_ij)
Примеры расчета

R_3,4^п = 6-6 = 0

R_3,4^п = 17-17 = 0

R_3,4^п = T₄^п – (T₃^р + t_3,4) = 17 - (6+11) = 0
R_5,6^п = 27 - 27 = 0

R_5,6^п = 40 - 40 = 0

R_5,6^п = T₆^п – (T5^р + t_5,6) = 40 - (27+10) = 0
R_3,4^с = T₄^п – t_3,4^РО = 17 – 17 = 0

R_3,4^с = T₄^р – (T₃^р + t_3,4) = 17 – (6 + 11) = 0
R_5,6^с = T₆^п – t_5,6^РО = 27 – 27 = 0

R_5,6^с = T₆^р – (T₅^р + t_5,6) = 40 – (27 + 13) = 0


4. Результаты расчетов должны быть представлены на сетевом гра- фике (см. пп. 1) и в следующей таблице:

Результаты анализа сетевого графика (характеристики работ)
Таблица 2

Работа в неупорядоченной нумерации	Работа в упорядоченной нумерации	Раннее начало tijРН	Позднее начало tijПН	Раннее окончание tijРО	Позднее окончание tijПО	Полный резерв работы Rijп	Свободный резерв работы Rijс
(1,2)	(1,2)	0	7	5	12	7	0
(1,3)	(1,4)	0	5	12	17	5	5
(1,4)	(1,3)	0	0	6	6	0	0
(2,3)	(2,4)	5	12	10	17	7	7
(2,6)	(2,5)	5	13	19	27	8	8
(2,5)	(2,6)	5	31	14	40	26	26
(3,6)	(4,5)	17	17	27	27	0	0
(4,3)	(3,4)	6	6	17	17	0	0
(4,6)	(3,5)	6	20	13	27	14	14
(6,5)	(5,6)	27	27	40	40	0	0
(6,7)	(5,7)	27	33	33	39	6	0
(6,8)	(5,8)	27	27	40	40	0	0
(5,9)	(6,9)	40	40	50	50	0	0
(7,8)	(7,8)	33	33	40	40	0	0
(7,9)	(7,9)	33	45	38	50	12	12
(8,9)	(8,9)	40	46	44	50	6	6