Практика физика. Федеральное агентство по образованию гоу впо тульский государственный университет Кафедра физики
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
|
8. Кинетическая энергия. Мощность. Работа. Кинетическая энергия катящегося тела 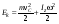 , где , где 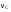 – скорость центра масс тела, – скорость центра масс тела, 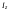 – момент инерции тела относительно оси вращения, проходящей через центр масс, – момент инерции тела относительно оси вращения, проходящей через центр масс,  – угловая скорость вращения. – угловая скорость вращения.Мощность 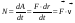 , где , где 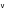 – скорость перемещения точки приложения силы. – скорость перемещения точки приложения силы.Работа силы 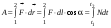 ,где ,где  – перемещение, – угол между вектором силы и вектором перемещения, – перемещение, – угол между вектором силы и вектором перемещения, 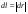 . .Работа момента силы 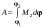 . .8-1. Шарик массы mи радиуса R катится по горизонтальной поверхности со скоростью  без проскальзывания. Найдите кинетическую энергию этого шарика. m = 1 кг, R= 1 м, без проскальзывания. Найдите кинетическую энергию этого шарика. m = 1 кг, R= 1 м, 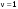 м/с. м/с.Ответ: 0,7 Дж 8-2. Диск массы mи радиуса R катится по горизонтальной поверхности со скоростью  без проскальзывания. Найдите кинетическую энергию этого диска. m = 1 кг, R= 1 м, без проскальзывания. Найдите кинетическую энергию этого диска. m = 1 кг, R= 1 м, 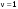 м/с. м/с.Ответ: 0,75 Дж  8-3. Катушка без ниток имеющая массу m, внешний радиус R и момент инерции I,катится по горизонтальной поверхности со скоростью 8-3. Катушка без ниток имеющая массу m, внешний радиус R и момент инерции I,катится по горизонтальной поверхности со скоростью  без проскальзывания. Найдите кинетическую энергию этой катушки. m = 1 кг, R= 1 м, I= 1 без проскальзывания. Найдите кинетическую энергию этой катушки. m = 1 кг, R= 1 м, I= 1 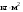 , , 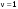 м/с. м/с.Ответ: 1 Дж 8-4. Небольшое тело начало движение из начала координат вдоль горизонтальной оси х под действием силы, направленной под углом = 30 к оси х. Модуль силы меняется в зависимости от координаты х по закону а) 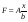 ; б) ; б) 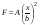 ; в) ; в) 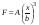 ; г) ; г) 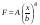 ; д) ; д) 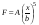 . Найти работу этой силы на участке пути от . Найти работу этой силы на участке пути от 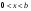 . А = 1 Н, b = 1 м. . А = 1 Н, b = 1 м.Ответы: а) 0,433 Дж; б) 0,289 Дж; в) 0,217 Дж; г) 0,173 Дж; д) 0,144 Дж 8-5. Небольшое тело начало движение из начала координат вдоль горизонтальной оси х под действием силы, направленной под углом к оси х. Модуль силы Fне меняется, но угол зависит от координаты х по закону 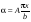 . Найти работу этой силы на участке пути от . Найти работу этой силы на участке пути от 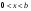 , если b = 1 м, F = 1 Н, а) А = 1 Н; б) А = , если b = 1 м, F = 1 Н, а) А = 1 Н; б) А = 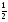 Н; в) А = Н; в) А = 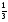 Н; г) А = Н; г) А = 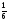 Н; д) А = Н; д) А = 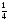 Н, Н, Ответы: а) 0 Дж; б) 0,637 Дж; в) 0,827 Дж; г) 0,955 Дж; д) 0,9 Дж 8-6. Найти работу, произведенную машиной за промежуток времени  с, если мощность машины зависит от времени по закону с, если мощность машины зависит от времени по закону а) 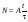 ; б) ; б) 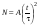 ; в) ; в) 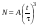 ; г) ; г) 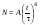 ; д) ; д) 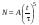 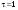 с, А = 1 Вт. с, А = 1 Вт.Ответы: а) 0,5 Дж; б) 0,333 Дж; в) 0,25 Дж; г) 0,2 Дж; д) 0,167 Дж 8-7. Массивный диск может вращаться вокруг закрепленной оси без трения. Найдите работу момента силы при повороте диска на угол 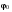 , если момент сил, действующий на диск, зависит от угла поворота , если момент сил, действующий на диск, зависит от угла поворота 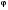 по закону по закону а) 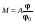 ; б) ; б) 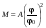 ; в) ; в) 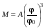 ; г) ; г) 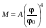 ; ; А = 1 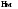 , , 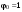 рад. рад.Ответы: а) 0,5 Дж; б) 0,333 Дж; в) 0,25 Дж; г) 0,2 Дж  8-8. Тело движется вдоль горизонтальной оси х под действием силы 8-8. Тело движется вдоль горизонтальной оси х под действием силы 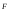 , направленной под углом к оси х. В некоторый момент тело достигает скорости , направленной под углом к оси х. В некоторый момент тело достигает скорости 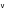 . Найдите мощность силы в этот момент времени. F = 1 Н, . Найдите мощность силы в этот момент времени. F = 1 Н, 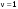 м/с, = 30. Ответ: 0,866 Вт м/с, = 30. Ответ: 0,866 Вт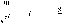 8-9. Тонкий однородный стержень массы m и длины l может вращаться вокруг горизонтальной оси, проходящей через конец стержня. Стержень привели в горизонтальное положение и толкнули так, что незакрепленный конец стержня приобрел скорость 8-9. Тонкий однородный стержень массы m и длины l может вращаться вокруг горизонтальной оси, проходящей через конец стержня. Стержень привели в горизонтальное положение и толкнули так, что незакрепленный конец стержня приобрел скорость  . Найдите кинетическую энергию стержня в первый момент времени. m=1 кг, l= 1 м, . Найдите кинетическую энергию стержня в первый момент времени. m=1 кг, l= 1 м, 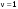 м/с. Ответ: 0,167 Дж м/с. Ответ: 0,167 Дж8-10. Шарик массы mи радиуса R катится без проскальзывания по горизонтальной поверхности, вращаясь с угловой скоростью . Найдите кинетическую энергию этого шарика. m = 1 кг, R= 1 м, = 1 рад/с. Ответ: 0,7 Дж 8-11. Диск массы mи радиуса R катится без проскальзывания по горизонтальной поверхности, вращаясь с угловой скоростью . Найдите кинетическую энергию этого диска. m = 1 кг, R= 1 м, = 1 рад/с. Ответ: 0,75 Дж 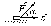 8-12. Тело движется вдоль горизонтальной оси х под действием силы 8-12. Тело движется вдоль горизонтальной оси х под действием силы 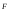 , направленной под углом к оси х. В некоторый момент тело достигает скорости , направленной под углом к оси х. В некоторый момент тело достигает скорости 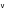 , а мощность силы равна N. Найдите а) косинус угола ; б) синус угола . , а мощность силы равна N. Найдите а) косинус угола ; б) синус угола .F = 1 Н, 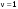 м/с, N= 0,5 Вт. Ответы: а) 0,5; б) 0,866 м/с, N= 0,5 Вт. Ответы: а) 0,5; б) 0,866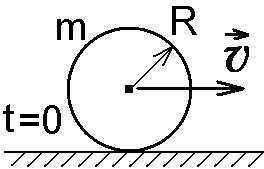 8-13э. В начальный момент времени t = 0 тонкий обруч с массой m = 0,1 кг и с радиусом R = 0,5 м не вращался, а поступательно скользил по горизонтальной поверхности с кинетической энергией 800 Дж. Под действием силы трения он начал катиться без проскальзывания с кинетической энергией поступательного движения 200 Дж. Сила трения совершила работу: а) 300 Дж б) 600 Дж в) 500 Дж г) 400 Дж  8-14э. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости , при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 2r1 и раскрутили до той же угловой скорости. Какая работа при этом была совершена? 8-14э. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости , при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 2r1 и раскрутили до той же угловой скорости. Какая работа при этом была совершена?1) А2 = 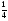 А1 2) А2 = 2А1 3) А2 = А1 2) А2 = 2А1 3) А2 = 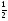 А1 4) А2 = 4А1 А1 4) А2 = 4А19. Закон сохранения импульса и момента импульса. При взаимодействии частиц системы между собой полный вектор импульса системы остается постоянным в случаях, когда а) 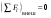 , б) , б) 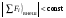 и время взаимодействия очень мало. В этих случаях и время взаимодействия очень мало. В этих случаях 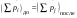 , где , где 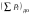 – векторная сумма импульсов частиц, которые существовали до взаимодействия, – векторная сумма импульсов частиц, которые существовали до взаимодействия, 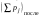 – векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если – векторная сумма импульсов всех частиц, которые будут существовать после взаимодействия. Если 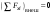 , то сохраняется только проекция полного импульса системы на ось x, , то сохраняется только проекция полного импульса системы на ось x, 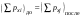 . .При взаимодействии частиц системы между собой полный вектормомента импульса системы остается постоянным в случаях, когда а) 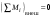 , б) , б) 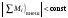 и время взаимодействия очень мало. В этих случаях и время взаимодействия очень мало. В этих случаях 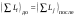 где где 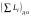 – векторная сумма моментов импульсов частиц, которые существовали до взаимодействия, – векторная сумма моментов импульсов частиц, которые существовали до взаимодействия, 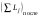 – векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если – векторная сумма моментов импульсов всех частиц, которые будут существовать после взаимодействия. Если 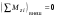 , то сохраняется только проекция момента импульса системы на ось z , то сохраняется только проекция момента импульса системы на ось z 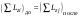 (часто относительно закрепленной оси вращения). (часто относительно закрепленной оси вращения).Момент импульса частицы 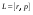 , где , где 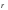 – радиус-вектор частицы, – радиус-вектор частицы, 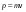 – импульс частицы. – импульс частицы. 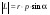 , где – угол между , где – угол между 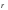 и и 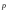 . Для твердого тела, вращающегося вокруг закрепленной оси z . Для твердого тела, вращающегося вокруг закрепленной оси z 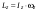 , где , где 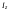 – момент инерции тела относительно оси z, – момент инерции тела относительно оси z, 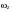 – угловая скорость. – угловая скорость. 9-1. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 9-1. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 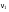 . Под углом к направлению его движения летит второй шарик массы m2 со скоростью . Под углом к направлению его движения летит второй шарик массы m2 со скоростью 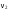 и сталкивается с первым. Шарики слипаются и движутся под углом к первоначальному направлению движения и сталкивается с первым. Шарики слипаются и движутся под углом к первоначальному направлению движения А) первого шарика; Б) второго шарика. Найдите 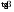 . . 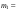 1 кг, 1 кг,  2 кг, 2 кг, 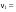 1 м/с, 1 м/с, 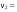 2 м/с, 2 м/с, а) = 30; б) = 45; в) = 60; г) 90. А) Ответы: а) 0,448; б) 0,739; в) 1,155; г) 4 Б) Ответы: а) 0,103; б) 0,15; в) 0,192; г) 0,25  9-2. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 9-2. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 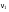 . Под углом к направлению его движения летит второй шарик массы m2 со скоростью . Под углом к направлению его движения летит второй шарик массы m2 со скоростью 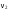 и сталкивается с первым. Шарики слипаются и движутся под со скоростью и сталкивается с первым. Шарики слипаются и движутся под со скоростью 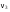 . Найдите после удара . Найдите после удара А) модуль скорости 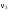 ; Б) модуль импульса шариков. ; Б) модуль импульса шариков.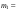 1 кг, 1 кг,  2 кг, 2 кг, 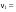 1 м/с, 1 м/с, 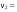 2 м/с, а) = 30, б) = 45, в) = 60. 2 м/с, а) = 30, б) = 45, в) = 60.А) Ответы: а) 1,63 м/с; б) 1,59 м/с; в) 1,53 м/с Б) Ответы: а) 4,89 кгм/с; б) 4,76 кгм/с; в) 4,58 кгм/с 9-3. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 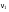 . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью 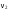 и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара и сталкивается с первым. Шарики слипаются и далее движутся вместе. Найдите после удара а) модуль импульса шариков; б) модуль скорости шариков. 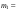 1 кг, 1 кг,  2 кг, 2 кг, 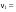 1 м/с, 1 м/с, 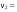 2 м/с. 2 м/с.Ответ: а) 4,123 кгм/с; б) 1,374 м/с 9-4. Маленький пластилиновый шарик массы m1 движется горизонтально со скоростью 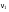 . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью . Перпендикулярно к направлению его движения летит второй шарик массы m2 со скоростью 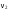 и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом к первоначальному направлению движения А) первого шарика; Б) второго шарика. Найдите и сталкивается с первым. Шарики слипаются и далее движутся вместе под углом к первоначальному направлению движения А) первого шарика; Б) второго шарика. Найдите 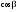 и и 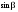 . .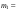 1 кг, 1 кг,  2 кг, 2 кг, 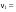 1 м/с, 1 м/с, 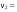 2 м/с. 2 м/с.А) Ответы: 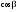 = 0,243; = 0,243; 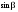 = 0,97 = 0,97Б) Ответы: 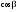 = 0,97; = 0,97; 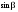 = 0,243 = 0,2439-5. На горизонтальной плоскости лежит тонкий однородный стержень массы m =1 кг и длины l, который может вращаться вокруг вертикальной оси, проходящей через А) центр масс стержня С; Б) конец стержня О. Под углом =30 к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью  = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения . Найти = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения . Найти а) угловую скорость вращения системы после удара, если l= 1 м; б) длину стержня, если , = 1 рад/с А)  Б) Б) 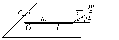 Ответы: Аа) 0,75 рад/с; Ба) : 0,375 рад/с; Аб) 0,75 м; Бб) 0,375 м 9-6. Тонкий однородный диск массы m = 1 кг и радиуса R может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей А) через его край О; Б) через его центр С. Под углом =30 а) к вертикали; б) к горизонтали в плоскости вращения диска движется маленький пластилиновый шарик такой же массы m со скоростью  = 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращения w.. Найти = 1 м/с. Шарик прилипает к нижней точке неподвижно висящего диска, и система приобретает угловую скорость вращения w.. Найти 1) угловую скорость вращения системы после удара, если R= 1 м; 2) Найти радиус диска, если = 1 рад/с, Аа) 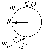 Ба) Ба) 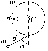 Аб) Аб)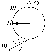 Бб) Бб)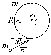 Ответы: 1) Аа) 0,182 рад/с; Ба) 0,333 рад/с; Аб) 0,315 рад/с; Бб) 0,577 рад/с. Ответы: 2) Аа) 0,182 м; Ба) 0,333 м; Аб) 0,315 м; Бб) 0,577 м.  9-7. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями 9-7. Тонкий однородный стержень массы m = 1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. С разных сторон на стержень горизонтально в той же плоскости налетают два одинаковых пластилиновых шарика той же массы m с одинаковыми скоростями  = 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость . Найти = 1 м/с. Первый шарик застревает в центре стержня, второй – в нижнем конце, и система приобретает угловую скорость . Найти а) угловую скорость вращения системы после удара, если l= 1 м; б) Найти длину стержня, если = 1 рад/с. Ответы: а) 0,316 рад/с; б) 0,316 м  9-8. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью 9-8. Тонкий однородный стержень массы m =1 кг и длины l может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает пластилиновый шарик той же массы m со скоростью  = 1 м/с. Шарик застревает в точке А стержня на расстоянии х= = 1 м/с. Шарик застревает в точке А стержня на расстоянии х= 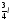 от точки О, и система приобретает угловую скорость . Найти от точки О, и система приобретает угловую скорость . Найти а) угловую скорость вращения системы после удара, если l= 1 м; б) Найти длину стержня, если = 1 рад/с. Ответы: а) 0,837 рад/с; б) 0,837 м. 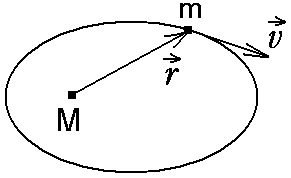 9-9э. Планета массой  движется по эллиптической орбите, в одном из фокусов которой находится звезда массы движется по эллиптической орбите, в одном из фокусов которой находится звезда массы  . .  радиус-вектор планеты (см.рисунок). Выберите правильное утверждение: радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:а) момент импульса планеты относительно центра звезды меняется и максимален при наибольшем ее удалении  от звезды от звездыб) момент силы тяготения, действующей на планету (относительно центра звезды), изменяется, но направлен перпендикулярно плоскости орбиты в) величина момента импульса планеты относительно центра звезды в любой момент времени определяется выражением  г) момент импульса планеты относительно центра звезды не изменяется  9-10э. Два невесомых стержня длины b соединены под углом 1 = 60 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью . На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до 2 = 120. С какой угловой скоростью стала вращаться такая система? 9-10э. Два невесомых стержня длины b соединены под углом 1 = 60 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью . На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до 2 = 120. С какой угловой скоростью стала вращаться такая система?1) 3 2)  3) 3) 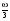 4) 4)  5) 5) |
