Федеральное государственное бюджетное образовательное учреждение высшего образования московский авиационный институт
 Скачать 0.92 Mb.
|
|
2.2.Расчет параметров сканирования и частот кругового обзора Минимальный угловой размер цели: 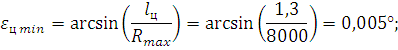 Для наилучшего обнаружения от цели необходимо принять, по крайней мере, от 5 до 10 импульсов. Отсюда находится время минимальное облучения цели  : Это минимальное время, за которое лепесток сканирования должен пройти по окружности диаграммы направленности, при этом захватывая цель. Схема расположения лепестков показана на рисунке 2. 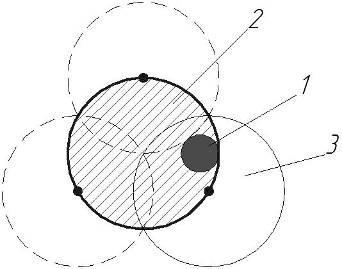 Рисунок 2.2 - Расположение лепестков сканирования и диаграммы направленности антенны: 1 – область цели; 2 – область диаграммы направленности; 3 – область лепестка сканирования. Из геометрических соотношений 3-х лепестковой системы сканирования, найдем максимальную частоту кругового вращения лепестка (передатчика):  Нижняя граница частоты кругового вращения лепестка зависит от разрешающей способности РЛС, которая, в свою очередь, зависит от максимальной скорости цели на максимальном расстоянии от системы. Разрешающая способность РЛС определяется по формуле: 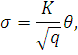  гдеK – коэффициент потерь мощности сигнала, 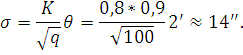 – коэффициент использования площади антенны (принимаем  , – коэффициент потерь в радиочастотах (принимаем  , – ширина диаграммы направленности, – динамический диапазон РЛС (принимаем q = 40 дБ). Для безошибочного определения положения цели, необходимо, чтобы линейное перемещение цели 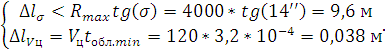 за время облучения не превышало линейную разрешающую способность  РЛС. где  - максимальная скорость движения цели. Условие 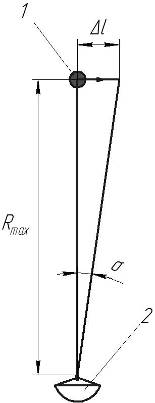> выполняется. Рисунок 2.3- Угловая разрешающая способность РЛС: 1 – цель, 2 – антенна Тогда требуемая частота сканирования находится в диапазоне:    Принимаем  .Длительность сканирования зависит также от углового размера сканируемой области и определяется по формуле:  где  - максимальный угол сканируемой области, Принимаем  = 10 с.Определение частоты поворота антенны. Частота вращения антенны определяется по формуле:  гдеN – число витков в траектории движения конца антенны. 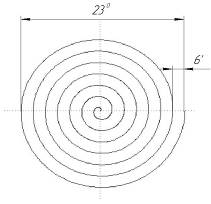 Рисунок 2.4- Траектория движения конца антенны.   Определим время, за которое совершается один виток:  Определение диаметра антенны:  Оценка требуемых параметров движения антенны в режиме поиска цели В режиме поиска цели за счет спирального сканирования угловые скорости и ускорения могут достигать существенных значений. Для оценки указанных скоростей и ускорений рассмотрим движение линии визирования антенны в режиме сканирования. Для сканирования по сворачивающейся спирали можно записать:   где  – максимальная амплитуда угла относительно центра.Если задан шаг спирали 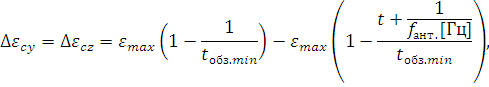, то частоту сканирования можно найти следующим образом: Преобразуя формулы, найдем: 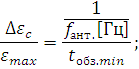  Это нереализуемое требование кК мощности исполнительного двигателя, поэтому примем  , тогда  Дифференцируя формулы угла, получим зависимости для угловых скоростей при сканировании:   Дифференцируя уравнения скорости, найдем угловые ускорения:   Определим максимальные значения угловых скоростей сканирования для принятых параметров:    Построим трехмерную модель параболической антенны с помощью ППП SolidWorks и узнаем ее массовые характеристики. Габариты антенны представлены на рис. 7: 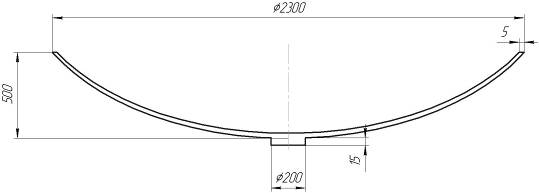 Рисунок 2.5- Параболическая антенна в разрезе. Масса антенны m=38 кг, момент инерции нагрузки антенны IН=3,85 кг∙м2, материал – алюминиевый сплав. Расчет передаточного числа редуктора. 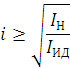  - передаточное число редуктора;где 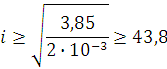 - момент инерции нагрузки антенны; - момент инерции исполнительного двигателя. Примем  Расчет момента на валу.   - максимальный момент нагрузки, приведенный к валу исполнительного двигателя; - максимальное угловое ускорение нагрузки (в установившемся режиме). радиолокационный станция частота сигнал Следовательно:  Расчет требуемой максимальной угловой скорости двигателя:   – максимальная угловая скорость двигателя; - максимальная угловая скорость нагрузки; - передаточное число редуктора. Расчет мощности на валу, требуемой для воспроизведения заданного движения нагрузки.  В соответствии с полученными данными выберем двигатель марки МД 220-60. Его характеристики приведены в таблице 2.1. Таблица 2.1.
Структурная схема замкнутого контура следящего привода показана на рис. 2.6. 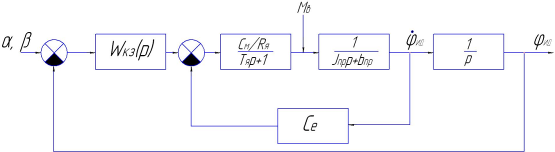 Рисунок 2.6- Структурная схема замкнутого контура следящего привода См – коэффициент момента, Се – коэффициент противо-ЭДС, Rя – сопротивление фазы, Тя – электромагнитная постоянная, Jпр – приведенный к валу двигателя момент инерции, bпр – коэффициент демпфирования. Момент инерции, приведенный к валу двигателя, определяется по формуле:  Коэффициент демпфирования определяется по формуле:  Частота среза системы равна: 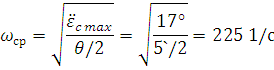 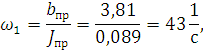 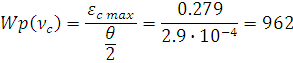  Постоянные времени: 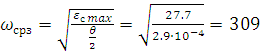 частота среза запретной зоны системы; M=1,1…1,3 – показатель колебательности; 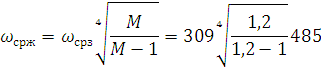 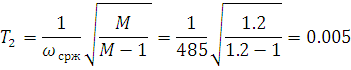 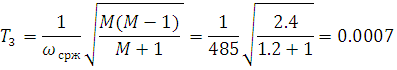 На основании полученных данных построим желаемую частотную характеристику системы (рис. 2.7). 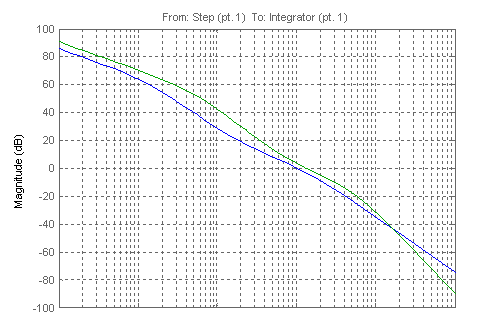 Рисунок 2.7- Частотные характеристики системы: 1-желаемая, 2-располагаемая. Схема моделирования разомкнутой системы следящего привода представлена на рис. 2.8. 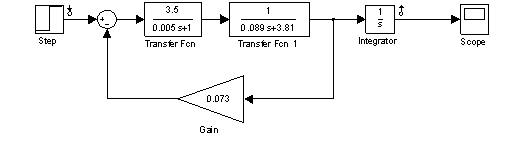 Рисунок 2.8. -Схема моделирования разомкнутой системы следящего привода. ЛАФЧХ разомкнутой системы представлена на рис. 2.9: 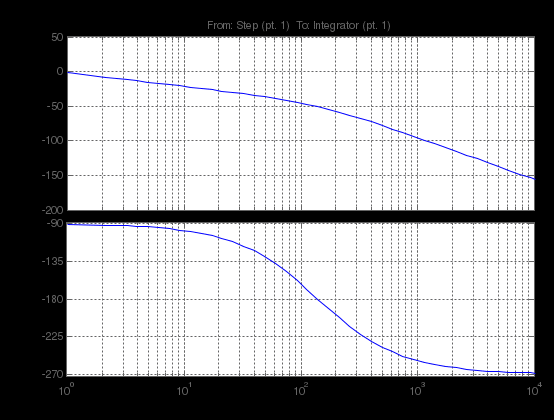 Рисунок 2.9- ЛАФЧХ разомкнутой системы Как видно из графика, амплитуда не удовлетворяет требованиям желаемой характеристики, поскольку располагается ниже необходимого уровня. Чтобы повысить амплитуду, введем в схему следящего привода корректирующее звено. Схема моделирования разомкнутой системы с корректирующим звеном показана на рис. 2.10: 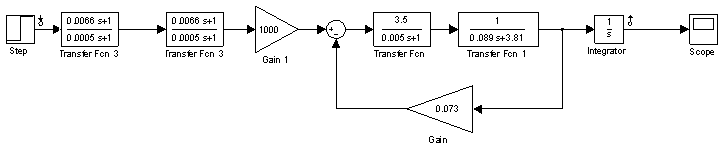 Рисунок 2.10- Схема моделирования разомкнутой системы с корректирующим звеном ЛАФЧХ разомкнутой системы представлена на рис. 2.11. 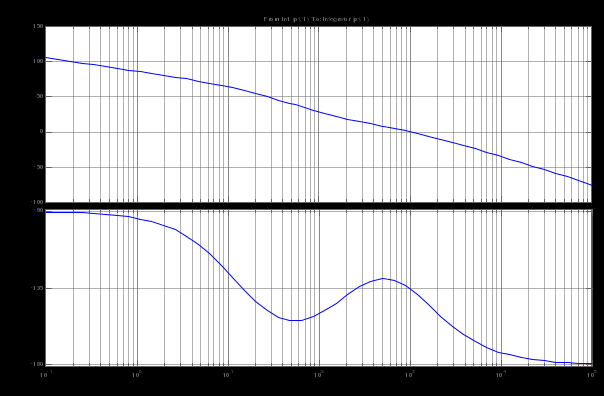 Рисунок 2.11-ЛАФЧХ разомкнутой системы Благодаря введению корректирующего звена удалось повысить коэффициент усиления системы так, что характеристика располагается выше желаемой и, следовательно, удовлетворяет требованию работоспособности привода. Схема моделирования замкнутой системы представлена на рис. 2.12: 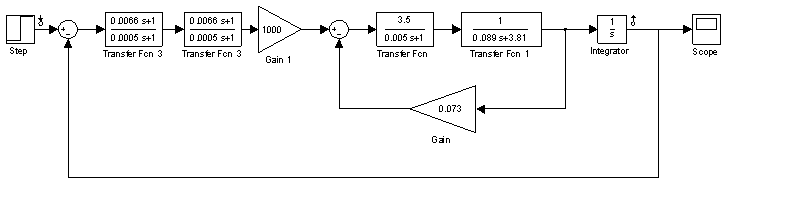 Рисунок 2.12- Схема моделирования замкнутой системы Переходный процесс замкнутой системы представлены на рис. 2.13: 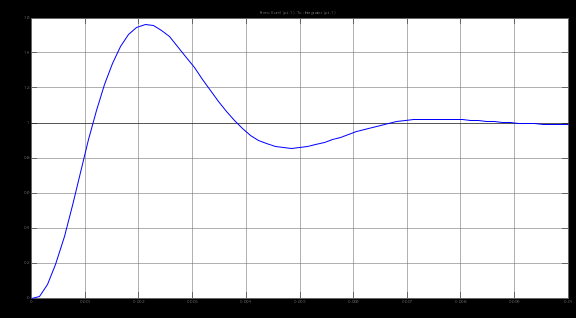 Рисунок 2.13- Переходный процесс замкнутой системы Из графика видно, что переходный процесс имеет большую колебательность, величина перерегулирования определяется по формуле: 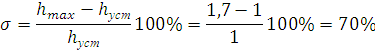  - перегулирование – максимальное отклонение от установившегося значения, выраженное в относительных единицах или процентах,hmax – максимальное отклонение от установившегося значения, hуст – установившееся значение. ЛАФЧХ замкнутой системы представлена на рис. 2.14: 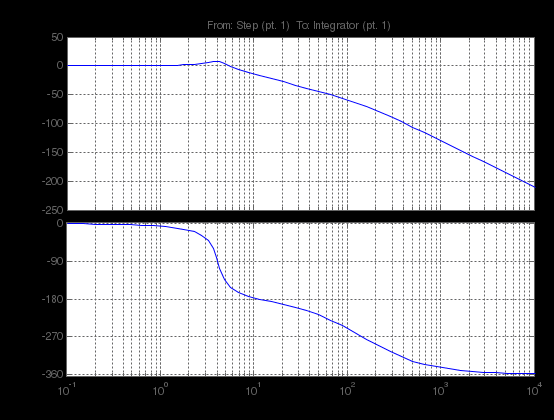 Рисунок 2.14- ЛАФЧХ замкнутой системы Запас по амплитуде равен -20 дБ, запас по фазе составляет 40°. Статическая ошибка равна 3.24 дБ. На рисунке 2.15 показан переходный процесс по ошибке. 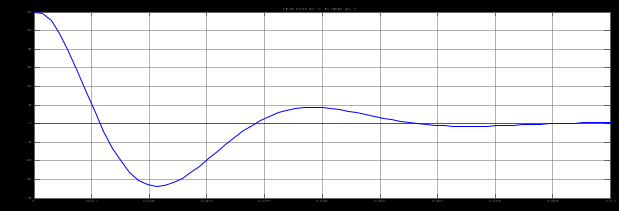 Рисунок 2.15 – Переходный процесс по ошибке Из графика видно, что точность разработанной системы соответствует техническому заданию. |
, Ом, ±15% 
, 
, рад/с 
,, мс
, мс
,, В/рад/с
,, 