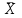статистика двагс вар 20. Задача 1 Описательная статистика. 3
 Скачать 270.94 Kb. Скачать 270.94 Kb.
|
|
Содержание Задача №1 Описательная статистика. 3 Задача №2. Корреляционно–регрессионный анализ 11 Задача №3. Анализ временных рядов и прогнозирование. 15 Абсолютные и относительные показатели тенденции 17 Задача № 4. Индексы и их применение в экономических исследованиях. 23 Список использованной литературы 27 Задача №1 Описательная статистика. В банке в течение дня были зафиксированы следующие суммы закладных на 20 домов
Построить дискретный ряд распределения частот, относительных частот и накопленных частот. Построить полигон частот (или относительных частот) и эмпирическую функцию распределения. Найдите среднюю арифметическую, моду, медиану, первый и третий квартиль, межквартильный размах, стандартное отклонение, коэффициенты асимметрии и эксцесс. Проанализировать результаты, используя эти характеристики. Вычислить доверительный интервал для средней генеральной. Построить интервальный ряд распределения частот, относительных частот и накопленных частот, предварительно определив оптимальное число интервалов. Построить полигон частот (или относительных частот) и гистограмму частот (или относительных частот). Найти среднюю арифметическую, моду, медиану, первый и третий квартиль, межквартильный размах, коэффициент вариации, исправленную выборочную дисперсию, коэффициенты асимметрии и эксцесса. Найти доверительный интервал для средней арифметической генеральной совокупности при уровне значимости α=0,05. На основании полученных результатов сделать вывод о виде распределения генеральной совокупности и указать интервал, включающий 50% центральных значений указанных величин. Решение. 1. Построить дискретный ряд распределения частот, относительных частот и накопленных частот. Отсортируем заданный ряд по возрастанию Таблица 2 Отсортированные данные о стоимости закладных
Построим дискретный ряд распределения частот Таблица 3 Дискретный ряд распределения частот
Относительная частота получается делением частот на объем выборки. Если просуммировать частоты данной группы с частотами последующих групп, то получим накопленные частоты. 2. Построим полигон частот (рис. 1) и эмпирическую функцию распределения (рис. 2). 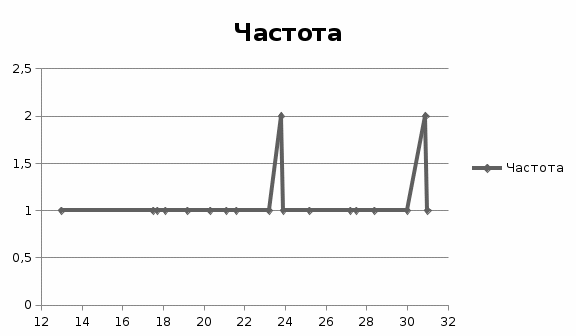 Рисунок 1. Полигон частот Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события {X 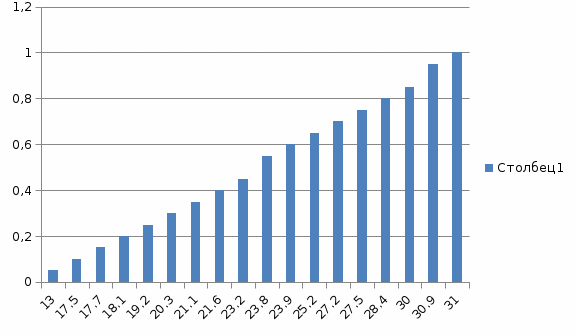 Рисунок 2. Эмпирическая функция распределения 3. Найдем среднюю арифметическую, моду, медиану, первый и третий квартиль, межквартильный размах, стандартное отклонение, коэффициенты асимметрии и эксцесс. Проанализируем результаты, используя эти характеристики. Построим вариационный ряд, упорядочив данные по возрастанию. 13 17,5 17,7 18,1 19,2 20,3 21,1 21,6 23,2 23,8 23,8 23,9 25,2 27,2 27,5 28,4 30 30,9 30,9 31 Средняя арифметическая величина стоимости закладных определяется по формуле хср = (хi) / n, т.е. сумма набора вариант делится на их число. хср = 474,3 / 20 = 23,7 Мода представляет собой значения, встречающиеся в ряде распределения с наибольшей частотой. Величины 25,2 и 30,9 встречаются по два раза. Медиана равна средней варианте упорядоченного ряда. Так как количество данных четное, медиану находим как среднее арифметическое из х10 и х11: (23,8 + 23,8) / 2 = 23,8 Первый квартиль находим как среднее арифметическое из из х5 и х6: (19,2+ 20,3) / 2 = 19,75 Третий квартиль находим как среднее арифметическое из из х15 и х16: (27,5 + 28,4) / 2 = 27,95 Межквартильный размах равен 27,95 – 23,8 = 8,2. Для определения стандартного отклонения проведем в таблице следующие расчеты (таблица 2). Имеем: Среднее арифметическое отклонение MD = 83,47 / 19 = 4,39; Хср. = 474,3 / 20 = 23,715; S2 = 511,27 / 19 = 25,56; Стандартное отклонение или среднее квадратическое отклонение S = 5,06 Асимметрия а3 = -444,87/(20х5,063) = -0,17<0 Имеется отрицательная асимметрия. Эксцесс а4 = 28141,45 / (20 х 5,064) = 2,15<3 – эксцесс меньше нормального. Таблица 2 Данные для определения стандартного отклонения, асимметрии и эксцесса
Основные показатели формы распределения – асимметрия и эксцесс – характеризуют степень отклонения реального рассматриваемого ряда распределения от нормального распределения. Согласно проведенному анализу асимметрии и эксцесса, выдвигаем гипотезу о нормальном распределении генеральной совокупности. 4 Вычислим доверительный интервал для средней генеральной Имеем хср = 23,715 Среднее квадратическое отклонение S = 5,06 При n = 20 имеем ν=20-1 = 19 При α=0,05 t0.025=2.093 Тогда доверительный интервал для средней определится из  или 23,72±2,093 х 5,06 = 23,72±10,58. Окончательно имеем (13,13; 34,30). или 23,72±2,093 х 5,06 = 23,72±10,58. Окончательно имеем (13,13; 34,30).Итак, в 95 случаях из 100 стоимость закладной составит от 13,13 до 34,30 руб. 5. Построить интервальный ряд распределения частот, относительных частот и накопленных частот, предварительно определив оптимальное число интервалов. Наилучшим числом интервалов группировки («формула Стерджесса») является k = 1+3.322lg(n) . Здесь lg(n) – десятичный логарифм количества данных. k = 1+3.222 x lg20 = 5 Разделим данные на 5 групп. Размер группы определяется размахом вариации (разность между наибольшим и наименьшим значением, деленным на число групп: 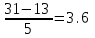 Взяв за нижний предел первой группы 52, получим следующие интервалы: 13 – 16,6, 16,6 – 20,2, 20,2 – 23,8, 23,8 – 27,4, 27,4 – 31. Подсчитав, сколько наблюдений попало в каждую группу, получим ряд распределения (таблица 5). Таблица 5 Ряд распределения
Относительные частоты получаются делением частот на объем выборки. В группу включаются и те измерения, которые в точности равны нижнему или верхнему пределу. 6. Построить полигон частот (или относительных частот) и гистограмму частот (или относительных частот). Графическое представление ряда распределения может быть получено с помощью гистограммы и полигона, которые приведены на рис. 3 и рис. 4. 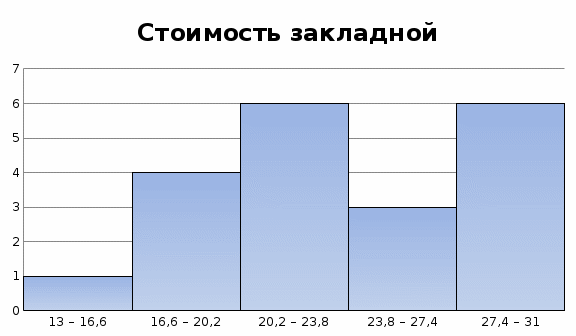 Рисунок 3. Гистограмма частот  Рисунок 4. Полигон частот По горизонтальной оси гистограммы отложены границы групп, а полигона – центры групп. По вертикальной оси в обоих случаях откладываются частоты групп, а полигона – центры групп. В случае полигона частоты откладываются на перпендикулярах, восстановленных из центров групп. 7. Найти среднюю арифметическую, моду, медиану, первый и третий квартиль, межквартильный размах, коэффициент вариации, исправленную выборочную дисперсию, коэффициенты асимметрии и эксцесса. Формула для расчета средних величин: xср = (хi*fi) / (fi), где n – численность совокупности; хi – варианта или значение признака (для интервального ряда принимает серединное значение x’i); fi – частота повторения индивидуального значения признака (его вес). 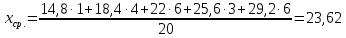 Медиана равна средней варианте упорядоченного ряда, т.е. Ме = 22 В то время, как медиана делит распределение на две половины, квартили делят его на четыре равные части. Мода представляет собой значения, встречающиеся в ряде распределения с наибольшей частотой. Первый квартиль равен 18,4, третий квартиль – 25,6. Межквартильный размах равен 25,6 – 18,4 = 7,2. Полуразмах квартилей составляет 7,2 / 2 = 3,6 Следовательно, примерно 50 % наблюдений заключено в пределах 23,62 ±3,6, т.е. от 20,02 до 27,22. Тот факт, что медиана меньше среднего значения, говорит о том, что ряд не симметричен относительно середины. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.
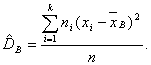 Dв=401,11/20 = 20,06 Для исправления выборочной дисперсии достаточно умножить ее на дробь S2 = 20,06 х 20 / 19 = 21,11 S = √21,11=4,59 Коэффициент вариации V = S / Хср. = 4,59/23,62 х 100 % = 19,45 % Поскольку V<33 %, результаты однородны. Асимметрия а3 = -214,85/(20х4,593) = -0,11<0 Имеется отрицательная асимметрия. Эксцесс а4 = 14925,84 / (20 х 4,594) = 1.7<3 – эксцесс меньше нормального. 8. Найти доверительный интервал для средней арифметической генеральной совокупности при уровне значимости α=0,05. Имеем хср = 23,62 Среднее квадратическое отклонение S = 4,59 При n = 20 имеем ν=20-1 = 19 При α=0,05 t0.025=2.093 Тогда доверительный интервал для средней определится из  или 23,62±2,093 х 4,59 = 23,62±9,62. Окончательно имеем (14,00; 33,24). или 23,62±2,093 х 4,59 = 23,62±9,62. Окончательно имеем (14,00; 33,24).Итак, в 95 случаях из 100 стоимость закладной составит от 14,00 до 33,24 руб. 9. На основании полученных результатов сделать вывод о виде распределения генеральной совокупности и указать интервал, включающий 50% центральных значений указанных величин. Согласно проведенному анализу асимметрии и эксцесса, выдвигаем гипотезу о нормальном распределении генеральной совокупности. Примерно 50 % наблюдений заключено в пределах 20,02 – 27,22. Задача №2. Корреляционно–регрессионный анализ Анализ дорожно-транспортных происшествий в 10 городах дал следующую статистику относительно процента водителей моложе 21 года и числа происшествий с тяжелыми последствиями на 1000 водителей (таблица 2.1). Таблица 2.1
Провести графический и корреляционный анализ полученных данных и сделать соответствующие выводы и рекомендации. Спрогнозируйте число ДТП с тяжелыми последствиями для города, в котором число водителей моложе 21 года равно 20% от общего числа водителей. Решение. 1. Построим корреляционное поле для двумерной выборки. Изучим представленные данные с использованием графического представления, изобразив каждую пару данных в виде точки в системе координат, по горизонтальной оси которой отложены значения независимой переменной (нашем случае – процент водителей моложе 21 года), по вертикальной – зависимую переменную – число происшествий с тяжелыми последствиями на 1000 водителей. Получим корреляционное поле для двумерной выборки (рис. 4). Как видим, несмотря на некоторый разброс данных, их можно приближенно описать линейной зависимостью, уравнение которой в общем виде может быть записано: у=а+bx  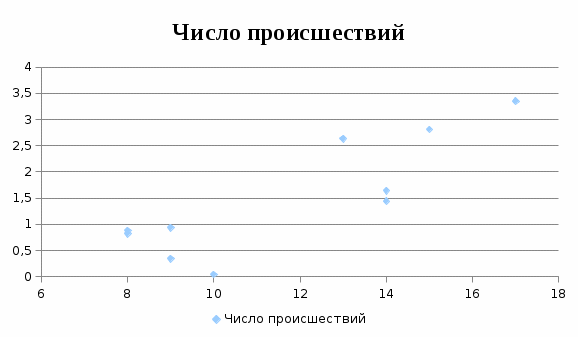 Рисунок 4. – Корреляционное поле для двумерной выборки 2. Выберем две точки: А(9; 0,93) и В(17; 3,35) и определим уравнение линии, проходящей через эти точки. 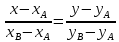 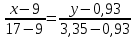 У=0,30х–1,79 3. На основе метода наименьших квадратов параметры а и b оцениваются из условия минимума суммы разностей между фактическими и вычисленными значениями. Реализация этого метода дает следующие формулы для получения оценок параметров уравнения простой линейной регрессии: 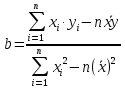 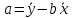 4. Рассчитаем уравнение регрессии в таблице 2.2: Таблица 2.2
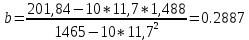 a=1,488-0.2887*11,7=-1,89 Функция регрессии имеет вид У=0,29х-1,89 Воспроизведем диаграмму рассеяния с нанесенной на нее линией регрессии (рисунок 5). 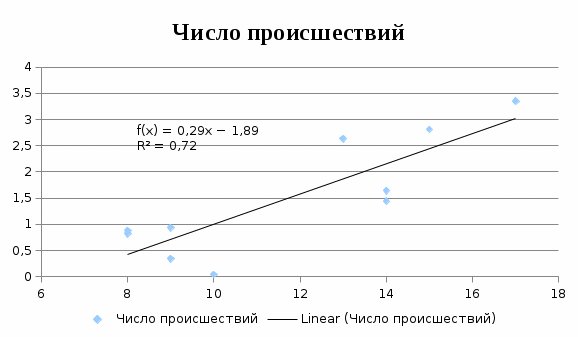 Рисунок 5. Диаграмма рассеяния с нанесенной на нее линией регрессии Связь между переменными является корреляционной (нефункциональной) и измеряется с помощью коэффициента корреляции. Квадрат коэффициента корреляции называется коэффициентом детерминации и определяется из соотношения 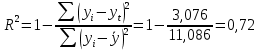 т.е. в 72 % случаев влияет на изменение данных. Другими словами - точность подбора уравнения тренда чуть более 72%. Коэффициент детерминации характеризует долю вариации результативного признака, обусловленную изменчивостью изучаемого фактора. То есть, 72% вариации количества дорожно-транспортных происшествий обусловлена изменением числа водителей моложе 21 года. 5. Оценить тесноту связи можно по величине эмпирического корреляционного отношения, используя формулу 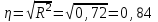 . .Связь между количеством водителей моложе 21 года и числом ДТП с тяжелыми последствиями тесная (более 0,8). Спрогнозируем число ДТП с тяжелыми последствиями для города, в котором число водителей моложе 21 года равно 20% от общего числа водителей. У=0,29х – 1,89 Х = 20%. У=0,29*20 – 1,89 = 3,91 Для города, в котором число водителей моложе 21 года равно 20% от общего числа водителей, количество дорожно-транспортных происшествий составит 3,91 тысяч. Задача №3. Анализ временных рядов и прогнозирование. Сформировать временной ряд для 10 недель. По полученным данным: Спрогнозировать значения индексов на ближайшие две недели, используя метод скользящих средних, выбрав для ее вычисления трехнедельные данные, а также экспоненциальную взвешенную среднюю, выбрав в качестве 0,1, а затем 0,2. Исходные данные.
Решение. 1 Определяем основные показатели временного ряда Абсолютное изменение уровней - в данном случае его можно назвать абсолютным приростом - это разность между сравниваемым уровнем и уровнем более раннего периода, принятым за базу сравнения. Если эта база - непосредственно предыдущий уровень, показатель называют цепным, если за базу взят, например, начальный уровень, показатель называют базисным.Формулы абсолютного изменения уровня: Цепное: Δц = yn – yn-1; Базисное: Δб= yn – yб Если абсолютное изменение отрицательно, его следует называть абсолютным сокращением. Абсолютное изменение имеет ту же единицу измерения, что и уровни ряда с добавлением единицы времени, за которую определено изменение. Без указания единицы времени, за которую произошло измерение, абсолютный прирост нельзя правильно интерпретировать. Таблица 1.1 |