Эконометрика. 1 задача. Решение. Линейное уравнение регрессии имеет вид Параметры уравнения линейной регрессии определим методом наименьших квадратов

• Название: Решение. Линейное уравнение регрессии имеет вид Параметры уравнения линейной регрессии определим методом наименьших квадратов
• Анкор: Эконометрика
• Дата: 18.02.2023
• Размер: 18.18 Kb.
• Имя файла: 1 задача.docx
• Тип: Задача; #943887

Задача

В таблице 16 приведены данные о расходе топлива (у, л на 100 км) автомобиля с двигателем объемом 2 литра с автоматической трансмиссией в зависимости от скорости движения (х, км/ч). В предположении, что между х и у существует линейная зависимость, определить параметры линейной регрессии y  kx  b методом наименьших квадратов. Спрогнозировать расход топлива при скорости 175 км/ч.

Таблица 16

1 Вариант
хi	10	30	40	70	90	110	130	140	150	160
yi	4,5	4,8	5,1	6	7,5	8,1	9	9,8	11,3	14

Решение.

Линейное уравнение регрессии имеет вид: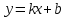



Параметры уравнения линейной регрессии определим методом наименьших квадратов.

Система нормальных уравнений в общем виде: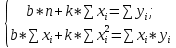



Составим расчетную таблицу для определения параметров уравнения линейной регрессии.

xi	yi	xi*yi	xi2
10	4,5	45	100
30	4,8	144	900
40	5,1	204	1600
70	6	420	4900
90	7,5	675	8100
110	8,1	891	12100
130	9	1170	16900
140	9,8	1372	19600
150	11,3	1695	22500
160	14	2240	25600
∑930	80,1	8856	112300

Система нормальных уравнений с вычисленными коэффициентами: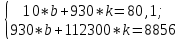



Домножим уравнение (1) системы на (-93), получим систему, которую решим методом алгебраического сложения.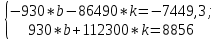



Получаем: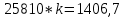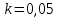





Теперь найдем коэффициент bиз первого уравнения: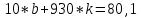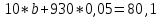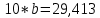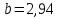









Уравнение линейной зависимости для наших данных принимает вид: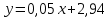



Определим прогнозное значение расхода топлива при скорости 175 км/ч. Для этого в линейное уравнение зависимости подставим значение х_i=175 и получим: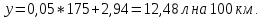



Вывод. В результате анализа зависимости расхода топлива от скорости движения автомобиля было получено линейное уравнение зависимости: 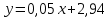. Возможна экономическая интерпретация параметров уравнения линейной регрессии: при увеличении скорости движения автомобиля на 1 км/ч расход топлива увеличивается на 0,05 л на 100 км. Прогнозное значение расхода топлива при скорости движения 175 км/ч составляет 12,48 л на 100 км.