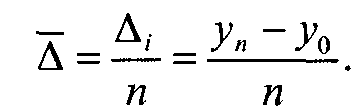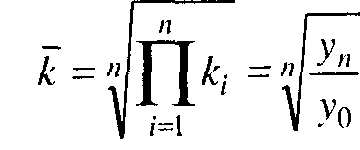статистика двагс вар 20. Задача 1 Описательная статистика. 3
 Скачать 270.94 Kb.
|
Абсолютные и относительные показатели тенденции
В табл. 1.1 абсолютное изменение уровня не является константой тенденции. Оно со временем возрастает, т.е. уровни ряда изменяются с ускорением. Ускорение - это разность между абсолютным изменением за данный период и абсолютным изменением за предыдущий период равной длительности:  Показатель абсолютного ускорения применяется только в цепном варианте, но не в базисном. Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда. 2. Средние показатели данного ряда динамики Средний уровень интервального ряда динамики определяется как простая арифметическая средняя из уровней за равные промежутки времени:
Средний уровень индекса за 10 недель составит 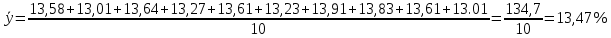 Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения на число усредняемых отрезков времени от базисного до сравниваемого периода:
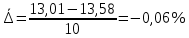 Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте. Если можно пренебречь колеблемостью, то средний темп определяют как геометрическую среднюю из цепных темпов роста за п периодов или из общего (базисного) темпа роста за п периодов:
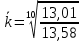 =99,57%3. Спрогнозируем значения данных на ближайшие две недели А) метод скользящей средней состоит в вычислении средней арифметической нескольких ближайших к началу ряда величин. Эта средняя затем используется в прогнозировании на следующий период. Для первых трех недель средняя равна 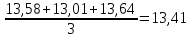 Эта величина может быть использована для прогнозирования индекса на четвертую неделю. Найдем скользящую среднюю сдвинутых трех недель. 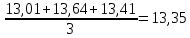 Это значение используем для прогнозирования на пятую неделю. Продолжая этот процесс, получим следующие данные:
В приведенной таблице кроме скользящих средних вычислены ошибки прогнозов и их квадраты. Средний квадрат ошибки определим по формуле 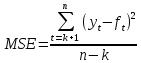 Где ft – прогнозные значения для месяца t; n – объем выборки или длина временного ряда; k – длина усреднения. Чем меньше величина MSE, тем точнее будет прогноз. Кроме того, эта характеристика используется для выбора оптимальной длины усреднения, для чего рассчитываются скользящие средние для разных k и в итоге для прогноза выбирается та модель, которая дает наименьший средний квадрат ошибки. 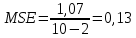 А прогнозное значение на двенадцатую неделю равно 13,45. Рассмотрим модель экспоненциальной взвешенной средней. Экспоненциальное сглаживание – это техника прогнозирования, использующая сглаженные величины временного ряда для вычисления прогнозного значения на следующий период. Модель имеет вид: 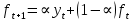 Где α – константа сглаживания (0<α<1). Как видим из модели, для вычисления прогноза на неделю t+1 надо знать величину временного ряда в неделе t и прогнозное значение на эту же неделю. Итак, пусть f1 = y1 = 13,58 и α=0,1. Тогда 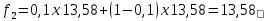 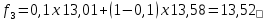 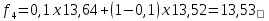 И так далее. Расчетные данные внесем в таблицу.
Итак, прогноз на 12 неделю равен 13,52 и средний квадрат ошибки равен 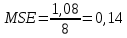 , что больше ошибки при использовании скользящей средней (0,08), а, следовательно, этот прогноз можно признать менее точным.пусть f1 = y1 = 13,58 и α=0,2. Тогда 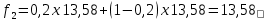 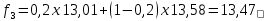 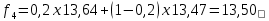 И так далее. Расчетные данные внесем в таблицу.
Итак, прогноз на 12 неделю равен 13,38 и средний квадрат ошибки равен 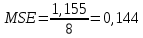 , что больше ошибки при использовании скользящей средней (0,08), а, следовательно, этот прогноз можно признать менее точным.4 Применим метод аналитического выравнивания. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. На практике по имеющемуся временному ряду задают вид и находят параметры функции y=f(t), а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости: линейная, параболическая и экспоненциальная. Метод аналитического выравнивания основан на вычислении значений выровненного ряда по соответствующим математическим формулам. Пусть линия задана уравнением  Для определения параметров надо решить систему уравнений:  В ППП Excel имеется возможность построить линейный тренд. 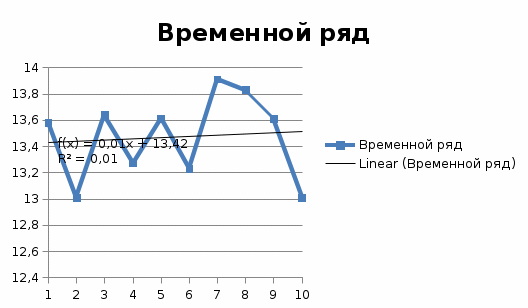 Составим прогноз индекса на 12 неделю: У12 = 0,0095 х 12 +13,418 = 13,53% 4 Вычислим коэффициент автокорреляции В качестве переменной X рассматривают ряд у2, у3, ..., уn в качестве переменной у — ряд у1, у2, ..., уn-1. Тогда приведенная формула для расчета коэффициента корреляции примет вид 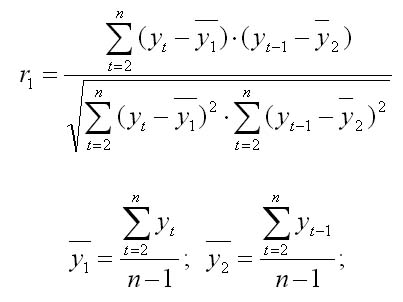 Эта величина - коэффициент автокорреляции первого порядка, так как он определяет зависимость между соседними уровнями ряда t и t-1 Аналогично определяют коэффициенты автокорреляции второго и более высоких порядков. 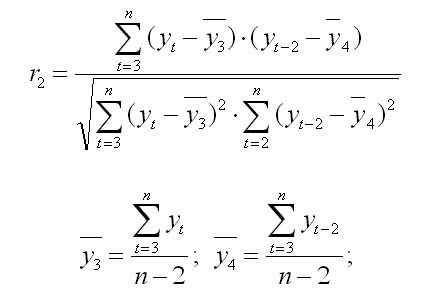 Число периодов, по которым определяется коэффициент автокорреляции, называют лаг автокорреляции. С ростом лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается что лаг должен определяться отношением n/4 - количество наблюдений деленных на 4. Если максимальным оказался коэффициент автокорреляции первого порядка, временной ряд содержит только тенденцию (тренд). Если максимальным оказался коэффициент автокорреляции порядка n, ряд содержит циклические колебания с периодичностью в n моментов времени. Если ни один из коэффициентов автокорреляции не является значимым (близок к 0), можно сказать, что либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит нелинейную тенденцию, для выявления которой проводят дополнительный анализ. Определим коэффициент автокорреляции 1 порядка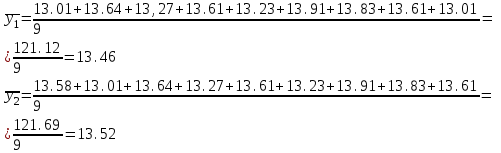 
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
