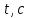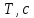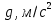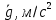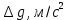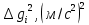Ускорение свободного падения. Лабораторная работа 17 определение ускорения свободного падения
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Лабораторная работа №17 ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ Цель работы: изучить зависимость ускорения свободного падения от географических координат, баллистическим или маятниковым методом экспериментально определить численное значение ускорения свободного падения в Самаре. Краткая теория Вблизи поверхности Земли все свободно падающие тела движутся с одинаковым постоянным ускорением. Ускорение свободного падения  зависит от многих факторов. зависит от многих факторов.если не учитывать вращение Земли вокруг своей оси то  будет зависеть только от гравитационного поля Земли, а если учесть вращение, то, ускорение свободного падения можно представить как векторную сумму двух слагаемых: гравитационного ускорения и центробежного ускорения: будет зависеть только от гравитационного поля Земли, а если учесть вращение, то, ускорение свободного падения можно представить как векторную сумму двух слагаемых: гравитационного ускорения и центробежного ускорения: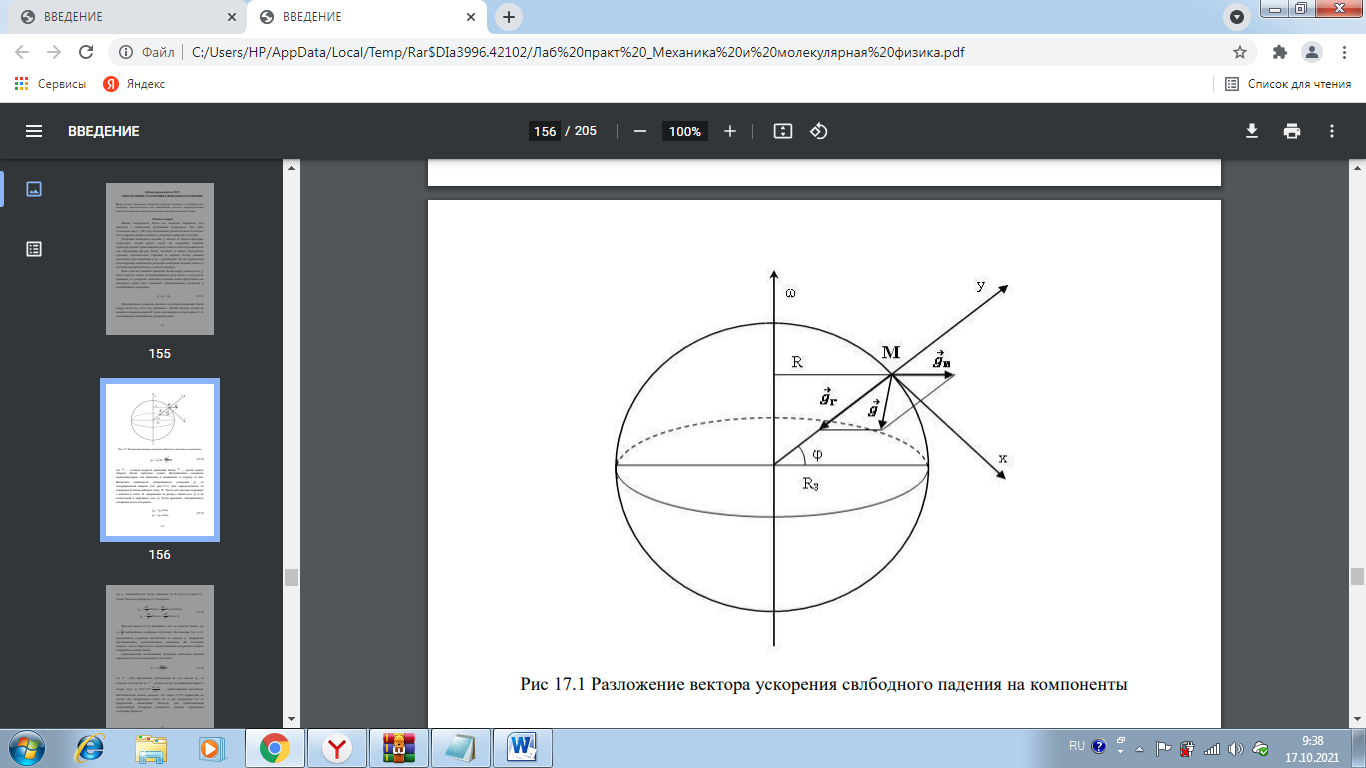 Рис.1. Разложение вектора ускорения свободного падения на компоненты  Центробежное ускорение является следствием вращения Земли вокруг своей оси, из-за чего связанные с Землёй системы отсчёта не являются инерциальными.  где 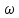 — угловая скорость вращения Земли, — угловая скорость вращения Земли, 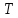 — время одного оборота Земли (звёздные сутки). — время одного оборота Земли (звёздные сутки).Гравитационная составляющая ускорения свободного падения определяется законом всемирного тяготения:  где  – сила притяжения, действующая на тело массой – сила притяжения, действующая на тело массой  , со стороны тела массой , со стороны тела массой  , ,  - радиус-вектор, соединяющий первое и второе тело, - радиус-вектор, соединяющий первое и второе тело, 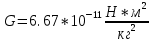 гравитационная постоянная. гравитационная постоянная.Таким образом, для гравитационной составляющей ускорения свободного падения справедлива следующая формула:  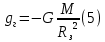 где 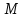 и и  – масса и радиус Земли соответственно. – масса и радиус Земли соответственно.Стандартное («нормальное») значение, принятое при построении систем единиц, составляет  Баллистический метод измерения ускорения свободного падения. Баллистический метод основан на измерении времени падения тела под действием силы тяжести. Если не учитывать сопротивление воздуха, то можно считать, что свободно падающее тело движется равноускорено. Как известно такое движение описывается уравнением 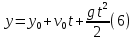 где  – начальная скорость тела, – начальная скорость тела,  – начальная координата тела, – начальная координата тела, 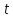 – время падения. Если тело падает из состояния покоя, то несложно догадаться, что – время падения. Если тело падает из состояния покоя, то несложно догадаться, что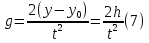 где  - высота падения. - высота падения.Маятниковый метод измерения ускорения свободного падения. Физическим маятником называется любое твердое тело, совершающее колебания относительно единственной оси вращения. Физический маятник, состоящий из материальной точки и невесомой нерастяжимой нити, называется математическим. Его период равен:  где  – длина нити. Отсюда следует, что – длина нити. Отсюда следует, что Для точных измерений пользуются маятником с нитью разной длины. Тогда для двух измеренных периодов маятников  и и  с длинами с длинами  и и  соответственно формула для ускорения свободного падения имеет вид: соответственно формула для ускорения свободного падения имеет вид:  Рис. 2. Схема маятниковой установки Экспериментальная часть Упражнение №2. Схема установки для измерения ускорения свободного падения маятниковым методом приведена на рис.2. Порядок выполнения работы Убедитесь визуально в исправности установки. Запишите в таблицу 1 длину подвеса маятника. Спросите у преподавателя или лаборанта и запишите в таблицу 1 Отклонив грузик на небольшой угол, измерьте время 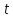 нескольких колебаний. Число колебаний нескольких колебаний. Число колебаний  должно быть больше 15. должно быть больше 15. Вычислите период одного колебания 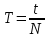 и запишите в таблицу. и запишите в таблицу.Повторите п.п. 3,4 указанное преподавателем число раз. По указанию преподавателя вычислите  по формуле 7. Результат занесите в таблицу. по формуле 7. Результат занесите в таблицу.Вычислите полуширину доверительного интервала  для для  при доверительной вероятности 68% (1,134 – коэффициент Стьюдента при количестве измерений 5 и доверительной вероятности 0,68) занесите результаты в таблицу 1. при доверительной вероятности 68% (1,134 – коэффициент Стьюдента при количестве измерений 5 и доверительной вероятности 0,68) занесите результаты в таблицу 1.Посчитайте абсолютную  и относительную и относительную  погрешность. погрешность.Запишите результат в виде  Результаты измерений и их обработка Таблица 1. Измерение ускорения свободного падения маятниковым методом
Рассчитаем период колебаний: 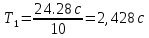 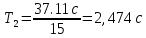  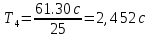  Вычислим ускорение свободного падения:    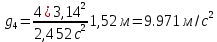 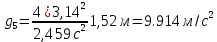 Среднее значение: 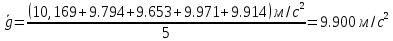 Расчет погрешности измерений Таблица 2. Расчет погрешностей измерений
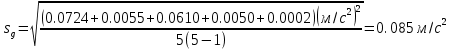  Окончательный результат: 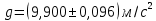 Вывод: в данной лабораторной работе мы изучили зависимость ускорения свободного падения от географических координат, а также маятниковым методом экспериментально определили численное значение ускорения свободного падения в Самаре 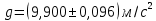 . Полученное значение в пределах погрешности совпадает с теоретическим значением ускорения свободного падения . Полученное значение в пределах погрешности совпадает с теоретическим значением ускорения свободного падения  . Таким образом, опыт можно считать успешным. . Таким образом, опыт можно считать успешным.Контрольные вопросы Как зависит гравитационная составляющая ускорения свободного падения от высоты над поверхностью Земли? Гравитационная составляющая ускорения свободно обратно пропорциональна высоты над поверхностью Земли. На какой широте угол между 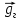 и и 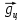 минимальный, а на какой - максимальный? минимальный, а на какой - максимальный? Минимальный угол – на экваторе, максимальный – на полюсах. Выведете формулу (17.15) и докажите, что  , найденное по этой формуле точнее, чем по (17.14). , найденное по этой формуле точнее, чем по (17.14).М 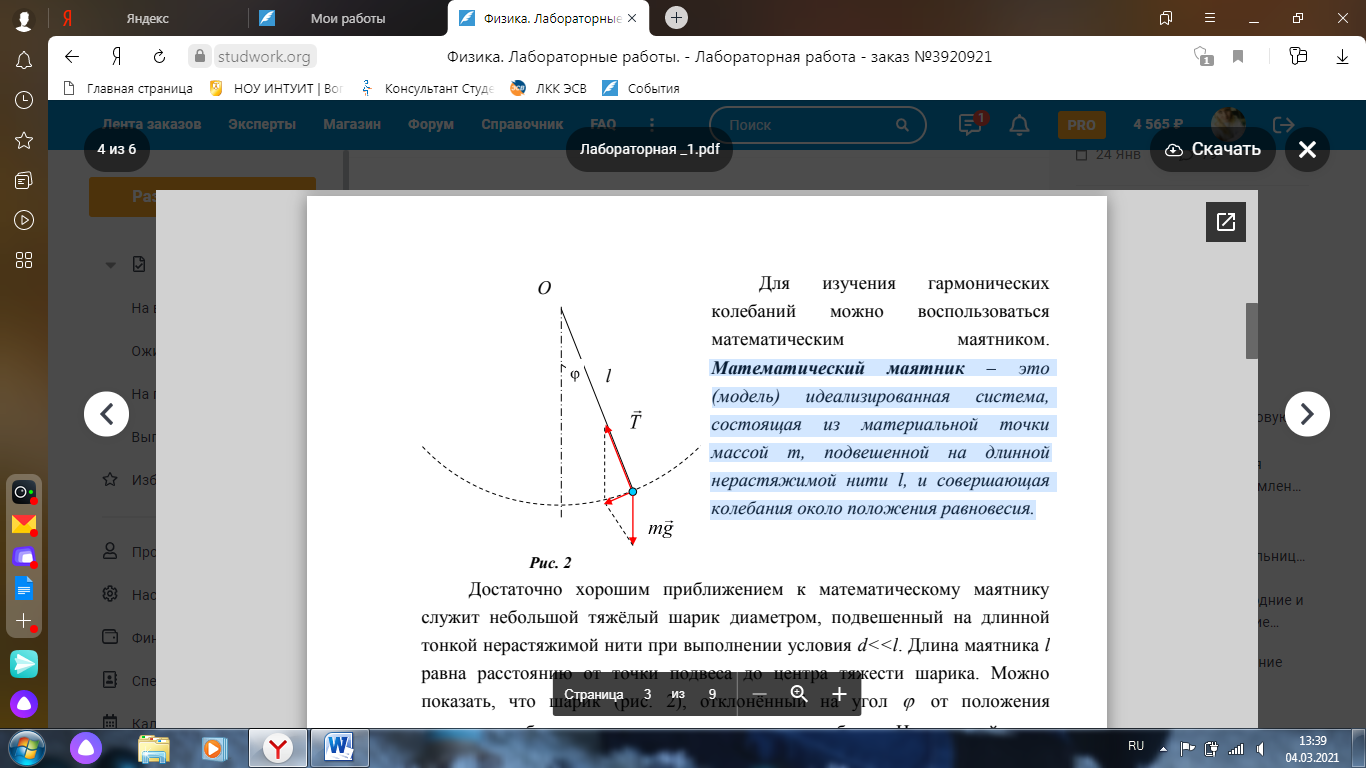 атематический маятник – это (модель) идеализированная система, состоящая из материальной точки массой m, подвешенной на длинной нерастяжимой нити l, и совершающая колебания около положения равновесия. атематический маятник – это (модель) идеализированная система, состоящая из материальной точки массой m, подвешенной на длинной нерастяжимой нити l, и совершающая колебания около положения равновесия.Можно показать, что шарик, отклонённый на угол от положения равновесия, будет совершать гармонические колебания. На него действует возвращающая квазиупругая сила, составляющая силы тяжести. Уравнение динамики вращательного движения для этих условий можно записать в виде 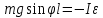 Где  – угловое ускорение; g – ускорение свободного падения. – угловое ускорение; g – ускорение свободного падения.Для малых углов отклонения 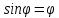 . С учетом того, что для шарика на нити можно принять . С учетом того, что для шарика на нити можно принять 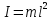 , уравнение движения приобретает вид: , уравнение движения приобретает вид: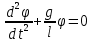 при условии, что собственная частота колебаний системы 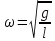 Частным решением последнего дифференциального уравнения является уравнение  Частота ω связана с периодом Т выражением 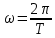 , поэтому период: , поэтому период: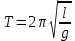 где  – длина нити. Отсюда следует, что – длина нити. Отсюда следует, что Так как мы рассчитываем период колебаний маятника различной длины , тогда 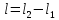  Отсюда получим: 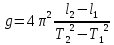 В данном случае величина будет точнее, так как ошибка при определении разности длин и периодов математического маятника , будет меньше, чем при измерении одной длины и определении одного периода. В международной гравиметрической системе IGSN 71 для нормального значения ускорения свободного падения принята формула с поправочными коэффициентами, определёнными по совокупности гравиметрических данных на 1967 г. 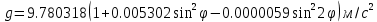 А какие коэффициенты (или формула) получатся у Вас? 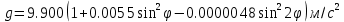 |