РГР по мат моделированию. Коричко КМ-701 14 вар. Федеральное государственное бюджетное образовательное учреждение высшего образования новосибирский государственный технический университет
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра проектирования технологических машин  Дисциплина: «Математическое моделирование технологических машин» Расчетно-графическая работа Вариант 14 Выполнил: Проверил: студент группы КМ-701, МТФ Подгорный Ю. И. Коричко В.В. 22.05.2020 Новосибирск 2020 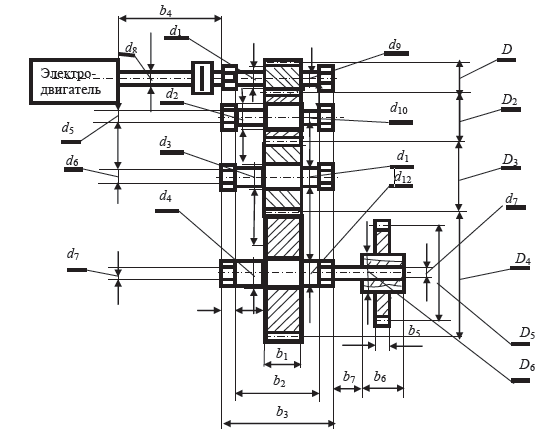 Рисунок 1 – Расчетная схема редуктора Таблица 1 Исходные данные для РГР
Таблица 2 Исходные значения маховых моментов роторов электродвигателей
Нахождение моментов инерции масс. Найдем J12 – момент инерции на первом валу, включающий момент инерции от шестерни. Все остальные значения сведем в табл. 3. На рис. 2 представлена модель шестерни с валом со всеми размерами. Шестерня была рассчитана и построена при помощи прикладной библиотеки КОМПАС 3D. 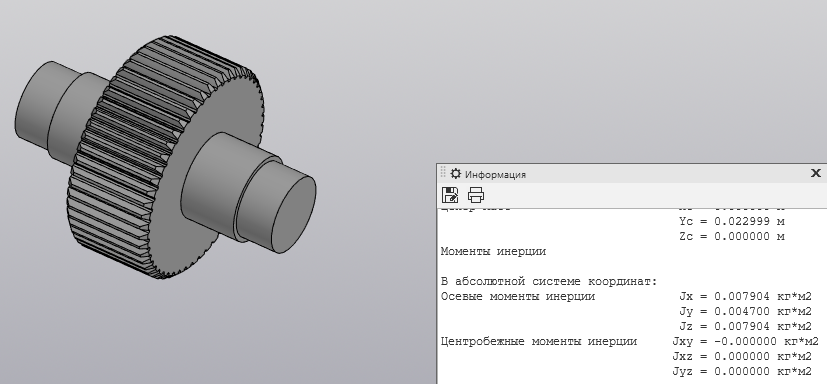 Рисунок 2 – МЦХ первого вала с шестерней Моменты инерции масс были определены при помощи «МЦХ модели». Таким образом, мы можем записать момент инерции первого вала с шестерней относительно оси вращения: 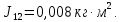 Таблица 3 Моменты инерции масс
Скриншоты остальных валов приведены на рис. 3-7. 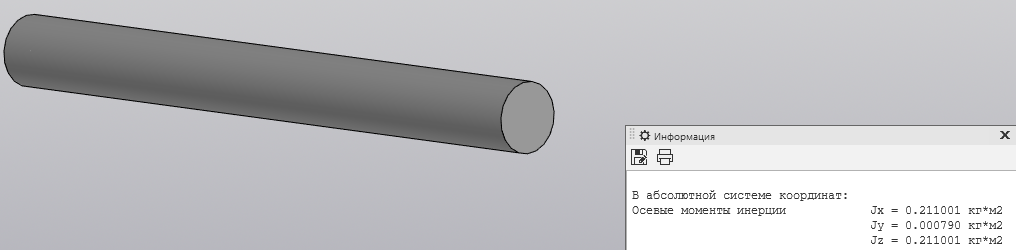 Рисунок 3 – МЦХ первого вала от ротора электродвигателя 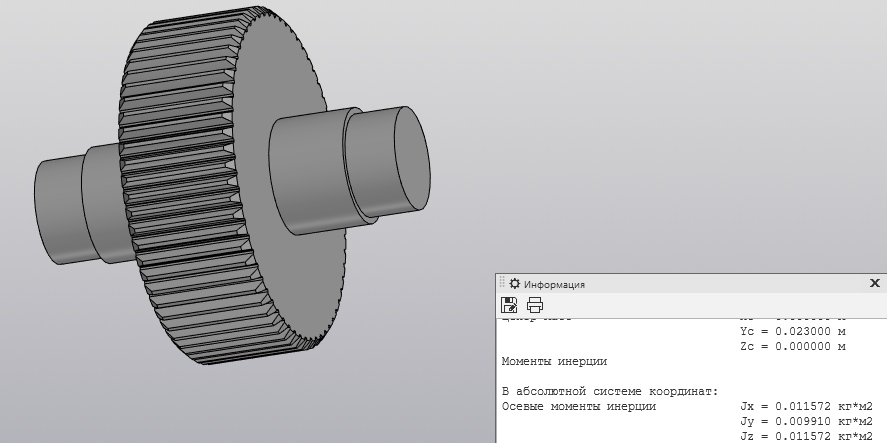 Рисунок 4 – МЦХ второго вала с шестерней 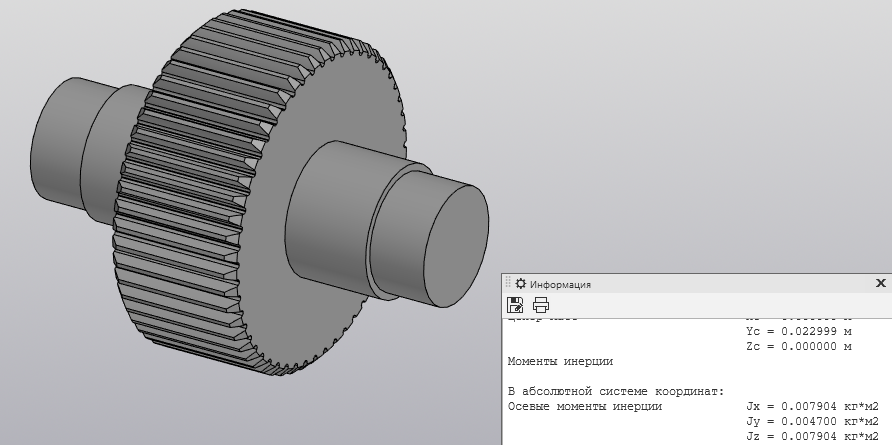 Рисунок 5 – МЦХ третьего вала с шестерней 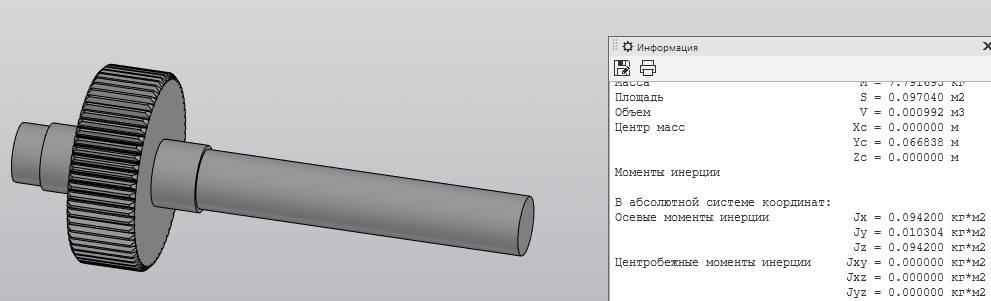 Рисунок 6 – МЦХ первой половины четвертого вала с шестерней 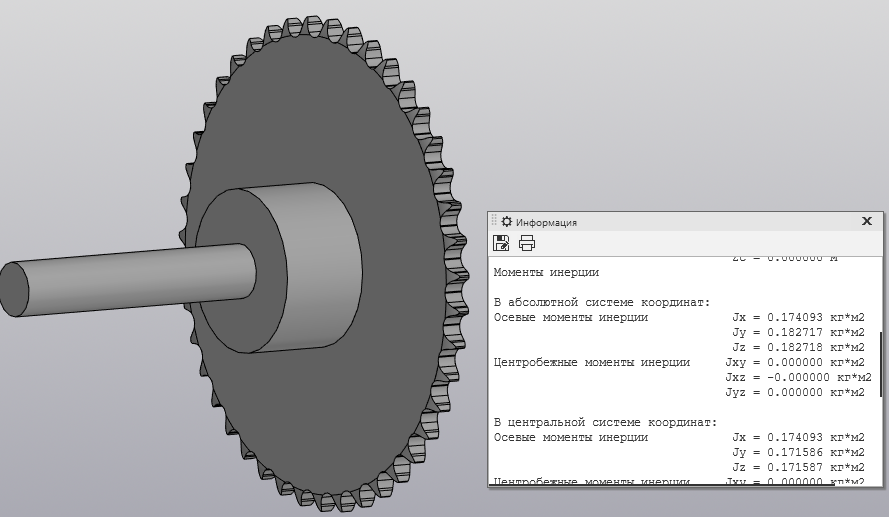 Рисунок 7 – МЦХ второй половины четвертого вала со звездочкой Рассчитаем податливости и жёсткости валов передающих крутящий момент Схемы для определения податливости приведены на рисунках 8 и 9. Мелкой штриховкой показаны области, включённые в расчёт. 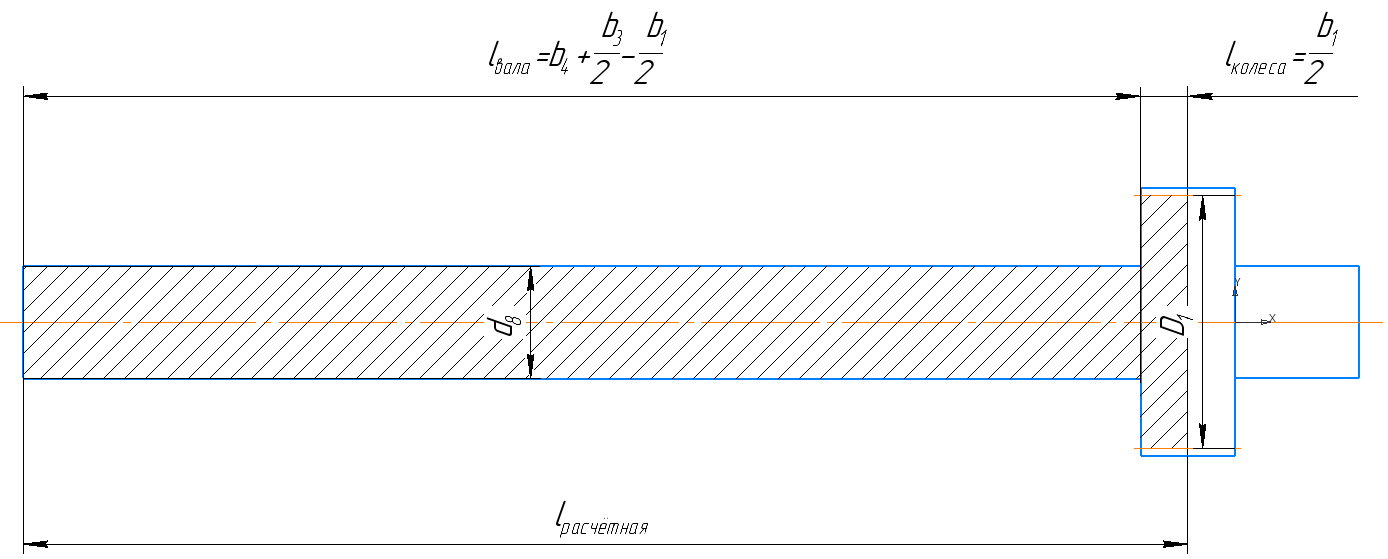 Рисунок 8 – Схема для определения податливости на первом валу  Рисунок 9 – Схема для определения податливости на втором валу Расчёт выполним в Mathcad (рисунок 10).   Рисунок 10 – расчёт податливостей и жёсткостей. Эквивалентная динамическая модель редуктора (рисунок 11) включает в себя моменты инерции масс составляющих элементов и податливости на участках. 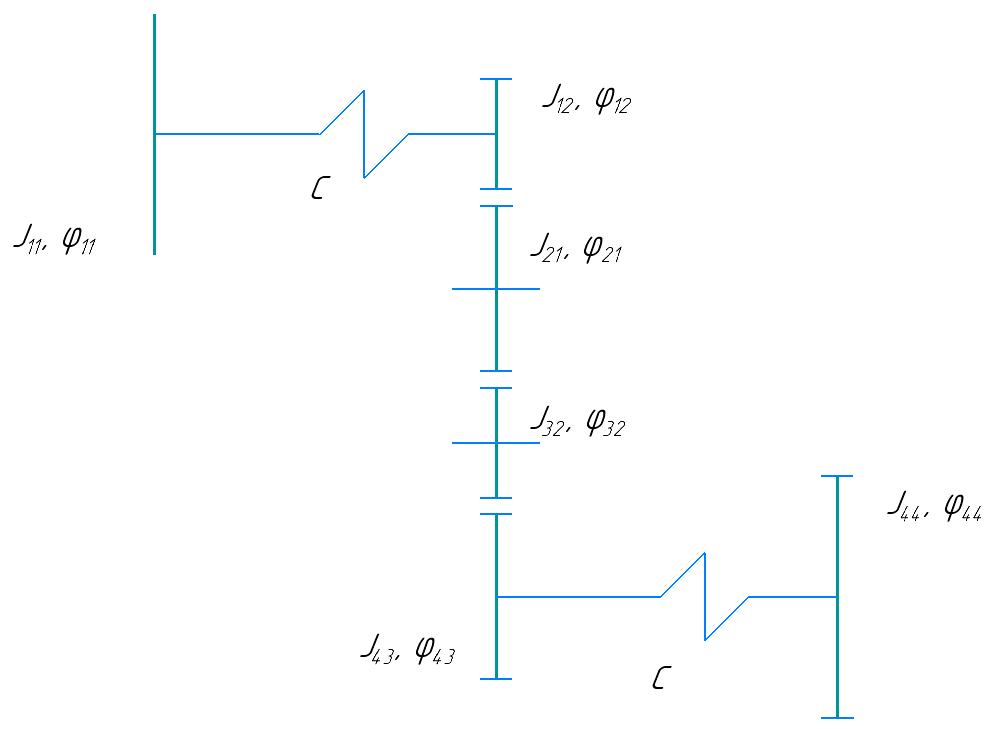 Рисунок 11 – Динамическая модель На рисунке обозначено: J11 – момент инерции на первом валу, включающий момент инерции от ротора электродвигателя, соединительного вала; J12 – момент инерции на первом валу, включающий момент инерции от шестерни; J21 – момент инерции на втором валу, включающий момент инерции от шестерни и вала; J32 – момент инерции на третьем валу, включающий момент инерции от шестерни и вала; J43 – момент инерции на четвертом валу, включающий момент инерции от шестерни и половины четвертого вала; J44 – момент инерции на четвертом валу, включающий момент инерции от звездочки и второй половины четвертого вала; φji – углы поворота соответствующих моментов инерции масс. Определение обобщенных координат Зададимся обобщенной координатой для ротора электродвигателя. Положение ротора определяется его угловой координатой, поэтому φ11 = q1. Положение второго элемента модели также определится угловой координатой, но поскольку момент инерции J12 соединятся с валом электродвигателя размерным валом, то прежде чем шестерня получит импульс на поворот, вал должен будет развернуться на определенный угол, равный величине от деления момента от сил упругости на жесткость. Эту координату обозначим через 2q. В этом случае угловая координата определится по выражению 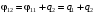 Положение третьего элемента модели определится также угловой координатой. Математически это выражение запишется следующим образом: 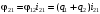 Аналогично для остальных элементов модели обобщенные координаты будут иметь следующие выражения: 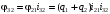 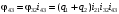 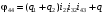 Выражения для кинетической энергии будет иметь вид 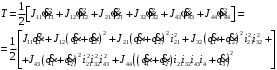 В связи с тем, что нам необходимо иметь представление о кинетической энергии в развернутом виде с обобщенными координатами в том числе их квадратичные и производные первого порядка, то это выражение можно переписать в следующем виде: 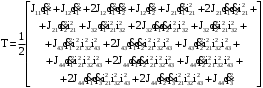 Объединив все члены с 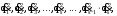 и обозначив постоянные величины через и обозначив постоянные величины через 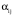 , получим следующие выражения: , получим следующие выражения: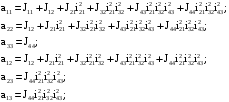 Общий вид выражения для потенциальной энергии для данного механизма будет иметь вид: 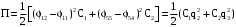 Все обозначения, входящие в это выражение, были приведены ранее. Для составления математической модели механизма воспользуемся уравнением Лагранжа второго рода в обобщенных координатах: 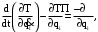 где Т и П – потенциальная и кинетическая энергия; 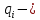 обобщенные координаты. обобщенные координаты.Тогда для частных производных можно будет записать: 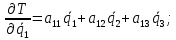 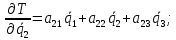 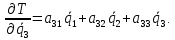 Взяв производные по времени, получим: 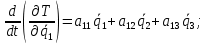 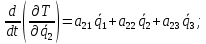 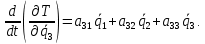 Общее выражение потенциальной энергии для системы, состоящей из трех моментов инерций и двух жесткостей, запишем как: 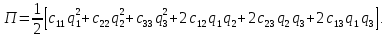 В связи с тем, что потенциальная энергия нашего механизма будет определяться произведением жесткости на квадратичную функцию перемещения, а в нашем случае таких координат две:  и и 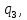 то тогда: то тогда: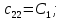 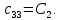 С учетом приведенных выше зависимостей запишем дифференциальные уравнения движений: 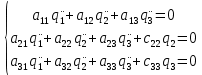 Обозначим 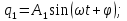 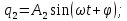 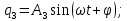 Подставив их в приведенные выше выражения и сократив на 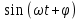 , получим , получим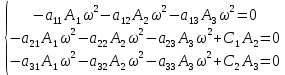 Из первых двух уравнений определим 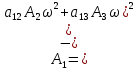 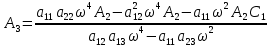 Подставив оба выражения в третье уравнение и произведя преобразования, получим 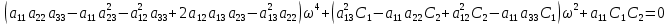 Обозначим 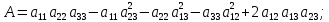 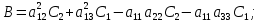 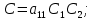 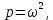 получим 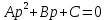 Решив это уравнение, найдем значение корней. Найдём собственные частоты с помощью системы Mathcad (рисунок 12) [2].  Рисунок 12 – Листинг программы Mathcad Исходя из рис.12 значение собственных частот равны 430,697 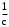 и 414,246 и 414,246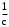 . . Вывод: Найденные собственные частоты системы равны 430,697 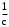 и 414,246 и 414,246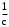 . При заданной мощности 3,5 кВт можно использовать двигатель, например, 132S8/720 с частотой 720 об/мин [1, c.321]. Найдем угловую частоту вращения вала двигателя: . При заданной мощности 3,5 кВт можно использовать двигатель, например, 132S8/720 с частотой 720 об/мин [1, c.321]. Найдем угловую частоту вращения вала двигателя: 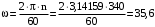 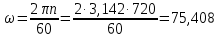 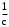 . Это значит, что данный двигатель можно использовать в этой системе без появления резонанса. Выбор другого двигателя не требуется. . Это значит, что данный двигатель можно использовать в этой системе без появления резонанса. Выбор другого двигателя не требуется. Библиография Дунаев П.Ф. Конструирование узлов и деталей машин / П.Ф. Дунаев, О.П. Леликов. – М.: Академия, 2010. – 447 с. Подгорный Ю.И. Математическое моделирование технологических машин: учебное пособие / Ю.И. Подгорный, В.Ю. Скиба, Т.Г. Мартынома.- Новосибирск: Изд-во НГТУ, 2017.-87 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 м2
м2