механика. Решение На схеме 3 ступени Зубчатая цилиндрическая с внешним зацеплением(1 и 2)
 Скачать 269.88 Kb.
|
 Практическое задание 1Вариант 23 Дано:  Решение: На схеме 3 ступени: Зубчатая цилиндрическая с внешним зацеплением(1 и 2;) Зубчатая цилиндрическая с внешним зацеплением(2_и 3; 5 и 5_) Планетарная передача (6 и 6_ и 7 ; 4 и 3_) Находим передаточные отношения механизма: 1)зубчатая передача с внешним зацеплением U1=z2/z1=26/25=1,04 2) зубчатая передача с внешним зацеплением: U2=(z2_/z3)*(z5/z5_)=1*0,96=0,96 3)Планетарная передача U3=1-(z6/z6_/z7)*(z4/z3)=1-(0,025)*1=1-0,02=0,975 Общее передаточное отношение: U=U1*U2*U3=1,04*0,96*0,975=0,973 Угловая скорость ведомого звена:   Угловое ускорение: Общий КПД:  Практическое задание 2 Тип 2 Вариант 23  Дано: Решение: Определим частоту вращения тихоходного вала  Определим требуемую мощность электродвигателя:  Предварительное определение частот вращения вала электродвигателя и быстроходного вала редуктора  Выбор электродвигателя 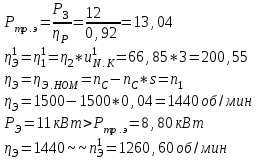 Геометрические параметры электродвигателя:  Определение фактического значения передаточного числа U редуктора   Определение мощности P на быстроходном валу   Определение крутящих моментов на валах редуктора  
Расчет зубчатой передачи Для расчёта конической зубчатой передачи используются следующие данные: крутящий момент на быстроходном валу редуктора  ; частота вращения шестерни  ; частота вращения колеса  ; передаточное число редуктора ; срок службы привода L = 5 лет; коэффициент суточной загрузки К сут = 0,3; коэффициент годичной загрузки К год = 0,6; характер нагрузки – постоянный; режим работы – лёгкий. Расчёт выполнен по рекомендациям и формулам методического пособия 4.1 Выбор материала и термообработки зубчатых колёс При проектировании редукторов рекомендуется назначать для шестерни и колеса сталь одной и той же марки, но обеспечивать соответствующей термообработкой твёрдость поверхности зубьев шестерни на 20 – 30 единиц Бринелля выше, чем колеса. Как правило, применяют термообработку – улучшение. При таком виде термообработки механические характеристики стали снижаются с увеличением диаметра заготовки. В этом случае шестерня будет иметь более высокие механические характеристики по сравнению с колесом. Заготовки для зубчатых колёс получают ковкой, штамповкой и литьем. Согласно этим рекомендациям предполагая, что диаметр заготовки для шестерни не выше 90 мм, а для колеса свыше 120 мм, принимаем: а) для шестерни 1 – сталь 45; термообработка – улучшение; предел прочности σВ = 780 МПа; предел текучести σТ = 440 МПа; твёрдость НВ1 = 230; б) для колеса 2 – сталь 45; термообработка – улучшение; предел прочности σВ = 690 МПа; предел текучести σТ = 340 МПа; твёрдость НВ2 = 195. Термообработка (улучшение) характеризуется хорошей прирабатываемостью зубьев колёс и сохранением во времени точности, полученной при механической обработке. 4.2 Определение допускаемых напряжений 4.2.1 Определение допускаемых контактных напряжений Допускаемые контактные напряжения [σН] определяют раздельно для шестерни и колеса по формуле  , где σHlimb – предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов перемены напряжений, МПа; SH – коэффициент безопасности; KHL – коэффициент долговечности. Значения σHlimb и SH определяют в зависимости от группы стали и термообработки. Для стальных колёс с термообработкой (улучшение) и средней твёрдости поверхностей зубьев НВ ≤ 350 предел контактной выносливости поверхности зубьев σHlimb определяют по формуле σHlimb = 2·НВ + 70. Используя эту формулу, определим пределы контактной выносливости σHlimb1, σHlimb2 поверхностей зубьев соответственно для шестерни и колеса: σHlimb1 = 2·НВ1 + 70; σHlimb1 = 2·230 = 530 МПа; σHlimb2 = 2·НВ2 + 70; σHlimb2 = 2·195 = 460 МПа. По известной рекомендации [4, с. 15, таблица 2.3] для стальных колёс с термообработкой (улучшение) и средней твёрдости поверхностей зубьев НВ ≤ 350 коэффициент безопасности SH = 1,1. Величину коэффициента долговечности KHL определим по формуле  где NHO – базовое число циклов перемены напряжений; NHE – эквивалентное число циклов перемены напряжений. Базовое число NHO циклов перемены напряжений определяют в зависимости от твёрдости стали. При твёрдости НВ < 200 принимают NHO = 10·10^6 циклов. При твёрдости НВ > 200 значение NHO возрастает по линейному закону. В проектируемом приводе имеем: твёрдость шестерни НВ1 = 230; твёрдость колеса НВ2 = 195. График изменения величины NHO в зависимости от твёрдости НВ поверхности зубьев приведён в работе [4, с. 16]. Согласно этому графику определим базовые числа NHO1, NHO2 перемены напряжений соответственно для шестерни и колеса: NHO1 = 13,5·10^6 циклов; NHO2 = 10·10^6 циклов. При постоянной нагрузке эквивалентное число циклов перемены напряжений NHE равно суммарному числу циклов перемены напряжений NΣ для зубчатого колеса за срок службы. Величину NΣ для зубчатого колеса с частотой вращения n за t часов работы определим по формуле  Время t работы проектируемого привода в часах определим по формуле  где Ксут, Кгод – коэффициенты соответственно суточной и годовой загрузки; L – срок службы передачи в годах. По условию задания для проектирования имеем: Ксут = 0,3; Кгод = 0,6; L = 5 лет. Тогда t = 24·0,3·365·5·0,6 = 7884 ч. Формула для определения суммарного числа циклов перемены напряжений для шестерни имеет вид  Тогда  циклов.Формула для определения суммарного числа циклов перемены напряжений для колеса принимает вид Тогда  цикловТак как режим работы привода постоянный, то эквивалентное число NHE циклов перемены напряжений равно суммарному числу NΣ циклов перемены напряжений:  Согласно этой рекомендации имеем: а) для шестерни = = 681,18·10^6 циклов; = 13,5·10^6 циклов; б) для колеса = 316,27·10^6 циклов;  = 10·106 циклов. Если выполняется условие  ≥ , то принимают  = 1.Из проведённого расчёта имеем: а) для шестерни  = 681,18·10^6 циклов > = 13,5·10^6 циклов;б) для колеса  = 198,77·10^6 циклов > = 10·10^6 циклов.Так как для шестерни 1 и колеса 2 редуктора последнее условие выполнено, то принимаем KHL = 1. Тогда допускаемые контактные напряжения [σН1], [σН2] соответственно для шестерни 1 и колеса 2, вычисляемые по формуле (4.1), равны:     В качестве допускаемого контактного напряжения принимается допускаемое напряжение того зубчатого колеса, для которого оно меньше. Поскольку [σН2] < [σН1], то в качестве допускаемого контактного напряжения [σН] принимаем допускаемое контактное напряжение [σН2] колеса 2: [σН] = [σН2] = 418,18 МПа. 4.2.2 Определение допускаемых напряжений изгиба Согласно ГОСТ 21354–75 при расчёте на выносливость при изгибе зуб рассматривают как балку, защемлённую одним концом. Силу считают приложенной к вершине зуба по нормали к его поверхности; силу трения не учитывают. Допускаемое напряжение изгиба [σF] определяют раздельно для шестерни и колеса по формуле  где σFlimb – предел выносливости зуба при изгибе, соответствующий базовому числу циклов перемены напряжений, МПа; SF – коэффициент безопасности; KFL – коэффициент долговечности. Для всех сталей ГОСТ 21354–75 принимает базовое число циклов  Поскольку эквивалентное числе циклов NFЕ перемены напряжений больше базового (NFЕ > NFО), то коэффициент KFL принимают равным единице. Последнее условие соответствует нашему случаю, так как NFЕ = NНЕ. Поэтому принимаем  = 1. По известной рекомендации для стальных колёс с термообработкой – улучшение и средней твёрдости поверхностей зубьев НВ<350 коэффициент безопасности  Предел выносливости зубьев при изгибе σFlimb, соответствующий базовому числу циклов перемены напряжений (NFO = 4·10^6 циклов) для стальных колёс с соответствующей термообработкой (улучшение) и твёрдостью зубьев НВ = 180 – 350 вычисляют по формуле σFlimb = 1,8·НВ. Определим по формуле пределы выносливости зубьев при изгибе σFlimb1, σFlimb2 соответственно для шестерни и колеса: σFlimb1 = 1,8·НВ1; σFlimb1 = 1,8·230 = 414 МПа; σFlimb2 = 1,8·НВ2 ; σFlimb2 = 1,8·195 = 351 МПа. Тогда допускаемые напряжения изгиба [σF1], [σF2] соответственно для шестерни 1 и колеса 2 будут равны:     4.3 Выбор угла наклона зубьев Согласно заданию необходимо спроектировать коническую передачу, зубчатые колёса которой имеют круговые зубья. Круговые зубья располагаются по дуге окружности, по которой движется инструмент при нарезке зубьев За расчётный угол принимается угол βm на окружности среднего делительного диаметра dm колеса. Угол βm наклона зуба для круговых зубьев рекомендуется по ГОСТ 19326–73 принимать в пределах 30 – 40 градуса . Используя эту рекомендацию, принимаем среднее значение этого угла 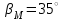 4.4 Выбор коэффициента ширины зубчатого венца колеса Коэффициент ψ bd ширины зубчатого венца численно равен отношению ширины b зубчатого венца к среднему делительному диаметру dm1 шестерни:  Для колёс при твердости зубьев НВ ≤ 350 и постоянной нагрузке рекомендуют [4, с. 18] принимать значение  ≈ 0,5 – 0,6.Проектируемая передача соответствует этой рекомендации, поэтому принимаем = 0,54.5 Проектировочный расчёт на контактную прочность Проектировочный расчёт на контактную прочность проводится с целью предотвращения преждевременного выхода из строя конических зубчатых колёс из-за разрушения их активных поверхностей в результате усталостного выкрашивания. В ходе проектировочного расчёта предварительно определяются геометрические параметры зубчатой передачи. 4.5.1 Определение предварительного значения среднего делительного диаметра dm1 шестерни Известные данные для расчёта: Т1 = 76,4 Н·м; U = 21,54; ψ bd = 0,5; [σН] = 418,18 МПа. Предварительное значение среднего делительного диаметра dm1 шестерни определим по формуле  где Kd – вспомогательный коэффициент; Т1 – крутящий момент на валу шестерни, Н·м; KHβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; U – передаточное число; ψ bd – коэффициент ширины зубчатого венца; [σН] – допускаемое контактное напряжение. Для передач с непрямыми зубьями [4] принимают значение вспомогательного коэффициента  Значение коэффициента, учитывающего неравномерность распределения нагрузки по ширине венца, определяют по графикам в зависимости от твёрдости НВ зубьев, коэффициента ψ bd ширины зубчатого венца и схемы передачи. При твёрдости зубьев НВ ≤ 350, величине ψ bd = 0,5 и расположении валов колёс в конических подшипниках принимают KHβ = 1,15. Таким образом, значения всех величин, входящих в правую часть выражения определены. Проведя вычисления, получим  4.5.2 Определение ширины зубчатого венца Известные данные для расчёта: dm1 = 65,64 мм; ψ bd = 0,5. Ширину b зубчатого венца определим по зависимости, полученной из формулы  Вычисленное значение b округлим до ближайшего целого числа. b = 35 мм. Определение внешнего окружного модуля Известные данные для расчёта: b = 35 мм. Внешний окружной модуль mte определим по формуле  . 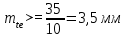Вычисленное значение окружного модуля mte округлим до ближайшего значения по ГОСТ 9563–, отдавая предпочтение первому ряду: mte = 3,5 мм. 4.5.4 Определение предварительных значений углов делительных конусов Известные данные для расчёта: U = 21,54. Предварительные значения углов δ2, δ1 делительных конусов соответственно колеса 2 и шестерни 1 определим по формулам:  ;  Проведя вычисления по формулам (4.11), (4.12) с точностью до минуты, получим   4.5.5 Определение предварительного значения внешнего делительного диаметра de1 шестерни Известные данные для расчёта: dm1 = 70,875 мм; b = 35 мм; δ1 ’ = 2,7 . Предварительное значение внешнего делительного диаметра de1 шестерни определим по формуле  .Все величины, входящие в правую часть выражения известны. Проведя вычисления, получим  4.5.6. Определение чисел зубьев z1, z2 шестерни и колеса Известные данные для расчёта: de1 = 85,575 мм; mte = 3,5 мм; U = 21,54. Числа зубьев z1, z2 шестерни и колеса определим по формулам: .  Проведём вычисления по формулам (4.14), (4.15):  Полученное значение z1 округлим до ближайшего целого числа: z1 = 24.  Полученное значение z2 округлим до ближайшего целого числа: z2 = 517. По выбранным значениям чисел зубьев z1, z2 шестерни 1 и колеса 2 уточним значение передаточного числа U конической передачи: U = z2/ z1 = 517/24 = 21,5 Значение U = 21,54 будем использовать в последующих расчётах. 4.5.7 Определение основных геометрических параметров передачи Известные данные для расчёта: mte = 3,5 мм; z1 = 24; z2 = 517; b = 35 мм; βm = 35 . Основные размеры конических зубчатых колёс с межосевым углом Σ = 90 определим по формулам Внешнее конусное расстояние Re:  Среднее конусное расстояние Rm:  Углы δ1, δ2 делительных конусов соответственно шестерни и колеса:  Внешние делительные диаметры de1, de2 соответственно шестерни и колеса:  Средние делительные диаметры dm1, dm2 соответственно шестерни и колеса:  Средний нормальный модуль   Внешняя высота hae головки зуба  Внешняя высота hfe ножки зуба  Внешняя высота he зуба  Внешние диаметры dae1, dae2 вершин соответственно шестерни и колеса:  Угол θa головки зуба θa  Угол θf ножки зуба θf  Углы δa1, δa2 конусов вершин соответственно шестерни и колеса:  Углы δf1, δf2 конусов впадин соответственно шестерни и колеса:  4.6 Определение окружной скорости V зубчатых колёс Известные данные для расчёта: dm1 = 82, 32 мм; n1 = 1440 об/мин. Окружную скорость V зубчатых колёс определим по формуле  где dm1 – средний делительный диаметр шестерни, мм; n1 – частота вращения шестерни, об/мин. Проведя вычисления по формуле получим .  м/c4.7 Выбор степени точности зубчатых колёс Степень точности зубчатых колёс выбирается в зависимости от окружной скорости V и формы зубьев Так как передача имеет круговые зубья и окружная скорость V = 6,2 м/с, то степень точности – 8. Такая степень точности колёс применяется для передач в общем машиностроении. 4.8 Проверочные расчёты зубчатой передачи По результатам предварительных расчётов уточнено передаточное число U редуктора (было U = 21,54, стало U = z2/z1 = 517/24 = 21,54) и определены геометрические параметры шестерни 1 и колеса 2. Поэтому необходимо провести проверочные расчёты зубчатой передачи. 4.8.1 Расчёт на контактную выносливость Известные данные для расчёта: U = 21,54; dm1 = 82,32 мм; ; b = 35 мм; Т1 =76,4 Н·м; V = 6,2 м/с; Rm = 500 мм. Формула проверочного расчёта имеет вид  где σН, [σН] – соответственно действительное и допускаемое контактные напряжения, МПа; zH – коэффициент, учитывающий форму сопряженных зубьев; zМ – коэффициент, учитывающий механические свойства материалов сопряжённых зубчатых колёс; zε – коэффициент, учитывающий суммарную длину контактных линий; ωHt – удельная расчётная окружная сила, Н/мм; dm1 – средний делительный диаметр шестерни 1, мм; U – передаточное число зубчатой передачи. Значения U и dm1 в формуле (4.17) известны. Определим остальные величины в правой части этой формулы. При угле зацепления α = 20 о и зубчатых колёс без смещения величину коэффициента zH определим по формуле  Для стальных зубчатых колёс величину коэффициента zМ по рекомендации принимаем  Для конических зубчатых колёс величину коэффициента zε ,учитывающего суммарную длину контактных линий, определим по формуле  где εa – коэффициент торцевого перекрытия, определяемый по формуле  Тогда коэффициент zε , учитывающий суммарную длину контактных линий, будет равен zε = 1,32 1 = 0,87. Удельную окружную расчётную силу ωHt определим по формуле  где Ft – окружная сила, Н; b – ширина зубчатого венца, мм; KHβ – коэффициент, учитывающий распределение нагрузки по ширине венца; KHV –коэффициент, учитывающий возникающую в зацеплении динамическую нагрузку. Окружную силу Ft определим по формуле  где T1 – крутящий момент на шестерне 1; dm1 – средний делительный диаметр шестерни. Вычислим значение окружной силы на шестерне:  Значение коэффициента KHβ, учитывающего неравномерность распределения нагрузки по ширине венца, определяют по графикам] в зависимости от твёрдости НВ зубьев, коэффициента ψ bd ширины зубчатого венца и схемы передачи. При консольном расположении зубчатого стального колеса с твердостью зубьев НВ ≤ 350, значении коэффициента ширины зубчатого венца ψ bd = 0,5 и расположении валов колёс в конических подшипниках принимают KHβ = 1,15. Величину коэффициента KHV , учитывающего возникающую в зацеплении динамическую нагрузку в зацеплении, определим по формуле  где ωHV – удельная окружная динамическая сила, Н/мм; ωHtp – удельная расчётная окружная сила в зоне её наибольшей концентрации, Н/мм. Удельную окружную динамическую силу ωHV определим по формуле 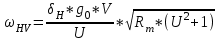 где δН – коэффициент, учитывающий влияние вида зубчатой передачи; go – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; V – окружная скорость; Rm – среднее конусное расстояние; U – передаточное число зубчатой передачи. Величины V, Rm, U, входящие в правую часть выражения (4.24), определены ранее. При твёрдости поверхностей НВ < 350 и непрямых зубьях величина этого коэффициента равна δН = 0,002. Для зубьев с внешним окружным модулем mte≤ 3,5 и степени точности 8 колеса значение этого коэффициента go = 56. Значения всех величин, входящих в правую часть формулы, определены. Вычислим значение окружной динамической силы:  Удельную расчётную окружную силу ωHtp в зоне её наибольшей концентрации определим по формуле Тогда величина коэффициента KHV,  учитывающего динамическую нагрузку в зацеплении, будет равна  Вычислим удельную окружную расчётную силу по формуле  Вычислим действительное контактное напряжение по формуле  При проверочном расчёте зубчатой передачи действительные контактные напряжения σН не должны превышать допускаемые контактные напряжения [σН] более чем на 5 %. В проведённом расчёте это условие выполняется: σН = 485 МПа < [σН] = 500 МПа. 4.8.2 Расчёт на выносливость по напряжениям изгиба Известные данные для расчёта: z1 = 24; z2 = 1809,5; βm = 35 ;  ;  Оценим предварительно относительную прочность зубьев шестерни и колеса. При расчёте конических колёс с круговыми зубьями их заменяют биэквивалентными цилиндрическими прямозубыми колесами. Для этого круговые зубья приводятся к прямым, а конические колёса – к цилиндрическим. Определим числа зубьев zvn1, zvn2 биэквивалентных прямозубых шестерни и колеса по формулам  где βm – угол наклона зуба Для шестерни  Для колеса  Далее по графику [выберем коэффициенты YF1, YF2 формы зубьев соответственно шестерни и колеса. YF1 = 3,7; YF2 = 3,6. Определим соотношения  ,  для шестерни и колеса: Меньшее значение из полученных значений этих соотношений определяет меньшую прочность зуба по напряжениям изгиба. Так как зуб колеса менее прочен по сравнению с зубом шестерни, то проверку выносливости на изгиб проводим только по зубу колеса. Условие прочности зуба по напряжениям изгиба (в предположении, что в зацеплении находится одна пара зубьев) выражается формулой  где σF, [σF] – соответственно действительное и допускаемое напряжения изгиба, МПа; YF – коэффициент формы зуба колеса (YF = YF2); Yβ – коэффициент, учитывающий наклон зуба; mnm – средний нормальный модуль, мм; ωFt – удельная расчётная окружная сила, Н/мм. Величину коэффициента Yβ определим по формуле  Удельную расчётную окружную силу ωFt определим по формуле  где KFβ – коэффициент, учитывающий распределение нагрузки по ширине венца; KFV – коэффициент, учитывающий динамическую нагрузку в зацеплении. Величина коэффициента KFβ зависит от твёрдости зубьев, коэффициента ψ bd , ширины зубчатого венца и схемы зубчатой передачи. По графику, приведенному в работе для твёрдости зубьев HB ≤ 350 и коэффициенте ширины зубчатого венца ψ bd = 0,5 имеем KFβ = 1,3. Величину коэффициента KFV определим по формуле  где ωFV – удельная окружная динамическая сила, Н/мм; ωFtp – удельная расчётная окружная сила в зоне её наибольшей концентрации, Н/мм. Величину удельной окружной динамической силы определим по формуле  где δF – коэффициент, учитывающий вид зубчатой передачи. Для передач с непрямыми зубьями принимают δF = 0,006. Остальные величины в формуле определены ранее. Величина удельной окружной силы равна  Величину удельной расчётной окружной силы ωFtp в зоне её наибольшей концентрации определим по формуле  Численное значение расчётной окружной силы равно Величина коэффициента KFV, учитывающего динамическую нагрузку в зацеплении, равна  Величину удельной расчётной окружной силы ωFt вычислим по формуле  Вычислим величину действительного напряжения изгиба на зубе колеса:  Из проведённого расчёта видно, что действительное напряжение σF = 108,68 МПа < [σF2] = 200,57 МПа. Это означает, что условие изгибной прочности соблюдается. 4.9 Определение усилий в зацеплении данные для расчёта: βm = 35 ; δ1 = 2,63 ; α = 20о ; dm1 = 82,32 мм; Т1 = 76,4 Н·м. Силы взаимодействия между зубьями шестерни и колеса задают в виде составляющих по осям координат. В зацеплении конических зубчатых колёс действуют окружные Ft , радиальные Fr и осевые Fa силы, приложенные в полюсе зацепления П на средней делительной окружности. Схема сил в зацеплении конической передачи приведена на рисунке 4.3. На рисунке шестерня и колесо условно разнесены. Окружные силы Ft1 , Ft2 соответственно шестерни и колеса определим по формуле  где Т1, dm1 – соответственно крутящий момент на валу шестерни и средний делительный диаметр шестерни.  Для шестерни окружная сила направлена по направлению вращения, а для колеса – против направления вращения. Направления осевых сил в передаче с круговыми зубьями зависят от направления вращения шестерни и направления линии наклона зуба, которые определяют при наблюдении с вершины конуса. Для расчёта радиальных Fr1, Fr2 и осевых Fa1, Fa2 сил на шестерне и колесе принимаем, что направление вращения шестерни происходит против хода часовой стрелки, а направление наклона зуба шестерни – правое. При таких условиях радиальную силу Fr1 определим по формуле  Осевую силу на шестерне Fa1 определим по формуле  При принятых выше условиях осевая сила Fо1 , приложенная к шестерне, направлена от вершины конуса к основанию, а радиальная сила Fa1 направлена к её оси. Осевая сила Fa2 на колесе по модулю равна радиальной силе Fr1 на шестерне, направления этих сил противоположные: Fa2 = Fr1 = 804,3 Н. Радиальная сила Fr2 на колесе по модулю равна осевой силе Fa1 на шестерне, но имеет противоположное направление: Fr2 = Fa1 = 806,6 | ||||||||||||||||
76,4 Н*М
1709 Н*М