Маурер вар. 66 С1. Задание С1 Определение реакций опор балки
 Скачать 0.75 Mb.
|
|
Ошибки1: Задание С1 Определение реакций опор балки Конструкция, состоящая из двух прямолинейных стержней, жестко скрепленных между собой в точке С, расположена в вертикальной плоскости. На конструкцию действует пара сил с моментом М = 50 кН∙м, распределенная нагрузка интенсивности q = 10 кН/м, приложенная к участку HB вертикально вниз, и одна сосредоточенная сила F=10кН, приложенная к точке D под углом 15. При расчетах размер а принять равным 0,5 м. Для данной конструкции определить реакции связей конструкции; выяснить: − присутствует ли среди реакций связей изучаемой конструкции реакция в виде момента пары сил, и, если такая реакция имеется, то выполнить пункт 3, − если указанная реакция связи в виде момента пары сил отсутствует, то выяснить, в какой точке конструкции известно точное направление полной реакции связи в виде силы и для этой реакции выполнить пункт 4; определить, при каком значении угла αi, образуемого указанной в варианте задания сосредоточенной силой Fi с координатной осью, реакция в виде момента пары сил будет иметь минимальное по модулю значение, и для этого значения угла αiнайти все остальные реакции связей; для выбранной полной реакции связи в виде силы найти, при каком значении угла αi образуемого сосредоточенной силой Fiс указанной в варианте задании координатной осью данная реакция будет иметь минимальное по модулю значение, и для этого значения угла αiнайти все остальные реакции связей. Размер шрифта?  ПОЛЯ ? 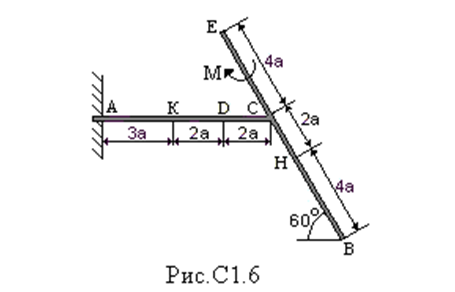  Решение: А) Выполняем действия в соответствии с порядком решения задач статики. Активная сила, а также момент пары сил М на рисунке уже показаны, действие распределенной нагрузки на участке СН заменяем равнодействующей силой, величина которой равна Q = q · 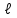 = 10·4а = 20кН, прикладывается сила Q в точке, делящей отрезок НB пополам. Объектом равновесия является конструкция, состоящая из двух прямолинейный стержней AС и ЕB, скрепленных в точке C.На балку связи наложены в точкеА, причем в точке А связью является жесткая заделка. Реакции и момент жесткой заделки в точке А неизвестны, поэтому при решении задач на рисунке показываются две взаимно перпендикулярные составляющие реакции ХА и УА, и момент МА . Покажем на рисунке реакции связей и выберем оси координат с началом в точке А.  В результате получилось, что на изучаемый объект действует произвольная плоская система сил, для равновесия которой должны выполняться три условия равновесия. Условия равновесия для балки запишем в виде уравнений проекций сил на оси координат Ах и Ау и уравнения моментов сил относительно точки А (выбор точки А для вычисления моментов удобен, так как моменты двух неизвестных по величине сил ХА и УА относительно точки А равны нулю и поэтому в такое уравнение моментов сил войдет лишь одна неизвестная величина МА. ) ∑Fix= 0; ∑Fiy= 0; ∑МА  = 0.Для вычисления моментов сил F и Q воспользуемся теоремой Вариньона, т.е. разложим эти силы на составляющие (  и  ), параллельные осям координат, и будем вычислять сумму моментов составляющих сил Qx, Q у относительно точки А.Шрифт  Проекции сил на оси координат равны: FY=F*sin15о ,FX=F*cos15 о, QY=Q*cos60 о, QX=Q*sin60 о Уравнения равновесия имею твид: Шрифт ∑Fix= 0 ХА  F∙cos15о – Q∙sin60о = 0; (1) ∑Fiy= 0 YA – F∙sin15о – Q∙cos60о = 0; (2) ∑MAi =0 МА – М –  –F·5a·cos75о= 0. (3) не проверял – на расчетной схеме нет ни одного размераПредставить правильно выполненную расчетную схему Далее не проверял Ошибки2: Для вычисления моментов сил F и Q воспользуемся теоремой Вариньона, т.е. разложим эти силы на составляющие ( и ), параллельные осям координат, и будем вычислять сумму моментов составляющих сил Qx, Q у относительно точки А. Проекции сил на оси координат равны: FY=F*sin15о ,FX=F*cos15 о, QY=Q*cos60 о, QX=Q*sin60 о Уравненияравновесияимеютвид: ∑Fix= 0 ХА F∙cos15о– Q∙sin60о = 0; (1) ∑Fiy= 0 YA – F∙sin15о –Q∙cos60о = 0; (2) ∑MAi =0 МА – М – –F·5a·cos75о= 0. (3)Выделенные размеры на рисунке не обозначены ВыразимМА из (3): 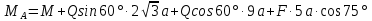 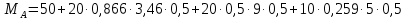 =131,4 кН мМА =131,4кН∙м Выразим ХА из (1): ХА= F∙cos15о + Q∙sin60о ХА =  =27кНХА =27кН Выразим YAиз (2): YA = F∙sin15о + Q∙cos60о YA= 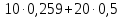 =12,6кНYA=12,6кН Ответ: МА =131,4 кН∙м, ХА =27кН, YA =12,6кН 3) определить, при каком значении угла αi, образуемого указанной в варианте задания сосредоточенной силой Fi с координатной осью, реакция в виде момента пары сил будет иметь минимальное по модулю значение, и для этого значения угла αiнайти все остальные реакции связей; Нам известно , что min момент при min плече силы F, у нас в таком случае угол а приравниваем к нолю. . Обозначим угол, под которым направлена силаF за 0. Тогда: Перепутаны разные величины: момент одной силы относительно точки и реакция всей конструкции при всех приложенных к ней воздействиях. Например, если α = - 15о, то МА станет меньше 120 кН м , а не 125, как ты утверждаешь.МА может стать еще меньше 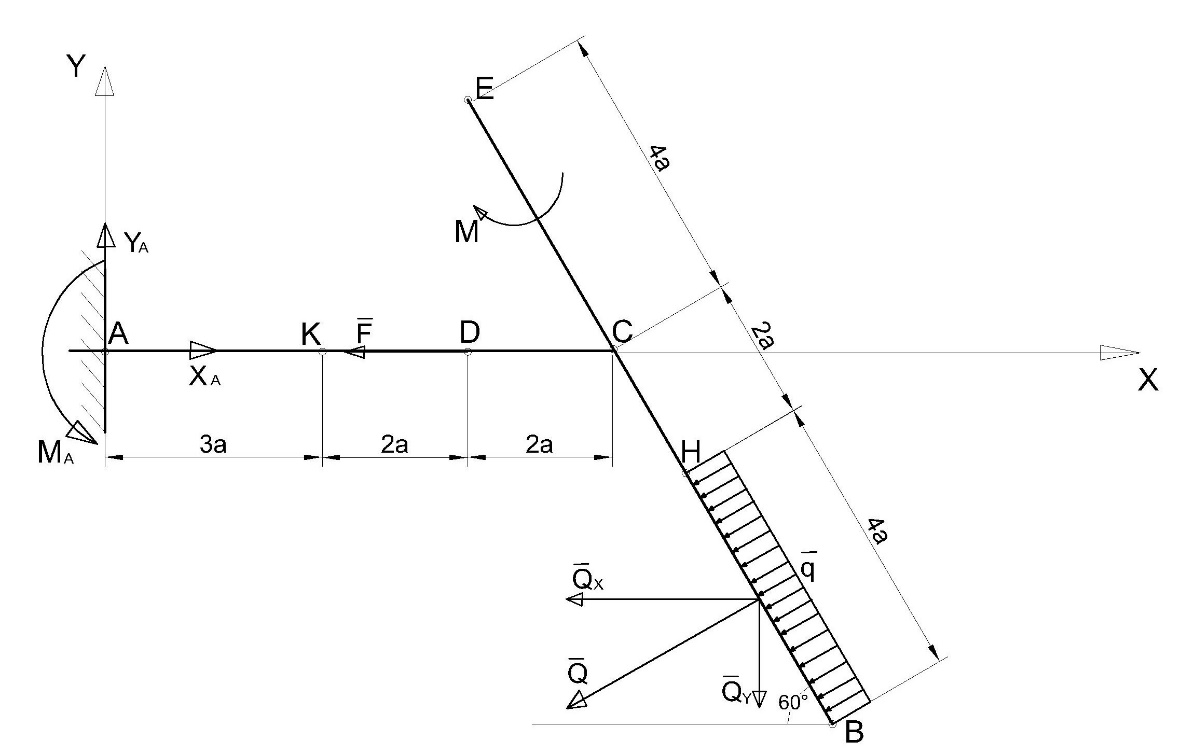 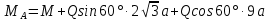 Найдем МА:  =125 кН мМА =125кН∙м Найдем ХА и УА при угле а=0о: ХА = F+ Q∙sin60о ХА =  =27,3кНХА =27,3кН YA =Q∙cos60о YA = 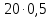 =10кНYA = 10кН Ответ: МА =125 кН∙м, ХА =27,3кН, YA = 10кН Исправить Пересчитать Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Институт архитектуры, строительства и дизайна  наименование института Кафедра механики и сопротивления материалов наименование кафедры РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА 1 По теоретической механике Задание С1 Определение реакций опор балки   шифр задания наименование задания Вариант № 66 Выполнил студент СУЗ-20-1 Д   .А. Маурершифр подпись Работа защищена Ю.В. Королев  И.О. Фамилия Иркутск 2021г. Задание С1 Определение реакций опор балки Конструкция, состоящая из двух прямолинейных стержней, жестко скрепленных между собой в точке С, расположена в вертикальной плоскости. На конструкцию действует пара сил с моментом М = 50 кН∙м, распределенная нагрузка интенсивности q = 10 кН/м, приложенная к участку HB вертикально вниз, и одна сосредоточенная сила F=10кН, приложенная к точке D под углом 15. При расчетах размер а принять равным 0,5 м. Для данной конструкции определить реакции связей конструкции; выяснить: − присутствует ли среди реакций связей изучаемой конструкции реакция в виде момента пары сил, и, если такая реакция имеется, то выполнить пункт 3, − если указанная реакция связи в виде момента пары сил отсутствует, то выяснить, в какой точке конструкции известно точное направление полной реакции связи в виде силы и для этой реакции выполнить пункт 4; определить, при каком значении угла αi, образуемого указанной в варианте задания сосредоточенной силой Fi с координатной осью, реакция в виде момента пары сил будет иметь минимальное по модулю значение, и для этого значения угла αiнайти все остальные реакции связей; для выбранной полной реакции связи в виде силы найти, при каком значении угла αi образуемого сосредоточенной силой Fiс указанной в варианте задании координатной осью данная реакция будет иметь минимальное по модулю значение, и для этого значения угла αiнайти все остальные реакции связей.  Решение: А) Выполняем действия в соответствии с порядком решения задач статики. Активная сила, а также момент пары сил М на рисунке уже показаны, действие распределенной нагрузки на участке СН заменяем равнодействующей силой, величина которой равна Q = q · 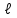= 10·4а = 20кН, прикладывается сила Q в точке, делящей отрезок НB пополам. Объектом равновесия является конструкция, состоящая из двух прямолинейный стержней AС и ЕB, скрепленных в точке C.На балку связи наложены в точке А, причем в точке А связью является жесткая заделка. Реакции и момент жесткой заделки в точке А неизвестны, поэтому при решении задач на рисунке показываются две взаимно перпендикулярные составляющие реакции ХА и УА , и момент МА . Покажем на рисунке реакции связей и выберем оси координат с началом в точке А. 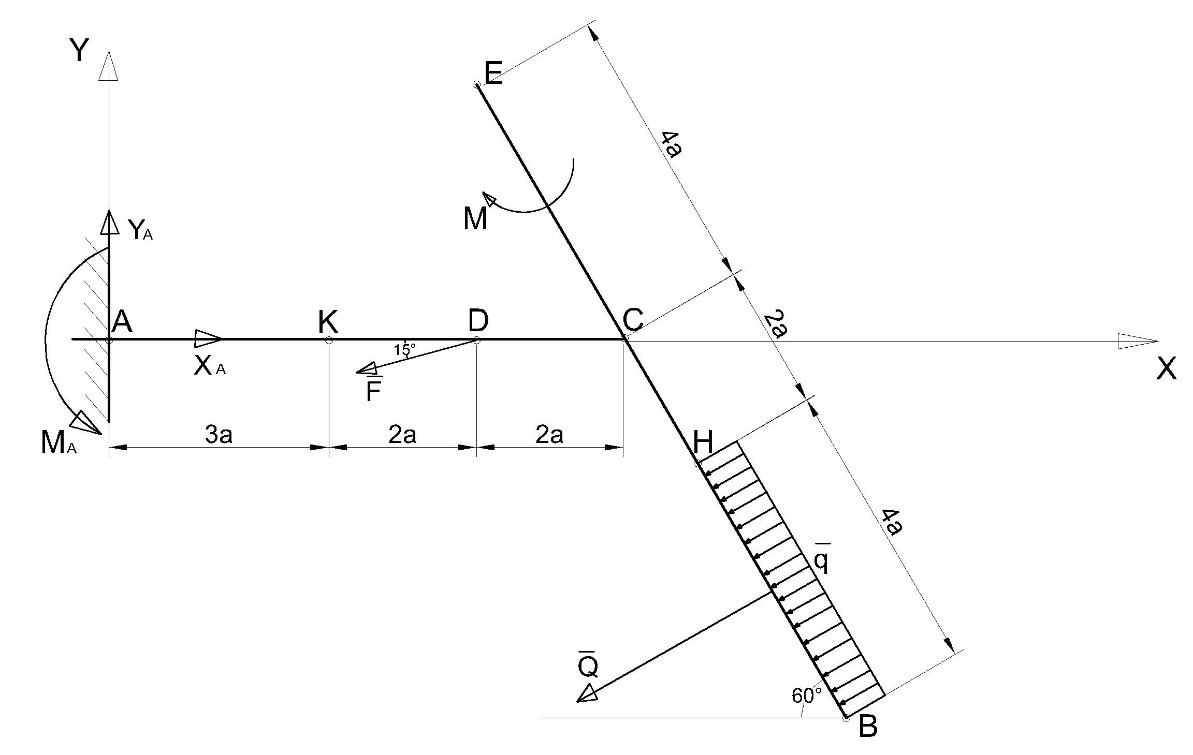 В результате получилось, что на изучаемый объект действует произвольная плоская система сил, для равновесия которой должны выполняться три условия равновесия. Условия равновесия для балки запишем в виде уравнений проекций сил на оси координат Ах и Ау и уравнения моментов сил относительно точки А (выбор точки А для вычисления моментов удобен, так как моменты двух неизвестных по величине сил ХА и УА относительно точки А равны нулю и поэтому в такое уравнение моментов сил войдет лишь одна неизвестная величина МА. ) ∑Fix= 0; ∑Fiy= 0; ∑МА = 0.Д 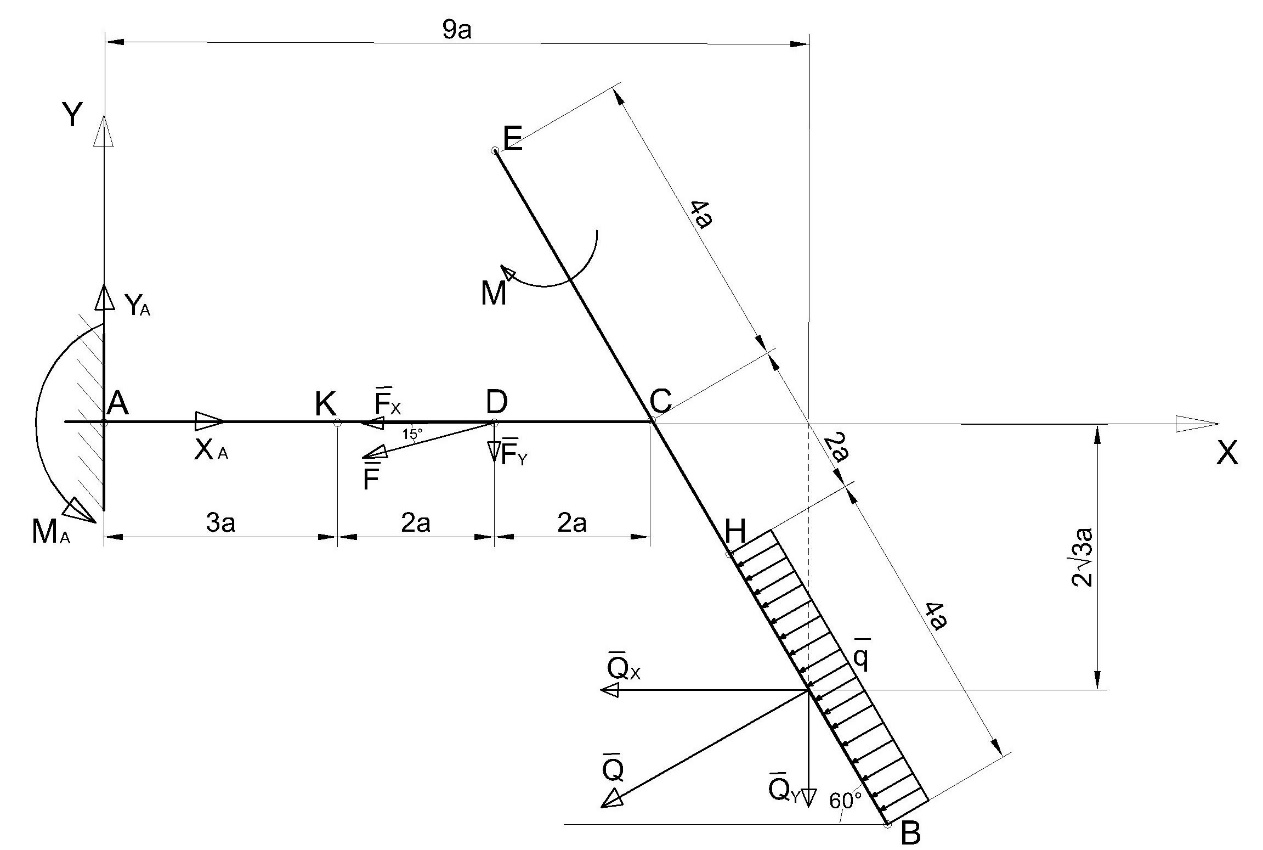 ля вычисления моментов сил F и Q воспользуемся теоремой Вариньона, т.е. разложим эти силы на составляющие ( и ), параллельные осям координат, и будем вычислять сумму моментов составляющих сил Qx, Q у относительно точки А.Проекции сил на оси координат равны: FY=F*sin15о , FX=F*cos15 о, QY=Q*cos60 о, QX=Q*sin60 о Уравнения равновесия имеют вид: ∑Fix= 0 ХА F∙cos15о – Q∙sin60о = 0; (1) ∑Fiy= 0 YA – F∙sin15о – Q∙cos60о = 0; (2) ∑MAi =0 МА – М – –F·5a·sin15о= 0. (3)Выразим МА из (3):   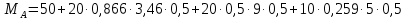=131,4 кН мМА =131,4 кН∙м Выразим ХА из (1): ХА = F∙cos15о + Q∙sin60о ХА = =27кНХА =27кН Выразим YA из (2): YA = F∙sin15о + Q∙cos60о YA = 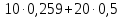=12,6кН YA =12,6кН Ответ: МА =131,4 кН∙м, ХА =27кН, YA =12,6кН 3) определить, при каком значении угла αi, образуемого указанной в варианте задания сосредоточенной силой Fi с координатной осью, реакция в виде момента пары сил будет иметь минимальное по модулю значение, и для этого значения угла αiнайти все остальные реакции связей; Угол под которым направлена сила обозначим за x:    (f)Из уравнения (f) видно, что искомая величина будет минимальна по модулю при x=270  (-90 ) :  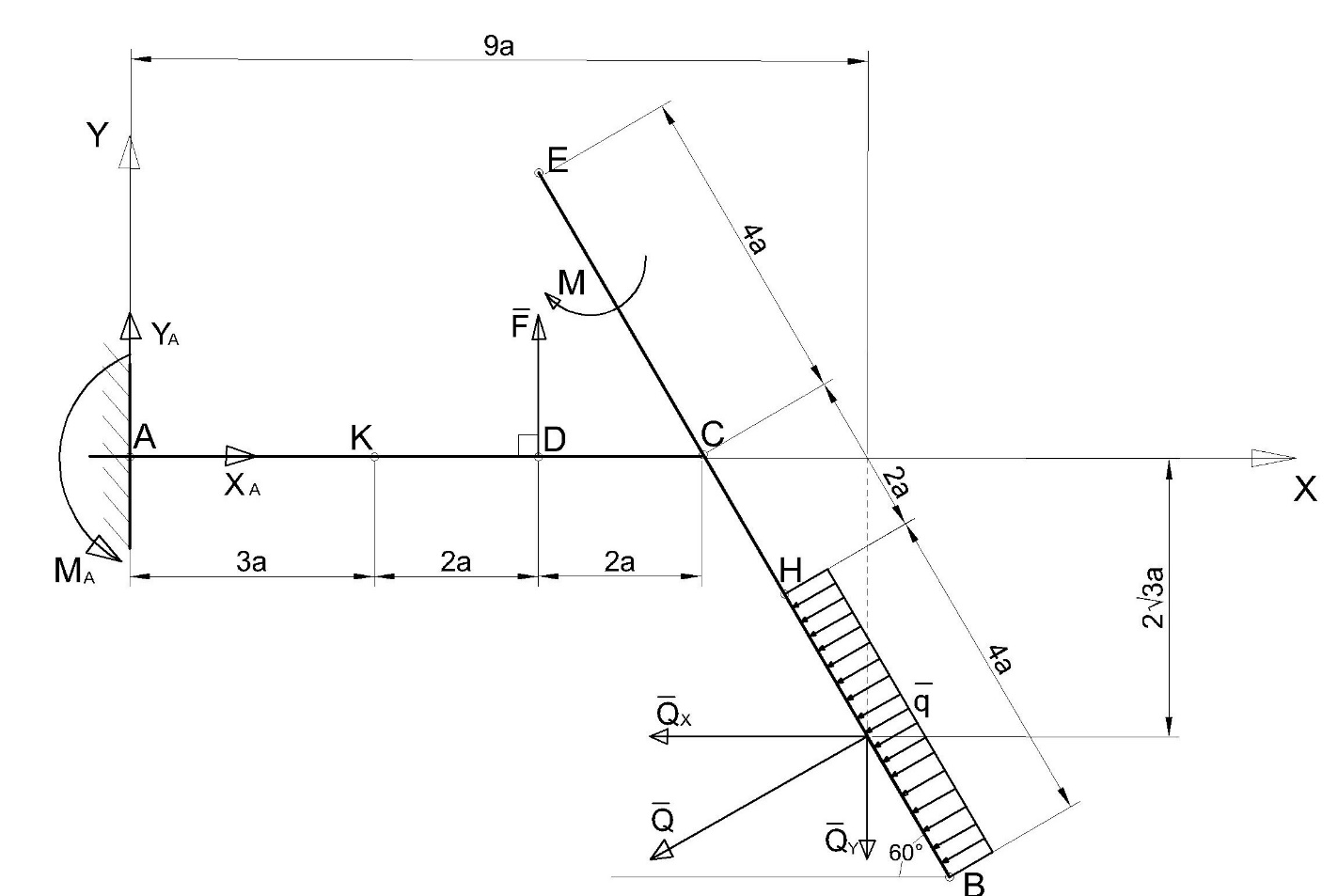 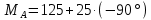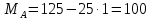кН мНайдем ХА и УА при угле а=270о: ХА = Q∙sin60о ХА =  = 17,3кНХА =17,3кН YA = Q∙cos60о - F YA = 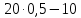 = 0YA = 0 Ответ: МА =100 кН∙м, ХА =17,3кН, YA = 0 |