Механика. Механика1 практическая работа 1. Тема Произвольная плоская система сил
 Скачать 117.26 Kb. Скачать 117.26 Kb.
|
Практическое задание 1Тема 1.2. Произвольная плоская система сил Задание 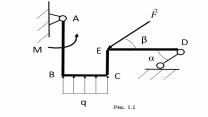 (рис. 1.1) (рис. 1.1) Жесткая рама (рис. 1.1) закреплена в точке А шарнирно, а в точке D прикреплена к невесомому стержню под углом α, равным 45 + 5П (град). На раму действует пара сил с моментом M, равным C + 1 (кН·м); внешняя сила F равная П + Г (кН), приложенная в точке А (если П = 0… 1), в другой точке В (если П = 2... 3), в точке С (если П = 4... 5), в точке Е (если П = 6... 7), в точке D (если П = 8… 9) под углом β к горизонту, равным 5 + 5Г (град) к горизонтали; распределенная нагрузка с интенсивностью Г (кН/м) вдоль колена АВ (длина которого 1 м) слева (если П = 0), вдоль колена ВС (длина которого 2 м) снизу (если П = 1... 2), вдоль колена АВ справа (если П = 3… 4), вдоль колена ВС сверху (если П = 5), вдоль колена СЕ (длина которого равна Г + 1 (м)) справа (если П = 6), вдоль колена ЕD (длина которого равна С + 1 (м)) сверху (если П = 7), вдоль колена СЕ слева (если П = 8), вдоль колена ЕD снизу (если П = 9). Определите реакции в точках А и D. Бланк выполнения задания 1
Жесткая рама (рис. 1.1) закреплена в точке А шарнирно, а в точке D прикреплена к невесомому стержню под углом α, равным 45 + 5*8 (град). На раму действует пара сил с моментом M, равным 6 + 1 (кН·м); внешняя сила F равная 8 + 8 (кН), приложенная в точке А (если П = 0… 1), в другой точке В (если П = 2... 3), в точке С (если П = 4... 5), в точке Е (если П = 6... 7), в точке D (если П = 8… 9) под углом β к горизонту, равным 5 + 5*8 (град) к горизонтали; распределенная нагрузка с интенсивностью 8 (кН/м) вдоль колена АВ (длина которого 1 м) слева (если П = 0), вдоль колена ВС (длина которого 2 м) снизу (если П = 1... 2), вдоль колена АВ справа (если П = 3… 4), вдоль колена ВС сверху (если П = 5), вдоль колена СЕ (длина которого равна 8 + 1 (м)) справа (если П = 6), вдоль колена ЕD (длина которого равна 6 + 1 (м)) сверху (если П = 7), вдоль колена СЕ слева (если П = 8), вдоль колена ЕD снизу (если П = 9). Определите реакции в точках А и D.      А        D     β    Е  М          q α          С В   Рис. 1.1 АВ / =1 (м) /ВС/ = 2 (м) /СЕ/ = 9 (м) /ЕD/ = 7 (м) α = 45 + 5*8 =85(град). M = 6 + 1 = 7(кН*м); F = 8 + 8=16 (кН), в точке D (если П = 8… 9) β = 5 + 5*8=40 (град); q = 8 (кН/м) вдоль колена СЕ слева (если П = 8) Определить реакции в точках А и D. Рассмотрим равновесие РАМЫ К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции. Активные (заданные) силы: F, Q, пара сил с моментом М, где Q- сосредоточенная сила, заменяющая действие распределенной вдоль отрезка ED нагрузки интенсивностью q. Величина Q=q*EC=8*9кН/м*M=72 кН Линия действия силы Силы реакции (неизвестные силы): Реакция Для полученной плоской произвольной системы сил можно составить три уравнения равновесия: Задача является статически определимой Поместим систему координат XY в точку А, ось ОX направим параплельно балке BC. За центр моментов всех сил выберем точку В. Составим уравнения равновесия: 1) ; 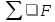 kx=0→Xa*cosβ=0 kx=0→Xa*cosβ=02) 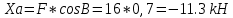 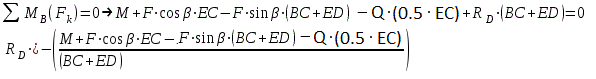 Rd- 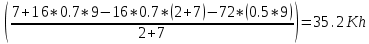 Ya-Q-F*cinB+Rd=0 Ya= Q-F*cinB-Rd=72-16*0.7+35.2=25.6kH Проверка В целях проверки взяли уравнение Σ Mb(Fk)=0→ M+F*cosB*EC-F*cinB*(BC+ED)-Q* (0.5*EC)+Rd(BC+ED)=0 7+16*0.7*9-16*0.7*(2+7)-72 (0.5*9)+35.2(2+7)=0 7+100.8-100.8-323.8+316.8=0 в результате подстановки в правую часть этого равенства данных задачи и найденных сил реакций получили нуль, задача решена - верно. Реакции найдены верно. найдем величину силы реакции неподвижного шарнира Ra= 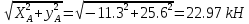 |
