Данилова С.Ю. работа. Федеральное государственное бюджетное образовательное учреждение высшего образования Ульяновский государственный педагогический университет им. И. Н. Ульянова
 Скачать 54.27 Kb. Скачать 54.27 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Ульяновский государственный педагогический университет им. И.Н.Ульянова» Факультет непрерывного образования и образовательных технологий Кафедра дошкольного и начального образования и методики преподавания общеобразовательных дисциплин Итоговая аттестационная работа Преемственность математического образования между начальной школой и 5-6 классами основной школы Выполнил: слушатель группы М-2 Данилова Светлана Юрьевна учитель математики МБОУ города Ульяновска «Гимназия №6 им. И.Н. Ульянова» Ульяновск 2022 ОглавлениеВведение 2 1. Математическое развитие детей 4 1.1 Задачи математического развития 4 1.2 Значение математики в развитии детей 6 2. Преемственность математического образования между начальной школой и 5-6 классами основной школы 10 2.1 Понятие «преемственности» 10 2.2. Проблемы преемственности в преподавании математики между начальной школой и 5 классом и пути их решения 12 2.3. Тестовые задания, предлагаемые для входного среза в 5 классе 17 Заключение. 25 Литература 29 ВведениеВедущими принципами ФГОС основного общего образования являются принципы преемственности и развития. Введение утвержденных на государственном уровне стандартов образования в значительной степени способствует обеспечению преемственности и перспективности повышения качества образования в целостной системе образования. ФГОС на каждой ступени общего образования содержит портрет выпускника соответствующей ступени. Портрет выпускника основной школы – это преемственная, углубленная и дополненная характеристика выпускника начальной ступени образования. Переход учащихся из начальной школы в основную, считается одной из наиболее сложных и значимых педагогических проблем, а период адаптации в 5 классе – одним из трудных периодов процесса обучения. Переходные периоды имеют ряд специфических проблем, которые требуют пристального внимания. Так как вопрос преемственности обучения – один из основополагающих вопросов педагогики, то при решении данного вопроса необходима продуманная система работы всех участников педагогического процесса: учащиеся, педагоги, администрация школы, специалисты психолого-педагогической службы. В настоящее время, когда школа вступила в процесс модернизации: внедрение новых технологий обучения, программ, методик, вопрос о преемственности стал наиболее актуальным и значимым. Преемственность обучения математике предполагает собой соблюдение правил последовательности, систематичности, взаимосвязанности и согласованности в методах и формах обучения, которые должны обеспечить безболезненный переход от одной системы обучения к другой. Что нужно при этом сделать, чтобы процесс адаптации ребенка к новым условиям и к новым требованиям прошел безболезненно? Как обеспечить успешность учащихся в последующей учебной деятельности? 1. Математическое развитие детей1.1 Задачи математического развитияМатематика всегда была неотъемлемой и существеннейшей составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и важной компонентой развития личности. Математика содержит в себе черты волевой деятельности, умозрительного рассуждения и стремления к эстетическому совершенству. Ее основные и взаимно противоположные элементы - логика и интуиция, анализ и конструкция, общность и конкретность. Ещё одной важнейшей причиной нужды человечества в математике является воспитание в человеке способности понимать смысл поставленной перед ним задачи, умение правильно, логично рассуждать, усвоить навыки алгоритмического мышления. Каждому надо научиться анализировать, отличать гипотезу от факта, критиковать, понимать смысл поставленной задачи, схематизировать, отчётливо выражать свои мысли и т. п., а с другой стороны - развить воображение и интуицию (пространственное представление, способность предвидеть результат и предугадать путь решения и т. д.). Иначе говоря, математика нужна для интеллектуального развития личности. Проблема обучения математике в современной жизни приобретает все большее значение. Это объясняется, прежде всего, бурным развитием математической науки и проникновением ее в различные области знаний. Повышение уровня творческой активности, проблемы автоматизации производства, моделирования на электронно-вычислительных машинах и многое другое предполагает наличие у специалистов большинства современных профессий достаточно развитого умения четко и последовательно анализировать изучаемые процессы. Поэтому обучение в детском саду направлено, прежде всего, на воспитание у детей привычки полноценной логической аргументации окружающего. Опыт обучения свидетельствует о том, что развитию логического детей в наибольшей мере способствует изучение математики. Для математического стиля мышления характерны четкость, краткость, расчлененность, точность и логичность мысли, умение пользоваться символикой. Доказано, что ознакомление детей с разными видами математической деятельности в процессе целенаправленного обучения ориентирует их на понимание связей и отношений. Формирование математических знаний и умений у детей должно осуществляться так, чтобы обучение давало не только непосредственный практический результат, но и широкий развивающий эффект. Под математическим развитием дошкольников, как правило, понимают качественные изменения в формах познавательной активности ребенка, которые происходят в результате формирования математических представлений и связанных с ними логических операций. Таким образом, из сказанного видно, что обучение математике в школе, в том числе в начальных классах, преследует достижение четырех взаимосвязанных целей: - общеобразовательных - овладение учащимися определенным объемом математических знаний, умений и навыков в соответствии с программой; - воспитательных – формирование важнейших моральных качеств, готовности к труду; - развивающих - развитие логических структур и математического стиля мышления; - практических - формирование умения применять математические знания в конкретных ситуациях, при решении практических задач. 1.2 Значение математики в развитии детейМатематика - это фундаментальная наука, методы которой, активно применяются во многих естественных дисциплинах, таких как физика, химия и даже биология. Сама по себе, эта область знаний оперирует абстрактными отношениями и взаимосвязями, то есть такими сущностями, которые сами по себе не являются чем-то вещественным. Но, тем не менее, стоит только математике вступить в область любой науки о мире, она сразу воплощается в описание, моделирование и предсказание вполне себе конкретных и реальных природных процессов. Математика развивает умственные способности. Она позволяет развить важные умственные качества. Это аналитические, дедуктивные (способность к обобщению), критические, прогностические (умение прогнозировать, мыслить на несколько шагов вперед) способности. Также эта дисциплина улучшает возможности абстрактного мышления (ведь это абстрактная наука), способность концентрироваться, тренирует память и усиливает быстроту мышления. Если говорить более подробно и оперировать конкретными навыками, то математика поможет ребенку развить следующие интеллектуальные способности: Умение обобщать. Рассматривать частное событие в качестве проявления общего порядка. Умение находить роль частного в общем. Способность к анализу сложных жизненных ситуаций, возможность принимать правильное решение проблем и определяться в условиях трудного выбора. Умение находить закономерности. Умение логически мыслить и рассуждать, грамотно и четко формулировать мысли, делать верные логические выводы. Способность быстро соображать и принимать решения. Навык планирования наперед, способность удерживать в голове несколько последовательных шагов. Навыки концептуального и абстрактного мышления: умение последовательно и логично выстраивать сложные концепции или операции и удерживать их в уме. Математическому мышлению свойственны те качества, которые присущи научному мышлению. В исследованиях Ю. Н. Колягина, это: 1) Гибкость мышления - способность к целесообразному варьированию способов действия; легкость перестройки системы знаний, умений и навыков при изменении условий действия; легкость перехода от одного способа действия к другому, умение выходить за границы привычного способа действия. 2) Активность мышления - постоянство усилий, направленных на решение некоторой проблемы, желание обязательно решить эту проблему, изучить различные подходы к ее решению, исследовать различные варианты постановки этой проблемы в зависимости от изменяющихся условий и т. д. 3) Организованность памяти. В зависимости от содержания запоминаемого материала и от деятельности человека в процессе запоминания память делят на образную (двигательную, зрительную, слуховую), эмоциональную и словесно-логическую. В зависимости от целей деятельности различают память непроизвольную и избирательную. В зависимости от времени хранения информации в памяти различают память кратковременную (оперативную) и долговременную. 4) Широта мышления - способность к формированию обобщенных способов действий, имеющих широкий диапазон переноса и применения к частным, нетипичным случаям. Это качество мышления часто проявляется в готовности школьников принять во внимание новые для него факты в процессе деятельности в известной ситуации. 5) Глубина мышления - способность глубокого понимания каждого из изучаемых математических фактов в их взаимосвязи с другими фактами. 6) Критичность мышления - умение оценить правильность выбранных путей решения проблемы и получаемые при этом результаты с точки зрения их достоверности, значимости и т. п. В процессе обучения математике воспитанию этого качества у учащихся способствует постоянное обращение к различного вида проверкам, грубым прикидкам найденного результата, а также к проверке умозаключений, сделанных с помощью индукции, аналогии и интуиции. Математика развивает творческие способности. К творческим способностям, с точки зрения Ю. М. Колягина, относятся прежде всего: - способность к правильному и быстрому восприятию, способность к пространственному воображению; - способность к быстрому сосредоточению и переключению внимания с сохранением его устойчивости и интенсивности на любых избранных объектах; - наличие хорошей избирательной памяти, способность репродуцировать ведущие знания и опыт; - способность к сильному творческому воображению; - способность оценивать ситуацию сразу с различных точек зрения, способность видеть больше того, что есть и что очевидно; - способность проникать в сущность основных взаимосвязей, скрытых в данной проблеме, перед тем как приступить к ее решению; - устойчивую потребность в познании нового; - образность, точность и сжатость речи, способность необычно отвечать на специфические вопросы; - способность создавать наглядно-действенные и наглядно-образные модели тех или иных ситуаций; - способность мыслить отвлеченно, схватывая главную суть закономерности изучаемого процесса или характеристические свойства той или иной ситуации. Важно отметить, что к числу качеств, присущих творческой личности, справедливо относят и такие качества, как: глубокие и широкие знания в области своей деятельности; всестороннюю (или узконаправленную) любознательность; мечтательность, склонность к фантазии; независимость суждений; находчивость, способность к импровизации; склонность к риску и т. д. Нетрудно видеть, что в перечисленных качествах творческой личности проявляется высокий уровень развития самых разнообразных компонентов, присущих математическому мышлению. Таким образом, математика необходима для развития ребенка. Она задает стандарты правильного, рационального мышления на всю жизнь вперед. Дает огромный толчок для умственного развития. Этот школьный предмет способен намного поднять умственный уровень подрастающего индивида и послужить хорошим подспорьем для интеллектуального развития впоследствии, уже в зрелом возрасте. Он организует, упорядочивает и оптимизирует мышление, тренирует, такие умственные качества, которые формируют каркас и скелет всего мышления. 2. Преемственность математического образования между начальной школой и 5-6 классами основной школы2.1 Понятие «преемственности»Преемственность в обучении – установление необходимой связи и правильного соотношения между частями учебного предмета на разных ступенях его изучения; понятие преемственности характеризует также требования, предъявляемые к знаниям и умениям учащихся на каждом этапе обучения, формам, методам и приёмам объяснения нового материала и ко всей последующей работе по его усвоению. Преемственность в изложении учебного материала и выборе способа деятельности по овладению этим содержанием происходит с учетом следующих факторов: содержания и логики математической науки и закономерностей процесса усвоения знаний. Преемственность должна осуществляться и между видами деятельности учащихся при усвоении учебного материала. Учащиеся должны выступать не как объект обучения, а становиться субъектами учебной деятельности. В новых стандартах образования нашли отражение инновационные научные идеи, которые активно разрабатывались педагогами, психологами и методистами: системно - деятельностный подход и личностно-ориентированное обучение, дифференциация, гуманизация и гуманитаризация образования, теория учебной деятельности, формирование общеучебных умений, взаимосвязь обучения, воспитания и развития учащихся и т.д. В начальных классах в соответствии со стандартом, основной задачей изучения математики является "формирование представлений о натуральном числе, выработка прочных навыков вычислений с натуральными числами и нулем, обучение применению натуральных чисел при решении практических задач". Поэтому, преемственные связи находят свое выражение в том, что курс математики 5 класса так же как и курс математики начальной школы сориентирован на отработку частных вопросов. Это оказывает влияние на способы реализации преемственности между ступенями образования, которые находят отражение и при изучении натуральных чисел и дробей. В качестве основных способов реализации преемственности выступают: Повторение, пронизывающее весь курс математики 5-6 классов. Это находит свое выражение как в специальном разделе "Натуральные числа", так и при изучении новых вопросов, где предлагаются упражнения для повторения ранее изученного материала в большинстве случаев с натуральными числами; При введении нового материала используются объяснительные тексты, в которых авторы учебников взаимосвязь с вопросами, ранее изученными на начальной ступени, выражают формулировками типа: "Вы уже умеете...", "В предыдущих классах вы изучали..." и т.д. Тем не менее эти фразы носят формальный характер, так как при дальнейшем изложении объяснительного текста эти знания и умения детей не используются, а все "разъясняется" с самого начала. При этом деятельность учащихся носит репродуктивный характер, отражает образец, данный в объяснительном тексте или учителем. Эти способы реализации преемственности носят внешний, формальный характер и не формируют в сознании учащихся необходимую понятийную взаимосвязь, так как она не находит достаточного выражения в заданиях, которые являются основным средством организации учебной деятельности учащихся, а отражена только в объяснительных текстах учебника. Если же рассмотреть преемственность между начальной и основной ступенями в случае, когда обучение в начальных классах ведется по развивающим программам, то разрыв между ними еще значительнее, так как работа по развитию учебной деятельности и мышления учащихся, начатая в начальных классах, не получает должного продолжения ни в одном из рассматриваемых учебников. 2.2. Проблемы преемственности в преподавании математики между начальной школой и 5 классом и пути их решенияПроблемы преемственности в преподавании математики между начальной школой и 5 классом можно поделить на три группы: организационно-психологические; общеучебные умения и навыки; специальные математические знания, умения и навыки. Организационно-психологические проблемы. 1. Недостаточная наполняемость урока материалом, неоправданно медленный темп урока, отсутствие материалов для «сильного» ученика, перенос основной тяжести усвоения курса на домашнюю работу. Возможности разрешения: уменьшение доли фронтальных бесед и других малоэффективных методов работы на уроке, использование печатных дидактических материалов, уменьшение пауз в работе детей. 2. Недостаточно организованное и четкое начало урока, окончание урока, выделение дополнительного (сверх отведенных 45 мин.) времени на выполнение письменных проверочных работ, из-за чего дети не приучаются быстро включаться в работу, эффективно и быстро работать. Возможности разрешения: приучать начинать работу на уроке по звонку, быстро включаться в работу, не давать отдельным детям дополнительного времени на выполнение контрольных и проверочных работ, заканчивать урок также со звонком с урока. 3. Стойкая привычка у детей к неумеренной помощи родителей при выполнении домашних заданий, творческих работ. Возможности разрешения: разъяснения родителям наносимого ущерба интеллектуальному развитию их ребенка, включение в уроки заданий, контролирующих степень самостоятельности при выполнении домашних заданий. 4. Бедность и однообразие используемых материалов обучения, несоответствие методического багажа учителя реальным учебным возможностям детей. Возможности разрешения: распространение опыта успешного обучения детей в современных условиях (школьным методическим объединениям учителей начальных классов и математики полезно знакомиться с лучшим опытом). 5. Пассивность большинства учащихся в процессе обучения. Возможности разрешения: использование форм и методов организации занятий, требующих от каждого ученика активного и осознанного участия, в том числе парной и групповой работы. 6. Несформированность у учащихся представления об отличном устном ответе, ответе у доски на уроке математике. Возможности разрешения: учителям математики совместно с учителями начальной школы определиться в требованиях к ответу ученика и постепенно разъяснять детям эти требования, учитывать их, оценивая ответы на уроке. 7. Привычка у детей получать отметки за любое (самое малое) действие, в т.ч. за краткие или односложные, невразумительные ответы. Возможности разрешения: добиваться от детей развернутых, полных ответов, четкой и грамотной речи, не допускать выставления необоснованно высоких оценок за неполные ответы. 8. Обедненная речь учителя, отсутствие динамики в использовании лексики от 1 к 4 классам. Возможности разрешения: полезно создание и внедрение учителями математики совместно с учителями начальной школы словаря-программы постепенного ознакомления детей с «взрослой» лексикой, проведение отдельных уроков в начальной школе вместе с учителем средних классов. 9. Создание у детей учителем и родителями в конце 4 класса «психологического барьера» - настороженного ожидания трудностей учения в 5 классе. Возможности разрешения: знакомство родителей и детей со своими будущими учителями уже в 4 классе, проведение математических праздников, олимпиад, соревнований, отдельных уроков, родительских собраний совместно с учителем 5 класса. Общеучебные умения и навыки. 1. Недостаточная техника чтения, большие проблемы в понимании текста учащимися из-за обедненного лексического запаса у части детей, неумение делить текст на смысловые части и анализировать его. Возможности разрешения: постоянно предлагать учащимся задания на проверку знания и понимания смысла математических терминов, вести словарики терминов, читать вслух и анализировать условия задач, рекомендовать и родителям проводить такую работу с детьми при выполнении заданий по математике. 2. Недостаточная скорость письма, нечеткий почерк у значительной части детей. Возможности разрешения: рекомендовать упражнения для развития мышц кисти руки, подходящую ручку, продолжать следить за правильностью написания букв и цифр, за верным положением ручки. 3. Неустойчивость внимания, слабо развитая оперативная память у многих детей. Возможности разрешения: на уроках предлагать цепочные вычисления, дома – специальные упражнения на тренировку внимания и памяти. 4. Недостаточная тренированность долговременной механической памяти. Возможности разрешения: практиковать письменный опрос правил, предлагать для запоминания не только стихотворные, но и прозаические тексты. 5. Отсутствие у учащихся умения и привычки обращаться к энциклопедиям, справочникам, словарям, научно-популярной и дополнительной литературе. Возможности разрешения: рекомендовать иметь в классе справочные издания, предлагать учащимся задания по работе со справочниками и словарями, поручать готовить сообщения, рассказы, сочинения по материалам дополнительной литературы. Специальные математические знания, умения и навыки. 1. Недостаточные умения устных вычислений (все арифметические действия в пределах до ста учащиеся должны выполнять устно). Возможности разрешения: постоянное подкрепление знаний таблиц сложения и умножения, систематическое проведение содержательного и напряженного устного счета. 2. Ошибки в письменном делении многозначных чисел и письменном умножении многозначных чисел. Возможности разрешения: регулярное повторение всех этапов алгоритма выполнения деления и умножения, систематическое включение в устную работу заданий на табличное умножение и деление, сложение и вычитание. 3. Слабое знание правил порядка действий (в том числе и в выражениях со скобками). Возможности разрешения: после записи вычислительных примеров начинать с выделения отдельных «блоков», из которых он состоит, обращать внимание на «сильные» и «слабые» знаки арифметических действий, а затем расставлять номера действий. 4. Недостаточные умения решать текстовые задачи (даже в одно - два действия). Возможности разрешения: предлагать сначала представить себе ситуацию, о которой идет речь в задаче, изобразить её на рисунке или схеме; при обсуждении решения – вопросы: как догадались, что первое действие именно такое? 5. Недостаточное развитие графических умений. Возможности разрешения: регулярное выполнение чертежей как на бумаге в клетку, так и на нелинованной бумаге, построение фигур по командам. 6. Формальные представления об уравнении, его корне, способах проверки правильности решения уравнения. Возможности разрешения: большее внимание уделять первым этапам формирования понятия переменной, верного и неверного равенства, нахождение значения выражения с переменной. 7. Недостаточно грамотная математическая речь учащихся. Возможности разрешения: учителю чаще давать образцы чтения выражений, равенств, уравнений и неравенств, склонять числительные, тренировать школьников в верном чтении математических выражений, использовании названий натуральных чисел и дробей в косвенных падежах. Итак, для успешного решения проблемы преемственности на современном этапе необходимо: полностью согласовать требования к математической подготовке учащихся, сформулированные в программах начальной и основной школы; согласовать методы обучения, обеспечивающие достаточную подготовку учащихся младших классов к восприятию обобщенных фактов, правил, законов, адаптацию школьников к дедуктивному методу изложения; строить обучение математике так, чтобы достижение учащимися обязательных результатов обучения было безусловным требованием и непременно контролировалось; выявить опорные умения для смежных дисциплин; сгладить переход от одного учителя ко многим учителям-предметникам; создать оптимальные условия для реализации системы средств обучения, разработать комплекс учебных пособий. установить тесную связь в методах работы с учащимися между учителями 4-х и 5-х классов. 2.3. Тестовые задания, предлагаемые для входного среза в 5 классеИнструкция учащемуся В тесте 20 заданий, проверяющих твою подготовку по математике. К некоторым заданиям даны 4 ответа для выбора, они обозначены буквами А, Б, В, Г. Только один из них верный. Внимательно прочитайте каждое задание. Выполните его. Обведите кружком букву, которая соответствует правильному ответу. Пример 1. Сколько минут в 1 часе? А. 100. Б. 60. В. 600. Г. 3600. В 1 часе содержится 60 минут, поэтому обведена буква Б. Если к заданию не даны ответы для выбора, то свой ответ запишите над чертой. Пример 2. Сколько копеек содержится в 1 рубле? Ответ: 100. В одном рубле содержится 100 копеек, поэтому после слова «Ответ» вписано число 100. Задание считается выполненным верно, если обведена кружком буква, соответствующая правильному ответу, или записан верный ответ. При этом не требуется ни подробная запись решения, ни объяснение выбранного ответа. Постарайся выполнить верно, как можно больше заданий. Вычисления столбиком делай в любом свободном месте этого листа. ВАРИАНТ 1 Запишите цифрами число (№№ 1,2): 1. Три тысячи сто два. Ответ: __________________. 2. Четырнадцать тысяч пятьсот двадцать. Ответ: __________________. Выполните действия (№№ 3 – 8): 3. 46305 + 2738. Ответ: __________________. 4. 7269 – 3523 Ответ: __________________. 5. Ответ: _________________. 6. : 27 Ответ: __________________. 7. Ответ: __________________. 8. 6300 : 9 А. 7. Б. 70. В. 700. Г. 7000. 9. Выберите правильный порядок действий: 3 1 2 4 3 2 1 4 А. 200 – (12 + 498 : 6) · 2. Б. 200 – (12 + 498 : 6) · 2. 4 1 2 3 4 2 1 3 В. 200 – (12 + 498 : 6) · 2. Г. 200 – (12 + 498 : 6) · 2. Сравните числа (поставьте между ними знак <, >) (№№ 10 – 12) 10. 295 ______925. 11. 1024______1824. 12. 1648______959. 13. Ширина прямоугольника 80 см, а длина на 10 см больше, чем ширина. Найдите длину прямоугольника А. 800см. Б. 8см. В. 70см. Г. 90см. 14. В спортивной секции занимается 16 мальчиков и несколько девочек. Девочек – в 4 раза меньше, чем мальчиков. Сколько девочек занимается в спортивной секции? А. 4. Б. 12. В. 20. Г. 64. 15. Турист прошел в первый день 18 км, а во второй день на 6 км меньше. Сколько километров прошел турист за два дня? Ответ: __________________. 16. Дочери 6 лет, а маме в 5 раз больше. На сколько лет мама старше дочери? Ответ: __________________. 17. В классе 30 учащихся. Третья часть всех учащихся поет в хоре. Сколько учащихся поет в хоре? Ответ: __________________. 18. Купили три пакета молока по 3р. 50к. за пакет. Сколько сдачи должны получить с 15р.? Ответ: __________________. 19. Стороны прямоугольника равны 13 см и 9 см. Найдите его периметр? Ответ: __________________. 20. Стороны прямоугольника 20 см и 14 см. Найдите его площадь? Ответ: __________________. ВАРИАНТ 2 Запишите цифрами число (№№ 1,2): 1. Четыре тысячи двести три. Ответ: __________________. 2. Пятнадцать тысяч шестьсот десять. Ответ :__________________. Выполните действия (№№ 3 – 8): 3. 16847 + 5308. Ответ: __________________. 4. 4357 – 3129. Ответ: __________________. 5. . Ответ: __________________. 6. 276 : 23. Ответ: __________________. 7. Ответ :__________________. 8. А. 120 000. Б. 12 000. В. 1200. Г. 120. 9. Выберите правильный порядок действий: 1 2 3 4 2 1 4 3 А. 240 – 36 + 51 : 3 · 2. Б. 240 – 36 + 51 : 3 · 2. 3 4 2 1 3 4 1 2 В. 240 – 36 + 51 : 3 · 2. Г. 240 – 36 + 51 : 3 · 2. Сравните числа (поставьте между ними знак <, >) (№№ 10 – 12) 10. 327 ______723. 11. 1937______1037. 12. 1856______941. 13.Длина прямоугольника равна 60 см, а ширина на 20 см меньше, чем длина. Найдите ширину прямоугольника. А. 40см. Б. 3см. В. 80см. Г. 1200см. 14. Общая тетрадь стоит 1р. 50к., а книга в 3 раза дороже. Сколько стоит книга? А. 50к. Б. 4р. 50к. В. 1р. 53к. Г. 1р. 47к. 15. Мальчик прочитал в первый день 18 страниц, а во второй – на 6 страниц больше. Сколько страниц прочитал мальчик за два дня? Ответ: __________________. 16. В мастерской было 420 м материи. Сколько материи осталось в мастерской после того, как в каждый из пяти дней израсходовали по 60 м материи? Ответ: __________________. 17. Туристы прошли 12 км. Они прошли только третью часть всего маршрута. Определите длину маршрута. Ответ: __________________. 18. Расстояние между двумя городами поезд прошел со скоростью 80 км в час за 3 ч. Определите длину маршрута. Ответ: __________________. 19. Стороны прямоугольника равны 30 см и 12 см. Найдите его периметр? Ответ: __________________. 20. Стороны прямоугольника 15 см и 8 см. Найдите его площадь? Ответ: __________________. 2.4. Математические игры Одно из эффективных средств развития интереса к учебному предмету, наряду с другими методами и приемами, используемыми на уроках, — дидактическая игра. Еще К.Д. Ушинский советовал включать элементы занимательности, игровые моменты в учебный труд учащихся для того, чтобы процесс познания был более продуктивным. Игра занимает значительное место в первые годы обучения детей в школе. В начале учащихся интересует только сама форма игры, а затем уже и тот материал, без которого нельзя участвовать в игре. Использование потребностей детей к игре порождает особый вид игр – дидактической игры и особую форму занятий – игровую форму. Во внеклассные занятия по математике в малокомплектной начальной школе игра привносит дух любознательности, интереса, познания и открытия, а сами занятия делают занимательными, доступными детям. Использование дидактических игр во внеклассной работе в малокомплектной начальной школе не только способствует лучшему усвоению программного материала по математике, но и развитию логического мышления, речи, развитию наблюдательности, внимания и интереса к предмету. Следует различать игру, дидактическую игру и игровую форму занятий. Под дидактической игрой понимается игра, используемая в целях обучения ивоспитания. Под игровым занятием понимается занятие, пронизанное элементами игры или содержащее игровую ситуацию. Дидактическая игра отличается тем, что участие в ней обязательно и определяется требованием учителя. Игровое занятие может включать одну или несколько связанных между собой дидактических игр. Игровое занятие тоже является обязательным. Мотив деятельности может определяться для ученика и игровыми моментами, и сюжетом, и правилами. Дидактические игры и игровые занятия, разработанные с учетом особенностей игр подростков,особенностей предмета и конкретных условий отличаются эмоциональностью, у школьников они вызываютумственное напряжение, обостряют интеллектуальные процессы. В ходе игры учащиеся незаметно для себя выполняют различные упражнения, где им самим приходится сравнивать, выполнять арифметические действия, тренироваться в устном счете, решать задачи. Игра ставит учащихся в условия поиска, пробуждает интерес к победе, следовательно, дети стремятся быть быстрыми, находчивыми, четко выполнять задания, соблюдать правила игры. В играх, особенно коллективных, формируются и нравственные качества ребенка. В ходе игры дети учатся оказывать помощь товарищам, считаться с мнением и интересами других, сдерживать свои желания. У детей развивается чувство ответственности, коллективизма, воспитывается дисциплина, воля, характер. Активизировать деятельность учащихся по овладению математическими знаниями можно путем умелого применения занимательных заданий. Занимательность характеризуется следующими показателями: новизна; необычность, неожиданность; несоответствие прежним представлениям. Занимательная задача – это такая задача, которая вызывает непроизвольный интерес, являющийся следствием необычности сюжета, непривычной формы ее подачи. Решение таких задач вырабатывает у учащихся внутренний положительный отклик, развивает их любознательность. Дидактическая игра, игровое занятие должны разрабатываться так, чтобы к учащимся были предъявлены определённые требования в отношении знаний. Игра должна носить познавательный характер. Для младших учащихся интересны игры с включением ролей, сюжета соревновательного характера. Правила и организация игр должны разрабатываться с учетом индивидуальных особенностейучащихся. Для каждой категории учащихся надо создать условия для проявления самостоятельности, инициативы, смекалки. Каждый ученик должен испытать радость успеха, состояние уверенности в себя, в свои возможности. Дидактические игры и игровые ситуации должны быть разнообразными и разрабатываться с учетомособенностей математики. Все игры должны составлять систему, в которой необходимы обучающие и контролирующие игры (по назначению), групповые и индивидуальные (по массовости), подвижные и тихие (пореакции), «скоростные» и «качественные» (по темпу), одиночные и универсальные. Игра «Какое число заложено в машину» 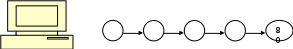 ·3 :2 +30 -12 Подвижная игра «Найди свое место» Для игры необходимо подготовить два комплекта карточек (в зависимости от числа играющих) с примерами. Дается команда собраться и построиться в шеренгу по порядку номеров. Побеждает команда, сумевшая построиться первой. Прочитайте и отгадайте загадку Для этого надо использовать только те числа, которые входят в таблицу умножения.
Ответ: В воле она живёт, Нет клюва, а клюёт. (Рыба) «Кто ушел?» Ученики строятся в круг. Водящий встает в центр круга, запоминает, какие цифры на карточках в руках у детей (только четные; только нечетные; по возрастанию; по убыванию и т.д.) закрывает глаза. Учитель дотрагивается до одного из играющих, стоящих в круге, и он тихо выходит из зала. Учитель спрашивает у водящего: «Отгадай, кто ушел?» (какой цифры не хватает). Если водящий отгадал, то он встает в круг и выбирает другого водящего. Если не отгадал, то снова закрывает глаза, а выходивший из зала занимает своё прежнее место в кругу. Водящий, открыв глаза, должен назвать его. Заключение.Итак, преемственность между уровнями начального общего и основного общего образования – это двухсторонний процесс. С одной стороны − начальная ступень, которая формирует те знания, умения и навыки, которые необходимы для дальнейшего обучения в основной школе. С другой стороны – основная школа, которая развивает (а не игнорирует) накопленный в начальной школе потенциал. Некоторые вопросы преемственности можно решить, если учителя начальной и основной школы будут работать в тесном контакте – это и взаимопосещение уроков, совместные заседания предметных кафедр, в нашей гимназии также практикуется, что учителя, которые возьмут класс в 5 классе, ведут внеурочную деятельность связанную с предметом, так можно познакомиться с учащимися, изучить их особенности, получить представление об уровне знаний. Чтобы детям лучше было адаптироваться к новым для них условиям, учителю необходимо начать процесс обучения с тех методов и приемов, которые использовал учитель начальных классов. Ведь если посмотреть на содержание учебного материала в 5 классе, то он в большей степени является обобщением тех знаний, с которыми дети пришли из начальной школы. Например, дети на начальной ступени обучения знакомятся с числами, но в дальнейшем их сведения о числах расширяются: знакомятся с новыми классами, получают сведения об обыкновенных и десятичных дробях, а в последствие, в 6 классе, изучают отрицательные числа. При этом, те ЗУН, которыми учащиеся владели на начальной ступени обучения, находят свое дальнейшее применение при изучении новых тем. Чтобы процесс обучения был успешным, важным условием является создание благоприятного психологического климата. Использование педагогической технологии – создание ситуации успеха, способствует созданию комфортной атмосферы на уроке. Учитель должен дать возможность каждому ребенку проявить свои способности. К.Д.Ушинский считал, что только успех поддерживает интерес к учению, а интерес проявляется только тогда, когда есть вдохновение, которое рождается от успеха в овладении знаниями. Ученый, психотерапевт и педагог У.Глассер считал, что успех должен быть доступен каждому ребенку. Но здесь возникает вопрос: «Как создать ситуацию успеха»? Учителю необходимо, как можно быстрее запомнить имена детей. Американский психотерапевт Э.Берн считает, что «Ничто не ласкает человеческий слух, как называние его по имени». Выражение подбадривания, похвалы: «Молодец», «У тебя сегодня все получилось…», «Твой ответ сегодня такой же яркий, как солнышко» и т.д. Использование игровых технологий с применением ИКТ способствует созданию ситуации успеха. В.А. Сухомлинский считал: «Без игры не может быть полноценного умственного развития. Игра – это искра, зажигающая огонек пытливости и любознательности». Игровые технологии направлены на развитие общеучебных навыков, формирование и развитие коммуникативной компетенции (дети учатся слушать и слышать собеседника, вступать с ним в диалог). Применение игровых моментов на уроке делает урок более интересным, облегчает преодоление трудностей у детей. Элементы игры я использую на любом этапе урока. Например, решив ребус или анаграмму, дети формулируют тему урока. При устном счете использую математические лабиринты, кроссворды, ребусы и головоломки. Использование приемов ТРКМ, таких как «Корзина идей», «Ромашка Блума», «Пазл», также направлены на создание ситуации успеха на уроке. Эти приемы позволяют каждому ребенку проявить свои способности и реализовать их в деятельности. Особенно детям нравится прием «Пазл», когда они самостоятельно в программе Jigsaw Puzzle2 создают «Пазл» по изученной теме, а затем показывают их в классе. На своих уроках я использую следующие виды совместной деятельности: Взаимоконтроль и взаимоопрос (задают друг другу вопросы по изученной теме, сравнивают свой вариант ответа с ответами других учеников). Взаимная оценка (анализ работы товарища, по критериям, которые записаны учителем на доске) Выполнение творческих заданий и обсуждение проблем. Процесс оценивания знаний. При выставлении отметки, детям необходимо разъяснять критерии оценивания, если у ребенка имеются пробелы в знаниях, то ему необходимо разъяснить над чем ему следует поработать. На мой взгляд, оценочная деятельность должна носить стимулирующий и поддерживающий характер. Домашнее задание необходимо комментировать и давать инструкцию по его выполнению. Соблюдение принципа преемственности и систематичности в обучении математике - залог усвоения и получения новых знаний, умений и навыков. ЛитератураА н а н ь е в Б. Г. О преемственности в обучении // Советская педагогика. – 1953. – № 2. – С. 23–35. Б а т а р ш е в А. В. Педагогическая система преемственности обучения в общеобразовательной и профессиональной школе. – СПб.: Изд-во Института профтехобразования РАО, 1996. – 90 с. Батаршев А. В. Преемственность обучения в общеобразовательной и профессиональной школе (теоретико-методологический аспект) / Под ред. А. П. Беляевой. – СПб.: Изд-во Института профтехобразования РАО, 1996. – 80 с. Блонский П. П. Развитие мышления школьника. – М.: Учпедгиз, 1935. – 128 с. Гальперин П. Я. Методы обучения и умственного развития ребенка. – М.: Педагогика, 1985. – 46 с. Ганелин Ш. А. Принципы дидактики в их взаимосвязи у классиков педагогики // Советская педагогика. – 1961. – № 5. – С. 121–134. Глассер У. Школы без неудачников. М.: «Просвещение», 1991-71. Ушинский К.Д. Избранные педагогические сочинения. М.: «Педагогика», 1974-569с. |
