Готовая работа другого человека. Фгбоу впо угту
 Скачать 499.17 Kb. Скачать 499.17 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ухтинский государственный технический университет» ФГБОУ ВПО «УГТУ» Воркутинский филиал УГТУ Кафедра недропользования, строительства и менеджмента Курсовой проект Дисциплина: Детали машин и основы конструирования Тема: Проектирование и расчёт одноступенчатого редуктора Шифр (202223) Группа ГД-20з-С Курс 3 Вариант № 28 Шамыкаев Александр Алексеевич Оценка: ______________ Проверил:____________ Хозяинов В.П. Дата проверки_________ г. Воркута 2023г. Оглавление1. Задание на проектирование. 2 2. Кинематический и силовой расчёт привода. 3 2.1 Выбор электродвигателя. 3 2.1.1 Требуемая мощность электродвигателя. 3 2.2 Передаточные отношения привода и отдельных его передач. 3 2.3 Частоты вращения, угловые скорости, мощности и моменты на валах привода. 4 2.3.1 Частоты вращения валов. 4 2.3.2 Угловые скорости валов. 4 2.3.3 Мощности на валах привода. 5 2.3.5 Максимальный момент при перегрузке на валу двигателя (вал 1) 5 6 3 Расчёт косозубой передачи редуктора. 6 3.1 Материалы зубчатых колёс и допускаемые напряжения. 6 3.1.1Материалы шестерни и колеса. 6 Задание не содержит ограничений на габариты привода, поэтому для зубчатых колёс назначаем материалы со средними механическими характеристиками: сталь 45, термическая обработка - улучшение по ГОСТ 1050 – 88. Материал шестерни и колеса должен иметь нижеследующие механические свойства по таблице 3.3, с.34/ Учебник Чернавский С.А. : 6 Для стальных колёс с твердостью менее НВ 350 /2, с.34/ / Учебник Чернавский С.А. : 7 3.2 Расчёт геометрических параметров косозубой передачи. 9 3.3 Проверочный расчёт прочности зубьев 12 Литература. 17 1. Задание на проектирование.Спроектировать привод ленточного конвейера, содержащий асинхронный электродвигатель, клиноременную передачу, одноступенчатый цилиндрический редуктор с косозубыми колёсами и стандартную компенсирующую муфту. Схема привода – на рисунке 1. Срок службы редуктора 36000 часов, привод реверсивный. Кратковременные перегрузки соответствуют максимальному пусковому моменту выбранного электродвигателя. М 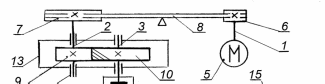 ощность Р4 = 6 кВт, передаваемая компенсирующей муфтой 11, при частоте вращения ощность Р4 = 6 кВт, передаваемая компенсирующей муфтой 11, при частоте вращения n4 = 80об/мин. 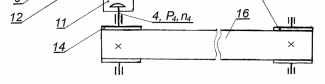 1 – вал электродвигателя; 2 – вал редуктора быстроходный; 3 – вал редуктора тихоходный; 4 – вал конвейера; 5 – электродвигатель; 6, 7 – шкивы клиноременной передачи ведущий и ведомый соответственно; 8 – ремень клиновой; 9, 10 – косозубые колёса редуктора; 11 – муфта компенсирующая; 12 – подшипники; 13 – корпус редуктора; 14,15 – барабаны конвейера ведущий и ведомый соответственно; 16 – лента конвейера. Рисунок 1.1 – Схема привода. 2. Кинематический и силовой расчёт привода.2.1 Выбор электродвигателя.2.1.1 Требуемая мощность электродвигателя.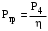 , (2.1) , (2.1)где Р4 – мощность на компенсирующей муфте (на выходе привода), кВт; η – КПД привода. Здесь: 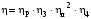 , (2.2) , (2.2)где ηР, ηЗ, ηп – соответственно КПД ременной, зубчатой передач, пары подшипников качения; η4 – КПД, учитывающий потери в опорах вала приводного барабана конвейера. Примечания. В формуле (2.2) принято, что КПД всех подшипников качения одинаковы. Руководствуясь рекомендациями /2, с.5/, принимаем ηР = 0,95; ηЗ = 0,97; ηп = 0,99; η4 = 0,99; После подстановки численных значений параметров в формулы (2.2) и (2.1), получим КПД привода: 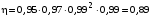 и требуемую мощность электродвигателя 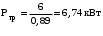 . .2.1.2 С учётом требуемой мощности Ртр = 6,74 кВт выбираем асинхронный двигатель трехфазный короткозамкнутый 4А132M6У3 серии 4А закрытый, обдуваемый, с номинальной мощностью Рном = 7,5 кВт, синхронной частотой вращения nс = 1000 об/мин, с учётом скольжения s = 3,5% и отношением пускового момента к номинальному 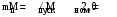 Вычисляем номинальную частоту вращения: 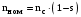 , (2.3) , (2.3)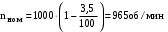 . .2.2 Передаточные отношения привода и отдельных его передач.Общее передаточное отношение привода при частоте вращения входного вала привода nдв = 965 об/мин. 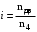 , (2.4) , (2.4)Расчёт по формуле (2.4) дает 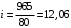 Примем /2, с. 6/ передаточное отношение для зубчатой пары – iзб = 4. Тогда на долю клиноременной передачи остается передаточное отношение: 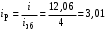 . .Проверка 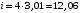 убеждает в правильности вычислений. убеждает в правильности вычислений.2.3 Частоты вращения, угловые скорости, мощности и моменты на валах привода.2.3.1 Частоты вращения валов.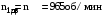 – частота вращения на валу двигателя; – частота вращения на валу двигателя;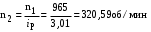 – частота вращения вала шкива клиноременной передачи; – частота вращения вала шкива клиноременной передачи; 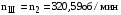 – частота вращения вала шестерни; – частота вращения вала шестерни;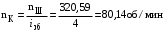 – частота вращения вала колеса; – частота вращения вала колеса;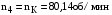 – частота вращения вала конвейера (выходного вала). – частота вращения вала конвейера (выходного вала).2.3.2 Угловые скорости валов.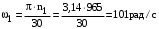 – угловая скорость вращения на валу двигателя; – угловая скорость вращения на валу двигателя;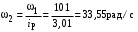 – угловая скорость вращения вала шкива клиноременной передачи; – угловая скорость вращения вала шкива клиноременной передачи;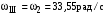 – угловая скорость вращения вала шестерни; – угловая скорость вращения вала шестерни;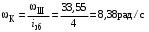 – угловая скорость вращения вала колеса; – угловая скорость вращения вала колеса;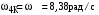 – угловая скорость вращения вала конвейера (выходного вала). – угловая скорость вращения вала конвейера (выходного вала).2.3.3 Мощности на валах привода.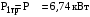 – мощность на валу двигателя; – мощность на валу двигателя;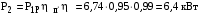 –мощность на быстроходном (ведущем) валу; –мощность на быстроходном (ведущем) валу;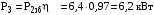 – мощность на тихоходном (ведомом) валу; – мощность на тихоходном (ведомом) валу;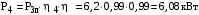 – мощность на валу конвейера. – мощность на валу конвейера.2.3.4 Вращающие моменты на валах привода. 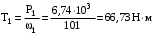 – вращающий момент на валу двигателя; – вращающий момент на валу двигателя;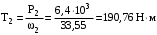 – вращающий момент на быстроходном (ведущем) валу; – вращающий момент на быстроходном (ведущем) валу;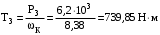 – вращающий момент на тихоходном (ведомом) валу; – вращающий момент на тихоходном (ведомом) валу;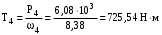 – вращающий момент на валу конвейера (выходном валу). – вращающий момент на валу конвейера (выходном валу).2.3.5 Максимальный момент при перегрузке на валу двигателя (вал 1)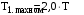 (см. пункт 2.1.3). (см. пункт 2.1.3).Номинальной мощности двигателя Рном = 3,0 кВт соответствует номинальный момент 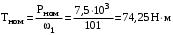 . .Отсюда, 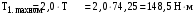 . .Очевидно, что при кратковременных перегрузках максимальные моменты на всех остальных валах будут превышать моменты, рассчитанные при передаче требуемой мощности (см. пункт 2.3.4) в 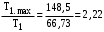 раза. раза.Исходя из этих соображений, получаем: 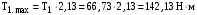 ; ;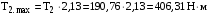 ; ;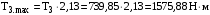 ; ;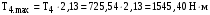 . .2.3.6 Результаты расчётов, выполненных в подразделе 2.3, сведены в таблице 2.1. Таблица 2.1 – Частоты вращения, угловые скорости, мощности и моменты навалах привода.
3 Расчёт косозубой передачи редуктора.3.1 Материалы зубчатых колёс и допускаемые напряжения.3.1.1Материалы шестерни и колеса.Задание не содержит ограничений на габариты привода, поэтому для зубчатых колёс назначаем материалы со средними механическими характеристиками: сталь 45, термическая обработка - улучшение по ГОСТ 1050 – 88. Материал шестерни и колеса должен иметь нижеследующие механические свойства по таблице 3.3, с.34/ Учебник Чернавский С.А. : Шестерня Колесо Твёрдость НВ 230…260 НВ 200…225 Предел текучести σТ, не менее 440 МПа 400 МПа Предел прочности σВ, не менее 750 МПа 690 МПа 3.1.2 Допускаемое контактное напряжение при расчёте зубьев на выносливость в общем случае /2, с.33/ 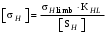 , (3.1) , (3.1)где 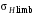 – предел контактной выносливости при базовом числе циклов, МП – предел контактной выносливости при базовом числе циклов, МП 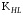 – коэффициент долговечности; – коэффициент долговечности; 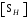 – коэффициент безопасности. – коэффициент безопасности.Для стальных колёс с твердостью менее НВ 350 /2, с.34/ / Учебник Чернавский С.А. :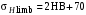 , (3.2) , (3.2)Коэффициент долговечности /2, с.33/ 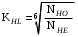 , (3.3) , (3.3)где 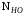 – базовое число циклов; – базовое число циклов;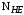 – эквивалентное (действительное) число циклов перемены напряжений. – эквивалентное (действительное) число циклов перемены напряжений.Для стали с твердостью НВ 200…500 значение базового числа циклов 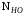 линейно возрастает от 107 до 6·107 /2, с.34/. линейно возрастает от 107 до 6·107 /2, с.34/.Эквивалентное (действительное) число циклов /3, с.184/ 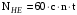 , (3.4) , (3.4)где с – число зубчатых колес, сцепляющихся с рассматриваемым колесом; n – частота вращения этого колеса, об/мин; t – срок службы передачи в часах. Для шестерни и колеса c = 1, n2 = 32,99 об/мин, n3 = 80,14 об/мин. По заданию на курсовой проект (см. раздел 1) срок службы составляет 36000 часов. Расчёт по формуле (3.4) даёт для шестерни и колеса соответственно: 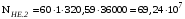 , ,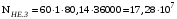 . .Без вычислений по формуле (3.3) видно, что коэффициент долговечности для каждого из колёс окажется меньше единицы, так как 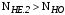 и и 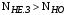 . .В таком случае следует принимать 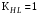 /2, с.33/. /2, с.33/.Если взять коэффициент безопасности 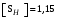 (для улучшенной стали) /2, с.33/, то расчёт по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно (для улучшенной стали) /2, с.33/, то расчёт по формулам (3.1) и (3.2) даст допускаемые контактные напряжения для шестерни и колеса соответственно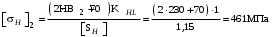 , ,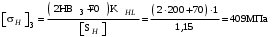 . .В частном случае для косозубых передач допускаемое контактное напряжение при расчёте на выносливость /2, с.35/ 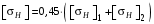 , (3.5) , (3.5)при соблюдении условия 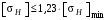 , где , где 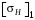 и и 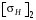 – соответственно допускаемые контактные напряжения для шестерни и колеса, вычисленные по формуле (3.1), МПа; – соответственно допускаемые контактные напряжения для шестерни и колеса, вычисленные по формуле (3.1), МПа;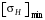 – меньшее из двух напряжений, входящих в правую часть формулы (3.5), МПа. – меньшее из двух напряжений, входящих в правую часть формулы (3.5), МПа.Расчёт по формуле (3.5) даёт 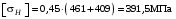 . .Условие 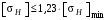 выполняется, так как выполняется, так как 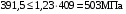 . .3.1.3 Допускаемое контактное напряжение при кратковременных перегрузках для колёс из улучшенной стали зависит от предела текучести и вычисляется по формуле /3, с.187/: 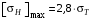 , (3.6) , (3.6)При σТ = 400 МПа (минимальное значение для колеса по пункту 3.1.1) 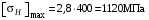 . .3.1.4 Допускаемые напряжения изгиба при проверочном расчёте зубьев на выносливость вычисляются по формуле /3, с.190/: 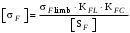 , (3.7) , (3.7)где 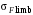 – предел выносливости материала зубьев при отнулевом цикле, соответствующий базовому числу циклов, МПа; – предел выносливости материала зубьев при отнулевом цикле, соответствующий базовому числу циклов, МПа; 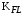 – коэффициент долговечности при расчёте зубьев на изгиб; – коэффициент долговечности при расчёте зубьев на изгиб; 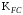 – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи); – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья (в случае реверсивной передачи); 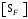 – допускаемый коэффициент безопасности (запаса прочности). – допускаемый коэффициент безопасности (запаса прочности).По рекомендации /2, с.43…45/ берём: – для улучшенных сталей 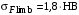 ; – при одностороннем нагружении зубьев, принимая привод нереверсивным ; – при одностороннем нагружении зубьев, принимая привод нереверсивным 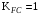 ; – для стальных поковок и штамповок при твёрдости менее НВ 350 ; – для стальных поковок и штамповок при твёрдости менее НВ 350 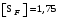 . .Коэффициент долговечности /3, с.191/ 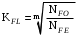 , (3.8) , (3.8)где m – показатель корня; 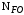 – базовое число циклов; – базовое число циклов;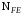 – эквивалентное (действительное) число циклов перемены напряжений. – эквивалентное (действительное) число циклов перемены напряжений.Для колёс с твёрдостью зубьев до и более НВ 350 величина m равна соответственно 6 и 9. Для всех сталей принимается 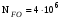 . .Для обоих колёс 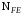 имеет те же численные значения, что и имеет те же численные значения, что и 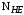 (см. пункт 3.1.2). Оба эти значения (для шестерни – 86,4·107, для колеса – 17,28·107) больше (см. пункт 3.1.2). Оба эти значения (для шестерни – 86,4·107, для колеса – 17,28·107) больше 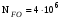 . .Поэтому, принимается коэффициент долговечности 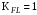 /3, с.191, 921/. /3, с.191, 921/.Расчёт по формуле (3.7) даёт соответственно для шестерни и колеса 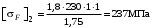 , , 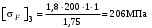 . .3.1.5 Допускаемое напряжение изгиба при расчёте зубьев на кратковременные перегрузки при твёрдости менее НВ 350 /2, с.193/ 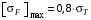 , (3.9) , (3.9)Расчёт по этой формуле с учётом характеристик материала (см. 3.1.1) даёт для шестерни и колеса соответственно 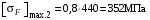 , , 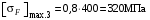 . .3.2 Расчёт геометрических параметров косозубой передачи.Межосевое расстояние цилиндрической зубчатой передачи из условия контактной выносливости активных поверхностей зубьев /2, с.32/ 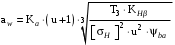 , (3.10) , (3.10)где 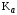 – коэффициент, равный 43 для косозубых колёс; u – передаточное число зубчатой пары; Т3 – момент на колесе (на большем из колёс), Н·м; – коэффициент, равный 43 для косозубых колёс; u – передаточное число зубчатой пары; Т3 – момент на колесе (на большем из колёс), Н·м;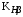 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца; 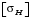 – допускаемое контактное напряжение, МПа; – допускаемое контактное напряжение, МПа; 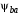 – коэффициент ширины венца по межосевому расстоянию. – коэффициент ширины венца по межосевому расстоянию.Передаточное число 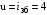 , а момент Т3 = 739,85 Н·м (см. раздел 2). Допускаемое напряжение , а момент Т3 = 739,85 Н·м (см. раздел 2). Допускаемое напряжение 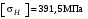 вычислено в пункте 3.1.2. вычислено в пункте 3.1.2.Коэффициент ширины венца по межосевому расстоянию 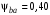 возьмём по рекомендации /2, с.33/ для косозубых передач. При несимметричном расположении колёс относительно опор принимаем ориентировочно возьмём по рекомендации /2, с.33/ для косозубых передач. При несимметричном расположении колёс относительно опор принимаем ориентировочно 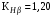 /2, с.32/.В итоге расчёт по формуле (3.10) даёт /2, с.32/.В итоге расчёт по формуле (3.10) даёт 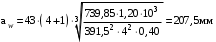 . Межосевое расстояние округляем до стандартного значения 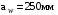 /2, с.36/. /2, с.36/.Нормальный модуль /2, с.36/ 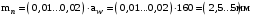 . .Из стандартного ряда модулей /2, с.36/ берём 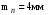 . .Назначим предварительно угол наклона линии зуба для косозубых колёс β = 10° /2, с.37/. Тогда, суммарное число зубьев 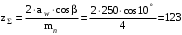 . .Определяем число зубьев шестерни: 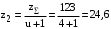 Принимаем z2 = 24, тогда число зубьев колеса 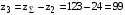 . .Фактическое передаточное отношение 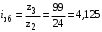 . .Расхождение с принятым ранее номинальным передаточным отношением 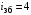 составляет составляет 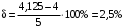 , что допустимо (не превышает 3%). , что допустимо (не превышает 3%).Уточнённое значение 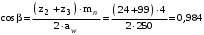 соответствует β = 10,2631° = 10°15'47" Кинематическая схема исследуемого редуктора приведена на рисунке 3.1 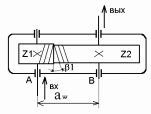 Рис. 3.1. Кинематическая схема одноступенчатого цилиндрического редуктора с косозубой передачей. Косозубые цилиндрические передачи целесообразно проверять на выполнение условия /2, с.36/ 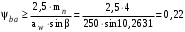 . .При принятом значении коэффициента ширины венца по межосевому расстоянию 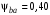 условие выполняется. условие выполняется.При обработке шестерни с числом зубьев z2 = 24 подрезание зубьев исключается, так как условие неподрезания /2, с.38/ 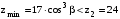 соблюдено, что видно и без расчёта 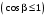 . .Делительные диаметры шестерни и колеса соответственно 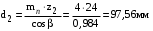 , , 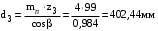 . .Правильность вычислений подтверждается проверкой 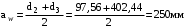 , что верно. , что верно.Диаметры вершин зубьев 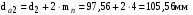 , ,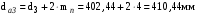 . .Диаметры впадин зубьев 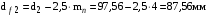 , ,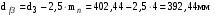 . .Ширина колеса 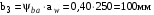 . .Ширина шестерни 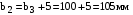 . .Коэффициент ширины шестерни по диаметру 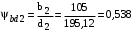 . .3.3 Проверочный расчёт прочности зубьев3.3.1 Расчётное контактное напряжение для косозубых цилиндрических передач /2, с.31/ 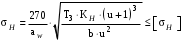 , (3.11) , (3.11)где 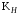 – коэффициент нагрузки; b – ширина колеса расчётная (наименьшая). – коэффициент нагрузки; b – ширина колеса расчётная (наименьшая).Остальные символы в формуле расшифрованы ранее. Окружная скорость колёс 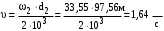 . .При такой скорости  назначаем восьмую степень точности /2, с.32/. назначаем восьмую степень точности /2, с.32/.Коэффициент нагрузки /2, с.32/ при проверочном расчёте на контактную прочность 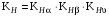 , (3.12) , (3.12)где 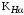 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; 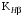 – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца); – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца);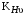 – коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент). – коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент).По рекомендациям /2, с.39, 40/ назначаем следующие значения перечисленных коэффициентов: 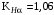 при окружной скорости при окружной скорости 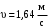 и восьмой степени точности; и восьмой степени точности; 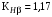 при значении коэффициента при значении коэффициента 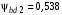 , твёрдости зубьев менее НВ 350 и несимметричном расположении колёс относительно опор; , твёрдости зубьев менее НВ 350 и несимметричном расположении колёс относительно опор; 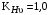 при окружной скорости при окружной скорости 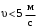 , восьмой степени точности и твёрдости менее НВ 350. , восьмой степени точности и твёрдости менее НВ 350.Расчёт по формуле (3.1) даёт 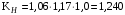 . .Ширину колеса берём в расчёт минимальную b = 100 мм. Момент на колесе Т3 = 739,85 Н·м. Расчёт по формуле (3.11) даёт 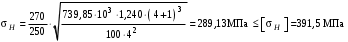 . .Условие прочности выполняется. Недогрузка составляет 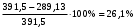 . Она объясняется увеличением первоначально вычисленного межосевого расстояния до стандартного . Она объясняется увеличением первоначально вычисленного межосевого расстояния до стандартного 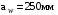 . .3.3.2 Расчёт зубьев на контактную прочность по формуле (3.11) при кратковременных перегрузках моментом 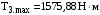 (см. раздел 2) даёт (см. раздел 2) даёт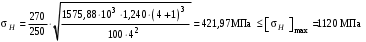 (см.пункт 3.1.3). 3.3.3 Напряжения изгиба зубьев косозубых цилиндрических колёс при проверочном расчёте на выносливость вычисляются по формуле /2, с.46/ 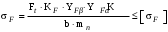 , (3.13) , (3.13)где 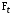 – окружная сила, Н; – окружная сила, Н; 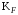 – коэффициент нагрузки; – коэффициент нагрузки;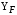 – коэффициент формы зуба; – коэффициент формы зуба;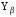 – коэффициент, компенсирующий погрешности, возникающие из–за применения для косых зубьев той же расчётной схемы, что и для прямых; – коэффициент, компенсирующий погрешности, возникающие из–за применения для косых зубьев той же расчётной схемы, что и для прямых;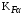 – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями; – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;b – ширина колеса, находящаяся в зацеплении (минимальная), мм; 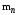 – модуль нормальный, мм. – модуль нормальный, мм.В зацеплении колес косозубой передачи действуют следующие силы /2, с.158/: – окружная 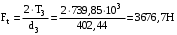 ; ;– радиальная 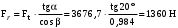 ; ;– осевая 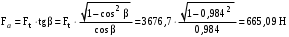 . .(Здесь α – угол зацепления в нормальном сечении (ГОСТ 13755-81)) . Коэффициент нагрузки /2, с.42/: 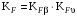 , (3.14) , (3.14)где 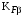 – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца); – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца); 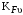 – коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент). Принимаем – коэффициент, учитывающий дополнительные динамические нагрузки (динамический коэффициент). Принимаем 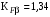 /2, с.43/ с учётом, что твёрдость колёс менее НВ 350, коэффициент /2, с.43/ с учётом, что твёрдость колёс менее НВ 350, коэффициент 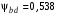 , а каждое из колёс расположено несимметрично относительно опор. Назначим , а каждое из колёс расположено несимметрично относительно опор. Назначим 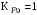 , учитывая дополнительно, что окружная скорость υ = 1,64 м/с < 3 м/с, а степень точности принята восьмая. , учитывая дополнительно, что окружная скорость υ = 1,64 м/с < 3 м/с, а степень точности принята восьмая.Тогда, по формуле (3.14) 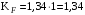 . .Без расчётов, руководствуясь только рекомендацией /2, с.47/, возьмём 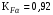 . .Коэффициент 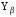 определим по формуле /2, с.46/ определим по формуле /2, с.46/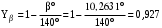 (Здесь β° – вычисленный ранее угол наклона зубьев). Коэффициент формы зуба 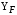 для косозубых колёс зависит от эквивалентного числа зубьев /2, с.46/, которое составляет: для косозубых колёс зависит от эквивалентного числа зубьев /2, с.46/, которое составляет:для шестерни 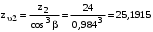 , ,для колеса 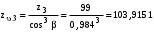 . .Для эквивалентных чисел зубьев соответственно шестерни и колеса находим /2, с.42/ 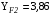 и и 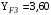 . .Подстановка подготовленных численных значений в формулу (3.13) даёт для шестерни и колеса соответственно: 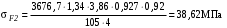 ; ;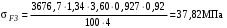 . .Это значительно меньше вычисленных в пункте 3.1.4 допускаемых напряжений 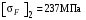 и и 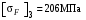 . .Результат расчёта свидетельствует о большой недогрузке зубьев по напряженности изгиба. Это характерно для колес с малой твердостью и не являются отрицательным результатом проверочного расчёта. Ведь все геометрические параметры колёс определены проектным расчётом по контактным напряжениям. 3.3.4 Напряжения изгиба при кратковременных перегрузках вычисляются также по формуле (3.13), куда вместо окружной силы Ft, рассчитанной для длительно передаваемой мощности, следует подставить окружную силу при кратковременных перегрузках 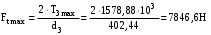 . .После подстановки в формулу (3.13) получаем при перегрузках соответственно для шестерни и колеса напряжения изгиба 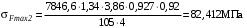 ; ;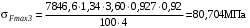 . .Эти напряжения значительно меньше вычисленных в пункте 3.1 допускаемых напряжений 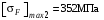 и и 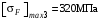 . .3.3.5 Геометрические параметры колёс косозубой передачи, обоснованные в результате расчётов, сведены в таблицу 3.1. Таблица 3.1 – Геометрические параметры колес зубчатой передачи
Литература.Чернавский С.А Устюгов И.И. 1981 Жингаровский А.Н. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
