вращ. Физические основы механики кинематика 1 Механическое движение

• Название: Физические основы механики кинематика 1 Механическое движение
• Дата: 23.04.2021
• Размер: 394.58 Kb.
• Имя файла: вращ.docx
• Тип: Закон; #197933

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

КИНЕМАТИКА

§1 Механическое движение

Простейшим видом движения в природе является механическое движение, состоящие в изменении взаимного расположения тел или их частей в пространстве с течением времени. Раздел физики, занимающийся изучением закономерностей механического движения, называетсямеханикой.

Различают классическую механику, когда скорость макроскопических тел существенно меньше скорости света. Классическая механика основана на законах Ньютона, поэтому его часто называют ньютоновской механикой. Движения тел со скоростями близкими к скорости света изучается в релятивистской механике, а закономерности движения микрочастиц в квантовой механике.

Классическая механика состоит из трех основных разделов – статики, кинематики и динамики. Статика – изучает законы сложения сил и условия равновесия тел. Кинематика (движение) – дает математическое описание движения тел без учета причин, вызывающих это движение.Динамика – изучает движение тел с учетом действующих на них сил.

§2 Система отсчета. Материальная точка.

Перемещение, путь, траектория.

 

   Движением в механике называется изменение взаимного расположения тел. Для описания движения тел необходимо предварительно выбрать систему отсчета, т.е. выбрать одно или несколько тел, которые условно принимаются за неподвижные, и с ними связать какую-либо координатную систему и часы.

   Абсолютно твердым телом называется тело, деформацией которого в условиях данной задачи можно пренебречь. Расстояние между любыми двумя точками абсолютно твердого тела не изменяется при любых взаимодействиях.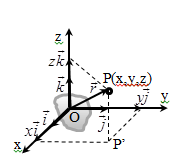

    Тело, по отношению к которому рассматривается движение других тел, называется телом отсчета.

   Наиболее часто используется прямоугольная, декартова система координат, образованная тремя взаимно перпендикулярными осями  X, Y, Z.

Единичные вектора вдоль этих осей называются ортами- . Их откладывают из начала координат О. Положения произвольной точки Р характеризуется радиус вектором  ,соединяющим начало координат О с точкой Р.



X, Y, Z – декартовы координаты точки P или проекции радиус-вектора  на соответствующие оси координат. Характер движения тела в пространстве будет задан, если мы будем знать, как меняются во времени координаты или его радиус-вектор, т.с. будут определены зависимости x=x(t); y=y(t);

Решая физическую задачу некоторыми факторами, которые в данной задаче не существенные, пренебрегают, например, часто можно пренебречь размерами тела, движения которого изучается.

   Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.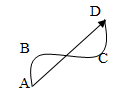

    Линия, описываемая материальной точкой при её движении в пространстве, называется траекторией. Расстояние между двумя положениями точки, измеренное вдоль траектории называется путем, пройденным телом. (Путь – длина траектории.)

Вектор, соединяющий начальное положение тела с конечным положением, называется вектором перемещения.

ABCD – траектория

 - перемещение

 

В зависимости от формы траектории различают прямолинейное и криволинейное движение точки.

Если траектория тела представляет прямую линию, то движение – прямолинейное, кривую – криволинейное.

Кроме этого различают поступательное и вращательное движение.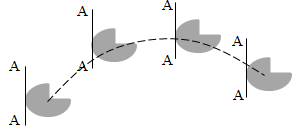


 Движение тела называется поступательным, если любая прямая, проведенная в теле, остается при движении этого тела параллельной самой себе (при этом движении траектории всех точек тела одинаковые).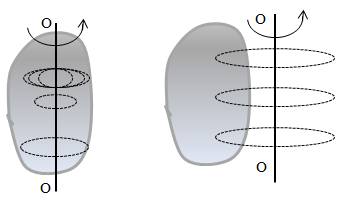


 При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения; ось вращения может находиться вне тела.

§3 Скорость

   Средней скоростью на каком-либо участке траектории называется отношение приращения радиус-вектора   точки за промежуток времени t+ Δt к его продолжительности Δt.



   (Средней скоростью тела на каком-либо участке траектории называется отношение длины S этого участка ко времени t, в течение которого тело прошло этот  участок.)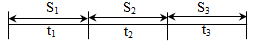

    Если для участков любой длины, взятых в различных местах траектории, это отношение одинаково, то скорость тела вдоль траектории постоянна и такое движение называется равномерным.

 

 





   Скоростью (мгновенной скоростью) точки называется векторная величина  , равная первой производной по времени от радиуса-вектора  рассматриваемой точки:



   (Скорость точки в момент времени t равна пределу средней скорости v_ср при Δt→0)



В 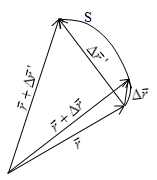общем случае путь S отличен от модуля перемещения |Δr|. Одинаково, если рассматривать путь dS, проходимый точкой за малый промежуток времени dt, то  dS=|dr|. Поэтому модуль вектора скорости равен первой производной от длины пути по времени:

Средней путевой скоростью неравномерного движения точки на данном участке ее траектории называется скалярная величина Vср равная отношению длины этого участка, траектории к продолжительности  ?t прохождения его точкой



Вектор скорости можно представить в виде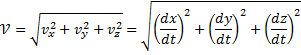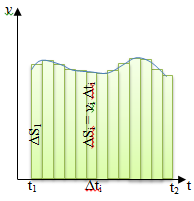









    Вектор   скорости точки направлен по касательной к траектории  в сторону движения также и вектор    малого перемещения точки за весь промежуток времени   (то что вектор направлен по касательной следует из физического смысла первой производной - это касательная к графику функции, показывает скорость движения в момент времени  ).

   Вычислим путь, проходимый телом за время t₁ - t₂ в случае неравномерного движения.

   Разобьем промежуток времени t₁ - t₂ на N малых одинаковых промежутков. Весь путь пройденный телом можно найти, сложив все элементарные пути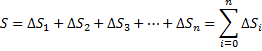





тогда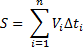



Если  , то мы найдем значение   :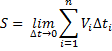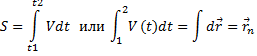                                                       




§4 Ускорение.

Тангенциальная и нормальная  составляющие ускорения

 

   Ускорение – векторная величина, характеризующая быстроту изменения скорости движущегося тела по величине и направлению.

   Средним ускорением точки в интервале времени Δt называется вектор а_ср, равный отношению приращения вектора скорости ΔV к промежутку Δt.



   Ускорением (мгновенным ускорением) точки называется векторная величина a, равная первой производной скорости v по времени (или вторая производная радиус - вектора   по времени):



  Ускорение точки в момент времени t равно пределу среднего ускорения   при 



   В декартовой системе координат вектор   можно записать через его координаты:

, где



Модуль вектора ускорения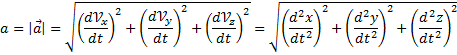



Вектор   можно представить в виде суммы двух составляющих:

- тангенциальная составляющая ускорения направлена по касательной к траектории точки и равна



г 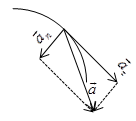де вектор   – единичный вектор касательной, проведенной в точке траектории и направлении скорости

Векторы   и   сонаправлены при равноускоренном движении;   при   т.е. при равнозамедленном движении.

Касательное ускорение   - характеризует быстроту изменения модуля вектора скорости точки (характеризует изменение скорости по величине).

Для равномерного движения: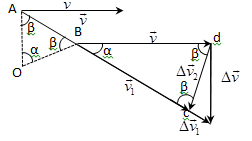          




-нормальная составляющая ускорения (нормальное ускорение) направлена по нормали к траектории и рассматриваемой точке в сторону к центру кривизны траектории. Криволинейную траекторию можно представить как совокупность элементарных участков, каждый из которых может рассматриваться как дуга окружности некоторого радиуса R (называемого радиусом кривизны кривой в окружности данной точки траектории)







  Нормальное ускорение характеризует быстроту изменения направления вектора скорости (характеризует изменение скорости по направлению).

Модуль полного ускорения:

                           

Классификация движений зависит от тангенциальных и нормальных составляющих:

1)

2)                  

3)  

4)

5)

6)  



7)  

§5 Кинематика вращательного движения

Поворот тела на некоторый угол φ можно описать с помощью вектора, длина которого равна φ, а направление совпадает с осью вращения и определяется по правилу правого винта (буравчика, правой руки):

Ч 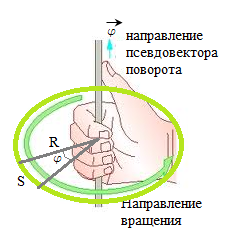етыре пальца правой руки – по направлению вращения, согнутый большой палец укажет направление вектора  .

Направление вектора поворота φ, связывается с направлением вращения правилом правой руки. Такие векторы называют аксиальными (осевыми) или псевдовекторами, чтобы подчеркнуть их отличие от обычных (иногда называемых полевыми) векторов. Угловой скоростью называют вектор   который численно равен первой производной от угла поворота   по времени t и направлен вдоль неподвижной оси по правилу правой руки.

 

 



У 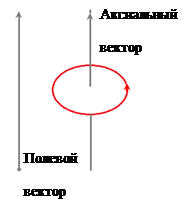гловая скорость  , как и  является аксиальным вектором. Аксиальные векторы не имеют определённых точек приложения, они могут откладываться из любой точки оси вращения. Часто их откладывают от неподвижной точки оси вращения, принимаемой одновременно за начало координат системы отчёта. Вращение тела называют равномерным, если  .

 



Скорость   точки в отличие от угловой скорости  , тела называют линейной скоростью. Она направлена перпендикулярно как к оси вращения (т.е. к вектору  ), так и радиус - вектору  R, проведённому в точку Р из центра окружности О и равна их векторному произведению:



Р 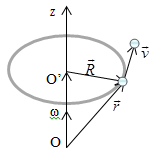авномерное вращение можно  характеризировать периодом вращения Т, под которым понимают время, за которое тело делает один оборот, т.е. поворачивается на угол  . Тогда   - связь угловой скорости с периодом обращения.

Частота вращения - число оборотов в единицу времени         ;    .

В случае переменного вращательного движения угловая скорость          материальной точки не изменяется как по величине, так и по направлению. Для характеристики быстроты изменения вектора угловой скорости    при неравномерном вращении вокруг неподвижной оси вводится вектор         углового ускорения тела, равный первой производной от его угловой скорости    по времени.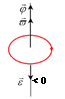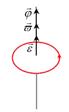



Вектор   так же является аксиальным (или псевдовектором). Векторы   и    сонаправлены при ускоренном вращении ( ) и            противоположно направлены при замедленном вращении.

 ( )

Ускорение   произвольной точки Р тела в отличие от углового ускорения   тела называет линейным ускорением.



 



Для равноускоренного вращательного движения можно записать:



Связь линейных и угловых величин:                        

                               

 

 ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

§1 Первый закон Ньютона

  Инерциальные системы отсчета

 

     1-й закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет его из этого  состояния.

     -    I закон  Ньютона

 

       Этот закон называют законом инерции. Инерция - способность тела сохранять скорость. Движение по инерции - движение с постоянной скоростью.

       1-й закон Ньютона выполняется не во всех системах отсчета.  Системы отсчета, в которых выполняется 1-й закон Ньютона, называются инерциальными. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.

П 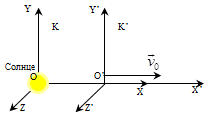римером инерциальной системы отсчета может служить гелиоцентрическая система отсчета, т. е. система отсчета, связанная с  Солнцем.

Любая система отсчета, движущаяся относительно гелиоцентрической равномерно и прямолинейно будет являться инерциальной.

Лабораторная система отсчета, оси координат которой жестко связаны с Землей, неинерциальная из-за суточного вращения Земли. Однако вращение Земли происходит очень медленно с а=0,034 м/с², и поэтому в большинстве задач лабораторную систему отсчета можно приближенно считать инерциальной.

Содержание 1-го з. Н. сводится к двум утверждениям:

1) все тела обладают свойством инертности;

2) существуют инерциальные системы отсчета.

Инерциальные системы отсчета играют особую роль не только в механике, но и в других  разделах физики, т. к. согласно принципу относительности Эйнштейна математическая запись любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчета.

 

§2  Масса, импульс тела.

2-й закон Ньютона

Одинаковое воздействие по-разному изменяет движение различных тел. При воздействии всякое тело изменяет свою скорость не сразу, а постепенно. Способность тела сохранять свою скорость называется инертностью. Мерой инертностью является масса. Масса тела – положительная скалярная  величина, являющаяся мерой инертности тела, т. е. характеризует способность тела сохранять свою скорость.

Под действием силы тело изменяет свою скорость не мгновенно, а постепенно, т. е. приобретает конечное ускорение, которое тем меньше, чем больше масса, т. е. при воздействии одной и той же силы  .

Плотность тела ровна отношению массы dm малого объёма    к величине этого объёма  , если тело однородно, то   и  .

 

Центром инерции, или центром масс, системы материальных точек называется точка С радиус-вектор  , который равен                      



Векторная величина         равная произведению массы m материальной точки на ее скорость называется импульсом (или количеством движения) этой материальной точки    



     Импульсом системы материальных точек называется вектор  , равный геометрической сумме (т. е. сумме векторов) всех материальных точек



     Скорость центра инерции:



т. е. импульс системы равен произведению массы всей системы на скорость ее центра инерции:     

 

     2-й закон Ньютона: скорость изменения импульса        тела равна действующей на тело силе F         

          - 2-й закон Ньютона

    Если на тело действует несколько сил, то под силой F во втором законе Ньютона нужно понимать равнодействующую силу -геометрическую сумму всех сил, действующих на тело.

     Из второго закона Ньютона следует, что 

     Векторная величина Fdt называется элементарным импульсом силы.

     Импульс силы за конечный промежуток времени t₂-t₁ равен   , где 

            

 

 

     

 



 

   



 

       Сила, действующая на тело, равна произведению массы тела на его ускорение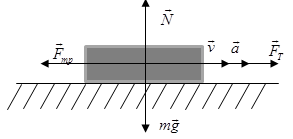









x: 

y: -mg + N=0

Касательное и нормальное ускорение определяются соответствующими составляющими силы F

            

 



              

 

 

   Сила F_n, сообщающая точке нормальное ускорение, направлена к центру кривизны траектории и потому называется центростремительной силой.

 

§3 Третий закон Ньютона

 

Всякое действие тела друг на друга  носит характер взаимодействия: если тело 1 действует на тело 2 с силой F21, то и тело 2 действует на тело 1 с силой F12.

ІІІ закон Ньютона: силы, с которыми действуют друг на друга взаимодействующие тела равны по величине и противоположны по направлению.( сила действия равна силе противодействия )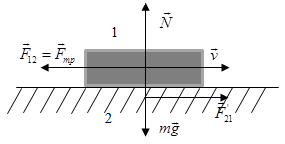        

 

 



ІІІ закон Ньютона справедлив не всегда. Он строго выполняется в случае контактных взаимодействий, а также при взаимодействии находящихся на некотором расстоянии друг от друга покоящихся тел.

      Из ІІІ закона Ньютона следует, что в любой механической системе геометрическая сумма всех внутренних сил ровна 0





 

 

      ІV. Закон всемирного тяготения: Два точечных тела притягиваются друг к другу через пространство с силой, прямо пропорционально их инертным массам и обратно пропорциональной квадрату расстояния между ними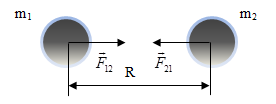

 

                                      γ=6,672

 


    γ - гравитационная постоянная (численно равная силе взаимного тяготения 2-х материальных точек единичной массы находящихся на расстоянии 1 м.)

 

§4 Закон сохранения импульса

 

      Рассмотрим систему состоящую из n материальных точек, взаимодействующих между собой.





 

Силы взаимодействия между телами, образующими систему, обозначим fk. Взаимодействие внешних сил со стороны тел не входящих в данную систему на і-тое тело системы обозначим Fi.

       Запишем  ІІ закон Ньютона применительно ко всем телам, образующим систему:





 





по III закону Ньютона

 

   



      Векторная сумма импульсов всех тел, образующих данную систему называется результирующим импульсом системы.



      Если внешние силы не действуют на тела системы (нет взаимодействия между телами, входящими в систему и внешними телами), или действие внешних сил скомпенсирована, то система называется замкнутой или изолированной.

     В этом случае



 

 

   Закон сохранения импульса:

геометрическая (векторная) сумма импульсов замкнутой системы остаётся постоянной с течением времени при любых взаимодействиях внутри системы:

 

З. С. И.          


т. е. в результате взаимодействия между телами системы импульсы отдельных тел могут изменяться как по величине, так и по направлению, но в таких рамках, что векторная сумма импульсов всех тел, образующих данную систему остаётся величиной постоянной.

Пример 1: абсолютно упругий удар

 

З.С.И:  .       

 



Проекция на ось x: 

Пример 2: Упругий удар шара об неподвижную стенку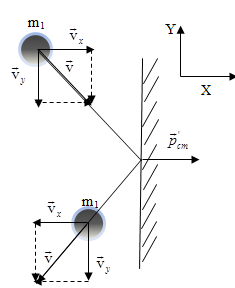

 

 

                                                                                                                                            

 



 

                                                                   
§5 Сила. Виды сил

 

      В механике рассматриваются два вида воздействия на тело со стороны других тел.

1) данное тело под воздействием других тел изменяет свою скорость, т. е. приобретает ускорение.

2) данное тело под воздействием других тел деформируются, т. е. изменяет свою форму и размеры

       Для описания этих воздействий пользуется понятием силы: 

Сила - векторная величина является мерой механического действия на рассматриваемое тело со стороны других тел.

      Силы, сообщающие телам ускорение или деформирующие  их, можно разделить на две группы:

а) силы распределения по объёму тела, например силы тяготения.

Для таких сил характерно, что каждая элементарная часть тела испытывает действие силы независимо от наличия  или отсутствия соседних частей тела.

б) силы сосредоточенные, т.е. приложенные к определённому месту тела – в точке, вдоль некоторой линии или поверхности тела. В этом случае действие внешней силы передается от одних частей к другим благодаря существованию взаимной связи между ними (это привод к деформации).

 

 

    I  Упругие силы.

     Под действием сил, приложенных к телу, оно деформируется. Если после прекращения действия сил тело принимает первоначальные размеры и форму, то деформация называется упругой, а если не восстанавливает форму и размеры, то деформация - неупругая. Упругие деформации наблюдаются, если приложенная сила меньше предельной силы, при которой наступает неупругая деформация (так называемой предел упругости)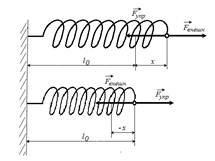

    

   Рассмотрим пружину один конец которой закреплен, а ко второму приложена растягивающая (или сжимающая) сила Fвн.

Из опыта следует, что при небольших деформациях удлинение пружины X прямо пропорционально растягивающей силе.



 

   

 

 

Закон Гука: сила упругости F_упр. прямо пропорциональна деформации (смещению) X. Коэффициент пропорциональности в законе Гука называют коэффициентом жесткости пружины - k.

Стержень ведёт себя подобно пружине. Если к концам стержня приложить равные F1 = F2 = F равномерно распределенные по поверхности S стержня силы, направленные вдоль его оси, то первоначальная длина стержня   изменится на  . Для характеристики деформации стержня вводят относительное изменение его длины  - относительная деформация.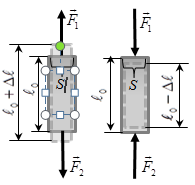

 

    Физическая величина, численно равная упругой силе dFупр., приходящейся на единицу площади dSсечения тела называется напряжением.

 



   Если сила dF_упр. направлена по нормали к площадке dS, напряжение называется нормальным и обозначается σ. Если dF_упр. направлена по касательной к площадке dS -  касательным и обозначается τ.

   Закон Гука (для стержня): напряжение упруго деформированного тела прямо пропорционально его относительной деформации.

 

G=E закон Гука.

    Модуль Юнга Е-модуль упругости, численно равный напряжению, которое возникает при относительной деформации, равной единице. Величина        называется коэффициентом упругости.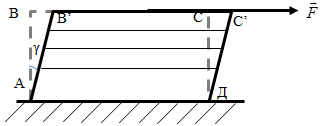





    Сдвигом называется деформация тела, при которой все его плоские слои параллельные некоторой плоскости  сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу.

При малом сдвиге         



- абсолютный сдвиг

γ - угол сдвига или относительный сдвиг выражений в радианах.

 

                 

 

  G-модуль сдвига- равен касательному напряжению при относительном сдвиге  tg γ=1, следовательно, γ =   

(хотя, практически все вещества разрушаются при значительно  меньших углах).

 

ІІІ. Сила тяжести и вес

 

Под действием силы притяжения к Земле все тела падают с одинаковым относительно поверхности  Земли ускорением g = 9.8 м/c² - ускорение свободного падения. Следовательно, на всякое тело массы m действует сила, называемая силой тяжести.

                                         =

(вращение Земли не учитываем)

   Сила тяжести вызывает падение незакрепленных тел на Землю. Она равна силе, с которой неподвижное относительно Земли тело давит на горизонтальную опору (или действует на вертикальный подвес) вследствие тяготения к Земле. Точка приложения силы тяжести тела, т.е. точка приложения равнодействующих сил тяжести всех частиц тела, называется центром тяжести тела. Центр тяжести тела совпадает с его центром инерции и в телах правильной геометрической формы определяется как наиболее симметричная точка в телах неправильной геометрической формы как точка равновесия (момент сил относительно центра тяжести при равновесии должен быть равен 0).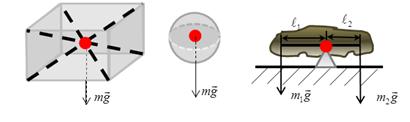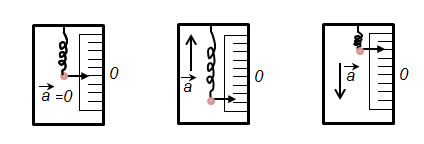




     Сила   , с которой тело действует на подвес или опору, называется весом тела. Если тело не подвижно относительно Земли (v=0), то  . Если тело и опора движутся с каким-нибудь ускорением относительно Земли, то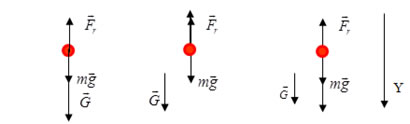 

 

  

 

 

2-й Закон Ньютона m +  .

По 3-му закону Ньютона  
Тогда





=

Проекция на ось Y

I Система покоится

Y:  mg – F_r = 0

G = mg

Вес равен силе тяжести.

II Система движется с ускорением вверх

Y:  mg – F_r = -ma

G = m(g + a)

Вес больше силы тяжести.

III Система движется с ускорением вниз

Y:  mg – F_r = ma

G = m (g - a)

Вес меньше силы тяжести