лекция. Лекция 07. Лекция 7 Элементы специальной теории относительности. Постулаты Эйнштейна
 Скачать 0.65 Mb.
|
Лекция № 7Элементы специальной теории относительности. Постулаты Эйнштейна Это современная физическая теория пространства и времени, в которой предполагается, что время однородно, а пространство однородно и изотропно. Преобразования координат Галилея – механический принцип относительности для инерциальных систем. Классическое правило сложения скорости. Эксперименты – абсолютное пространство, мировой эфир. В основе специальной теории относительности лежат два постулата Эйнштейна: 1. Принцип относительности: Никакие опыты, проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно, прямолинейно, все законы природы инвариантны по отношению к переходу от одной инерциальной системы к другой. 2. Принцип инвариантности скорости света: Скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Из этих постулатов следует относительность длины, относительность времени, относительность одновременности. Классические преобразования Галилея несовместимы с постулатами Эйнштейна. П 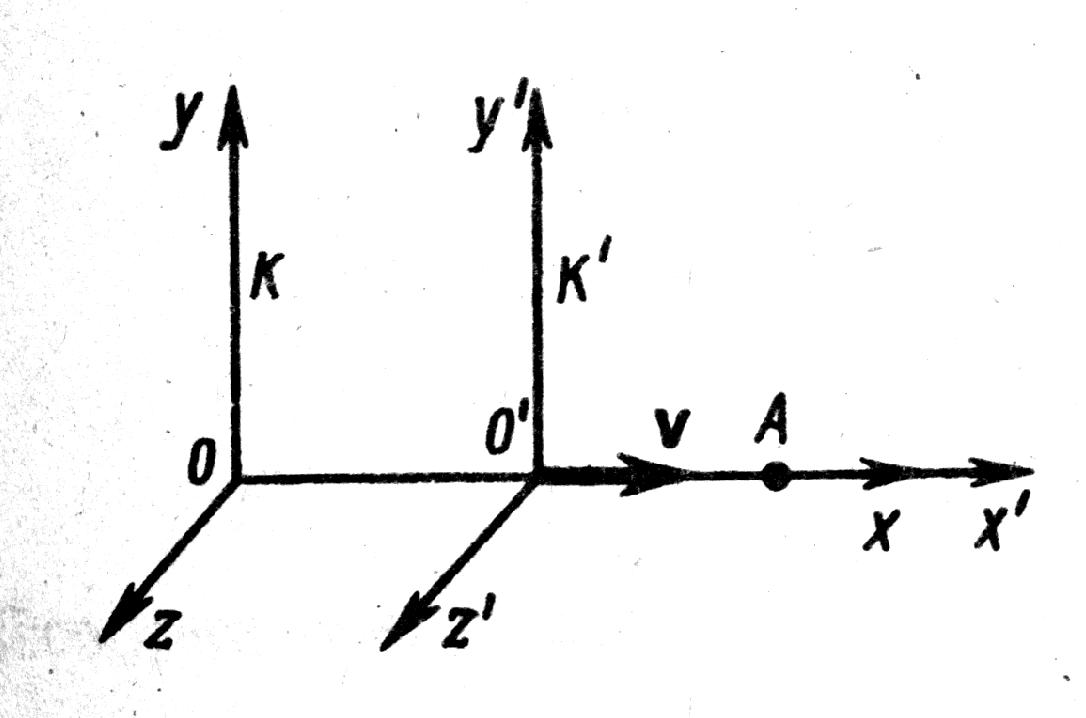 реобразования ЛоренцаРассмотрим две инерциальные системы: К(х,у,z) и К/(x/,y/,z/), движущуюся вдоль оси х со скоростью υ = const. В начальный момент t = t/ = 0, когда начало координат 0 совпадает с 0/, испускается световой импульс. В K x = ct, в K/ x/ = ct/, так как x/x, то t/t, то есть отсчет времени имеет относительный характер. Постулатам Эйнштейна удовлетворяют преобразование Лоренца. КK/K/K 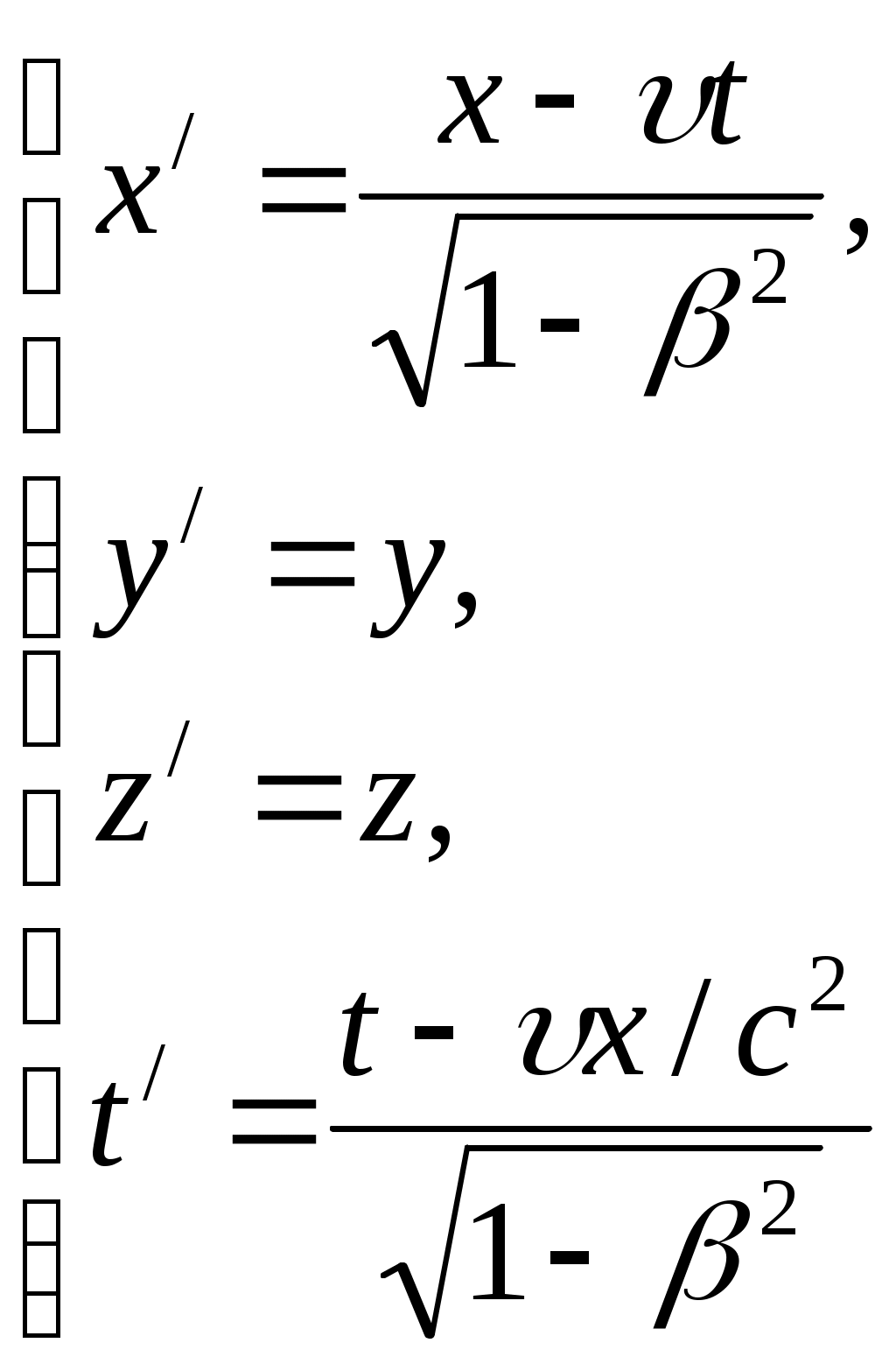 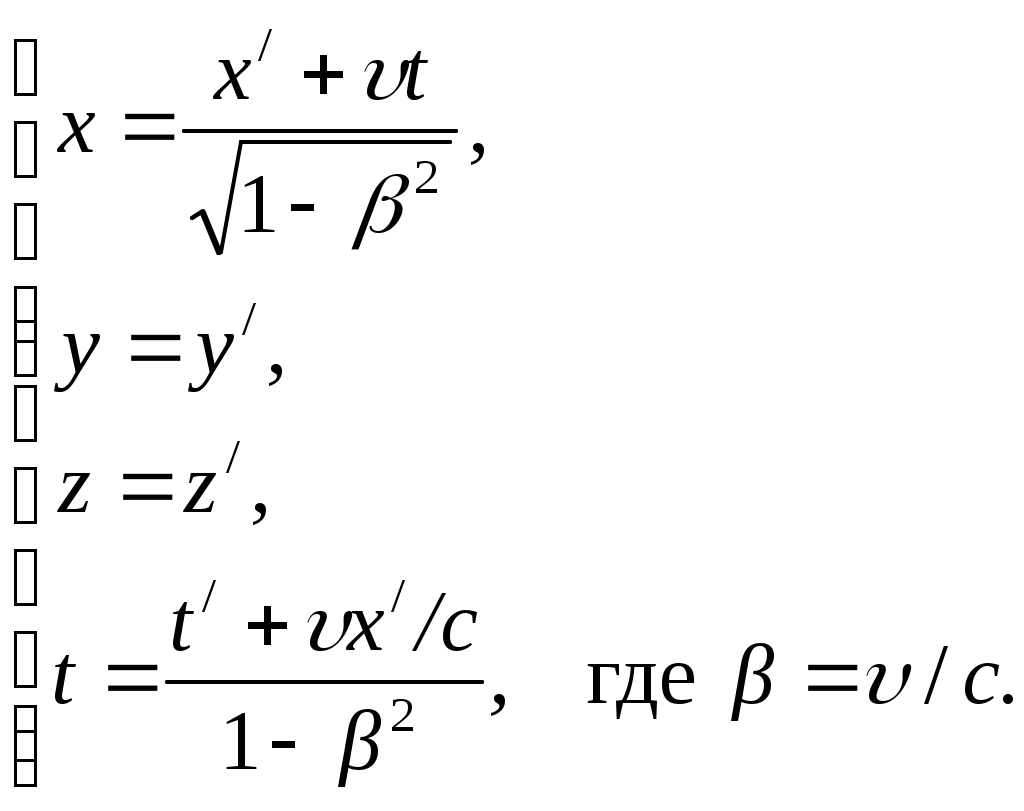 При малых υ преобразования Лоренца преобразуются в преобразования Галилея. Следствие из преобразований Лоренца. Одновременность событий в разных системах отсчета Пусть в системе К в точках с координатами х1 и х2 происходят одновременно два события t1= t2, то из преобразований Лоренца следует, что:  Таким образом, если х1 = х2 , то t1/ = t2/. Заметим, что  и при х1 = х2 х1/ = х2/. Итак, пространственно совпадающие и одновременные события являются пространственно совпадающими и одновременными во всех инерциальных системах отсчета. Если же события в системе К пространственно разобщены, (х1 х2), но одновременны, то в системе К/ эти события, оставаясь пространственно разобщенными, оказываются и неодновременными. Знак разности t1/ – t2/ зависит от величин (х1 – х2). Это значит, что в одних системах отсчета одно событие может предшествовать другому, а в других – наоборот. Длительность событий в разных системах отсчетаПусть в некоторой точке (с координатой х), покоящейся относительно К, происходит событие, длительность которого = t2 – t1. Длительность этого события в системе К/: / = t2/ – t1/ 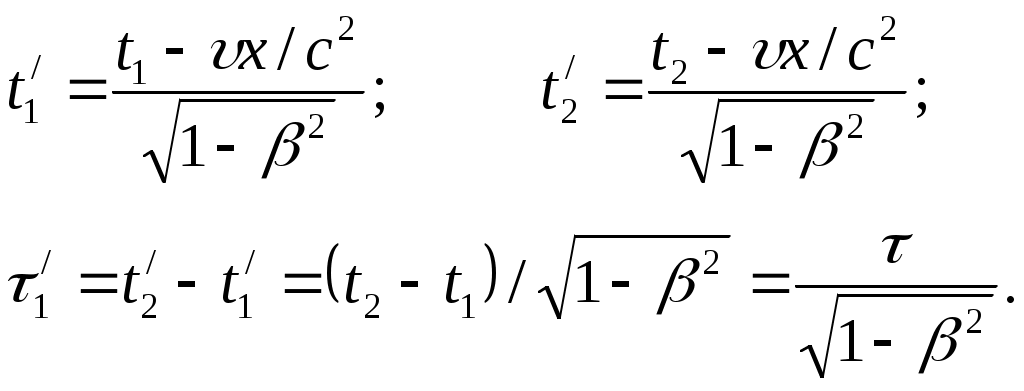 Отсюда видно, что /, т.е. длительность события, протекающего в некоторой точке, наименьшая в той инерциальной системе, относительно которой эта точка покоится. В движущейся системе отсчета процессы (часы) идут медленнее (относительно неподвижного наблюдателя). Релятивистский эффект замедления хода часов становится заметным, лишь при скоростях, близких к с. Это реальный эффект, наблюдаемый в опытах с -мезонами. 2,2.10-8 с – время жизни покоящегося мезона. Часы двигаются с ним. S = c 6,6 м. Они рождаются на высоте 30 км и долетают до Земли. Для земного наблюдателя  Длина тела в разных системах отсчетаРассмотрим стержень, расположенный вдоль оси х/, находящийся в системе К/, длиной  , где х2/ и х1/ – не изменяющиеся с течением времени координаты начала и конца стержня. В системе К в один и тот же момент времени t  . Тогда Длина стержня в системе, относительно которой он движется, меньше длины в системе, относительно которой он покоится. Это Лоренцево сокращение длины. Поперечные размеры   не изменяются.Пример с фотографией движущегося тела. Релятивистский закон сложения скоростей Путь К/ – инерциальная система, двигающаяся со скоростью υотносительно системы К. Возьмем в момент времени t/точку с координатами х/, y/, z/ или в К – t, x,y,z. Согласно преобразованию Лоренца: 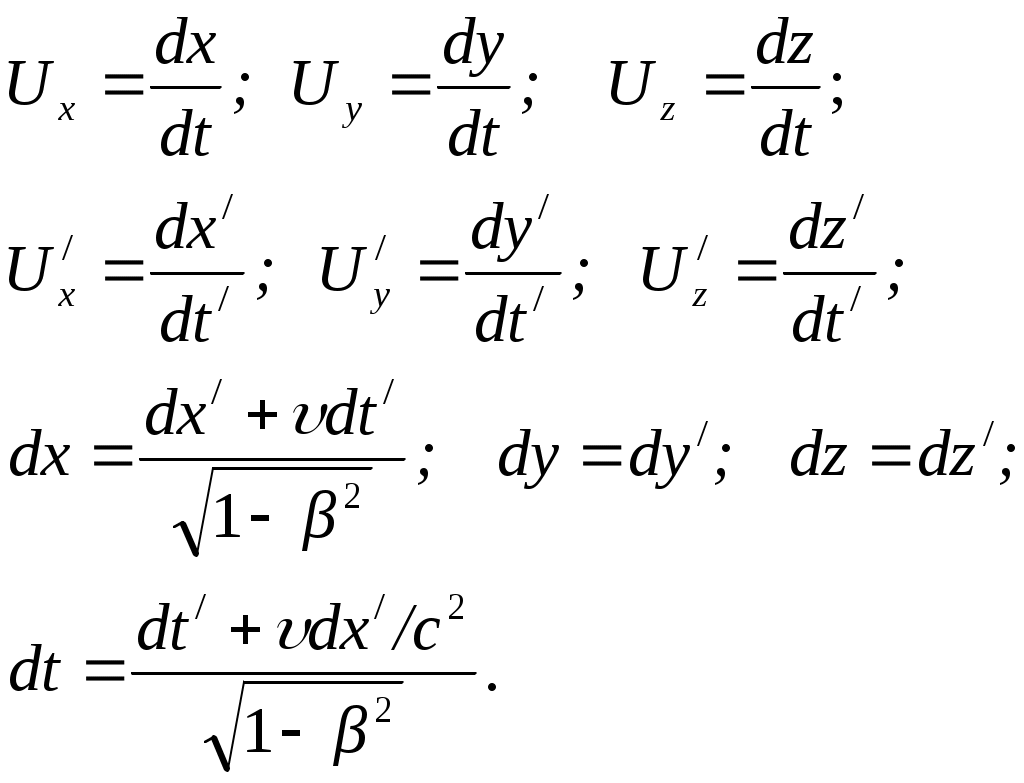 После преобразования получим релятивистский закон сложения скоростей специальной теории относительности: 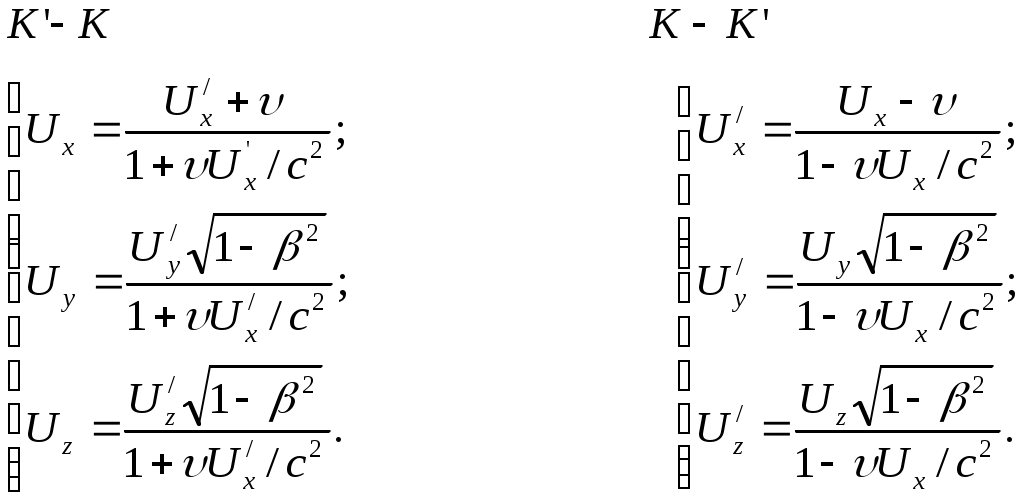 Если скорость Uсовпадает с Ux, а U/ с Uх/, то  Если υ и U<< c, то U = U/ +υ и U/= U-υ – совпадает с законом сложения скоростей в классической механике. Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна U/ = c; υ = υ. 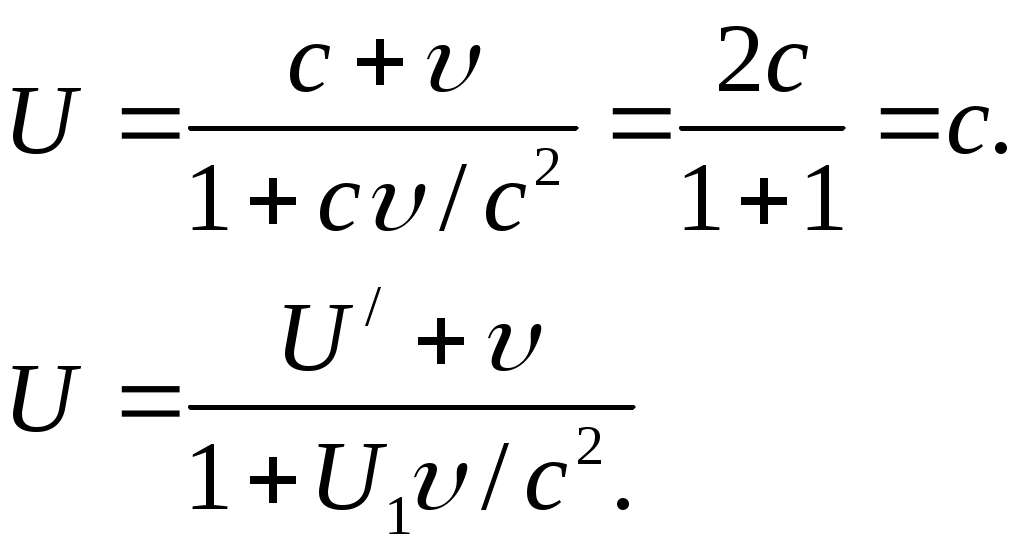 Таким образом, при сложении υ не может быть больше c в вакууме. Скорость света в среде υ = с/n, где n – абсолютный показатель преломления предельной величиной не является. Интервал между событиямиЕсли рассматривать воображаемое четырехмерное пространство – время, где три координаты пространственные, а четвертая – ct– тоже имеет размерность длины, то каждому событию в воображаемом пространстве можно сопоставить мировую точку. Квадрат расстояния между двумя точками в таком пространстве называется интервалом  Качественное различие между временем и пространством проявляется в том, что квадрат временной координаты и квадраты пространственных координат входят в выражение интервала с разными знаками.Об инвариантности Инвариантность – неизменность при переходе от одной инерциальной системы к другой. Инвариантны законы Ньютона по отношению к преобразованиям Галилея, но не инвариантны по отношению к преобразованиям Лоренца. Например, вытекающий из них закон сохранения импульса. Рассмотрим абсолютно неупругое центральное соударение двух одинаковых по массе частиц. Система К/ двигается со скоростьюυотносительно системы К вдоль осиx. В системе К/шары двигаются со скоростью υнавстречу друг другу. В этой системе импульс сохраняется и равен нулю до и после столкновения. С использованием преобразований Лоренца легко показать, что в системе К до столкновения p = 2mυ/(1+υ2/c2), а после соударения p = 2mυ. Таким образом, закон сохранения импульса не соблюдается. Выражение, обеспечивающее инвариантность закона сохранения импульса получается, если время t заменить на собственное время τ.   – перемещение в той системе, где измеряется  , а связано с частицами.Тогда закон Ньютона  - основной закон релятивистской динамики материальной точки справедлив.Трактовать импульс можно и как  , где m =  , m – релятивистская масса.Тогда инвариантная масса m0 называется массой покоя при υ<<c,   .Условия применения ньютоновской механики υ<<c. Классическая механика – механика макротел, движущихся с малыми скоростями (по сравнению с с). Закон взаимосвязи массы и энергииВажным результатом теории является универсальное соотношение между энергией тела и его массой:  - это универсальный закон.Разложив в ряд  Е0 = m0c2 – энергия покоя. Классическая механика считает, что при υ = 0, E0 = 0. Релятивистское выражение для кинетической энергии:  - для любых скоростей.При υ < Релятивистское соотношение между полной энергией и импульсом частицы   Энергия связи системы – работа, необходимая для разложения системы частиц на составные части:  m0i – масса покоя частицы, М0 – масса покоя системы. Это важно при ядерных реакциях и т.д. |