Физика_задачи. Физические основы механики
 Скачать 1.24 Mb. Скачать 1.24 Mb.
|
 ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИПредмет физики. Методы физического исследования: наблюдение, эксперимент, гипотеза теория. Роль физики в развитии техники, влияние техники на развитие физики. Связь физики с другими науками. Физические основы классической механики Пространство, время, движение. Механическое движение как простейшая форма движения материи. Представление о свойствах пространства и времени, лежащие в основе классической (ньютоновской) механики. Способы описания движения в механике. Системы отсчета. Элементы кинематики материальной точки: скорость и ускорение как производные радиус-вектора по времени, нормальное и тангенциальное ускорения. Принцип относительности Галилея. Преобразование координат и времени в классической механике. Кинематика поступательного и вращательного движения абсолютно твердого тела. Угловая скорость. Угловое и линейное ускорения. Связь векторов линейной и угловой скорости, линейного и углового ускорения. Динамические принципы механики . Масса. Импульс. Определение состояния частицы и системы частиц в классической механике. Основное уравнение динамики поступательного движения. Принцип причинности в классической механике. Силы. Виды сил. Консервативные силы. Поле как форма материи, осуществляющая взаимодействие между частицами вещества. Фундаментальные взаимодействия и их общая характеристика. Работа силы. Кинетическая энергия. Потенциальная энергия материальной точки в силовом консервативном поле. Динамика вращательного движения абсолютно твердого тела. Основное уравнение динамики вращательного движения. Момент импульса и момент силы относительно неподвижной оси вращения. Момент инерции тела. Кинетическая энергия вращающегося тела. Законы сохранения. Закон сохранения импульса и его связь с однородностью пространства. Кинетическая энергия механической системы и ее связь с работой внешних сил, приложенных к системе. Энергия как универсальная мера различных форм движения и взаимодействия. Закон сохранения механической энергии и его связь с однородностью времени. Закон превращения энергии как проявление вечности материи и ее движения. Закон сохранения момента импульса и его связь с изотропностью пространства. Колебания и волны. Общая характеристика колебательных движений. Гармонические колебания. Дифференциальное уравнение гармонических колебаний. Пружинный, физический и математический маятники. Энергия гармонических колебаний. Биение. Затухающие колебания. Апериодическое движение. Вынужденные колебания. Амплитуда, частота и фаза вынужденных колебаний. Резонанс. Распространение колебаний в упругой среде. Волновое уравнение. Продольные и поперечные волны и их характеристика. Фазовая скорость и дисперсия волн. Энергия волны. Принцип суперпозиции волн. Интерференция волн. Образование стоячих волн. Волновой пакет. Групповая скорость волн. Отражение волн от границы раздела двух сред. Элементы специальной (частной) теории относительности Принцип относительности Эйнштейна. Постулат об инвариантности скорости света. Преобразование Лоренца для координат и времени. Релятивистское изменение длины и промежутков времени. Пространственно–временной интервал. Релятивистский импульс, полная энергия частицы. Закон взаимосвязи массы и энергии. Критика философского релятивизма и энергетизма. Элементы квантовой механики и квантово- механической теории атомов Физические основы квантовой механики. Корпускулярно-волновой дуализм материи, его проявления и способы описания. Соотношение неопределенностей. Формула де Бройля. Границы применимости классической механики. Понятие о принципах дополнительности и соответствия. Определение состояния в квантовой механике. Волновая функция и ее статистический смысл. Стационарные состояния. Общее уравнение Шредингера для стационарных состояний. Основная задача квантовой механики и общая схема ее решения. Изображение механических величин операторами. Принцип причинности в квантовой механике. Критика идеалистического толкования принципов неопределенности и причинности. Квантование механических величин. Законы сохранения в квантовой механике. Квантово–механические задачи о движении микрочастиц Задача о движении свободной микрочастицы. Движение микрочастиц в потенциальных полях. Финитное и инфинитное движение. Микрочастица в одномерной “потенциальной яме” с прямоугольными непроницаемыми “стенками”. Сравнение квантово-механического и классического рассмотрений задач о движении микрочастиц. Элементы квантово–механической теории атомов Краткий очерк развития представлений о строении атома. Теория атома водорода по Бору. Постулаты Бора. Дискретность энергетических уровней в атомах. Задача о квантово–механических состояниях электрона в водородо-подобном ионе. Спин электрона. Принцип Паули. РАЗДЕЛ 1. МЕХАНИКА 1.1. Кинематика Методические указания 1. Прямая задача кинематики: по известному закону движения  определить характеристики движения (скорость, ускорение, траекторию). Задача решается путем дифференцирования уравнения, выражающего закон движения, а также с помощью формул связи одних характеристик движение с другими. определить характеристики движения (скорость, ускорение, траекторию). Задача решается путем дифференцирования уравнения, выражающего закон движения, а также с помощью формул связи одних характеристик движение с другими.2. Обратная задача: по известным характеристикам движения и начальным условиям найти закон движения. Задача решается интегрированием характеристик движения. Для нахождения траектории движения, т.е. для установления связи между координатами у = f(х), следует исключить время из системы уравнений, выражающих законы движения вдоль координатных осей. При решении задач необходимо:
радиус-вектора 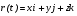 , ,где  - единичные векторы вдоль координатных осей X, Y и Z; - единичные векторы вдоль координатных осей X, Y и Z;скорости 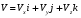 , ,  где 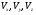 - проекции вектора скорости на оси координат; - проекции вектора скорости на оси координат;ускорения 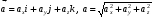 , ,где ах, ау, аz - проекции вектора ускорения на оси координат;
S = RΔφ (Δφ - угол поворота);
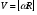 , или , или  ; ;
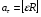 , или , или 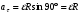 ; ;
 . .Основные формулы и примеры решения задач Таблица 1.1 Сопоставление поступательного и вращательного движений
Пример 1.1 Два тела движутся в одном направлении вдоль оси X согласно уравнениям 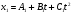 и и  , где А1 = 20 м, А2 = 2 м, В1 = 8 м/с, В2 = 2 м/с, С1 = – 4 м/с2, С2 = 0,5 м/с2. , где А1 = 20 м, А2 = 2 м, В1 = 8 м/с, В2 = 2 м/с, С1 = – 4 м/с2, С2 = 0,5 м/с2.В какой момент времени скорости этих тел будут равны? Найти скорости V1, V2 и ускорения а1, а2 в этот момент. Решение По определению скорость есть первая производная от координаты по времени, а ускорение, соответственно, вторая производная. Найдем выражения для скоростей тел  , ,  и для ускорений  , , 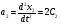 . .При V1 = V2 имеем B1 +2C1t = B2+2C2t . Решая это уравнение относительно t, найдем  . .Подставив найденное значение t в выражение для скорости, получим V1 = V2 = 8 – 8 (2/3) = 2,7 м/с . Ускорения a1 и а2 от времени не зависят и равны соответственно а1 = – 8 м/с2, а2 = 1 м/с2 . Это означает, что первое тело тормозится, а второе разгоняется. Пример 1.2 O X Vx Vy V Sx Y V С башни высотой Н = 25 м горизонтально брошен камень с начальной скоростью Vо = 15 м/с. Найти: 1) время падения; 2) расстояние от основания башни до места падения; 3) скорость камня в момент удара о землю; 4) угол между вектором мгновенной скорости камня и горизонтом через одну секунду после начала движения. Решение Движение камня криволинейное. Вектор скорости в любой момент времени касателен к траектории и может быть разложен на cоставляющие вдоль координатных осей: Vx = Vо = соnst (вдоль оси X движение равномерное) и Vу =gt (движение вдоль оси У равноускоренное). Время падения tпад может быть найдено из закона движения вдоль оси У: у = Н = gt2/2. Следовательно, 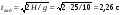 . .Расстояние от основания башни до места падения камня Sx= Vо tпад =15 ∙ 2,26 = 33,9м. Модуль вектора скорости камня  в момент падения на землю находится как сумма скоростей в момент падения на землю находится как сумма скоростей 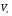 и и  , а ее модуль по теореме Пифагора: , а ее модуль по теореме Пифагора: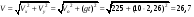 м/с. м/с.В любой момент времени угол 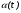 между вектором скорости между вектором скорости  и осью X может быть найден из отношения составляющих и осью X может быть найден из отношения составляющих 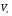 и и  : : . .Следовательно, для момента времени t = 1с, имеем = arctg(10/15) = 33°36'. Заметим, что время падения зависит только от высоты башни, а все остальные величины (Sx,V,) зависят ещё и от начальной скорости бросания 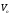 . .Пример 1.3 Диск вращается равноускоренно. Найти угол , который составляет вектор 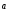 полного ускорения любой точки диска с радиусом в тот момент, когда диск совершает первые два оборота. полного ускорения любой точки диска с радиусом в тот момент, когда диск совершает первые два оборота. Решение Разложив вектор 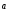 в произвольной точке М диска на тангенциальное в произвольной точке М диска на тангенциальное  и нормальное и нормальное 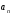 ускорения, определим тангенс искомого угла:tg = aτ/an. ускорения, определим тангенс искомого угла:tg = aτ/an.Тангенциальное  и нормальное и нормальное 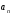 ускорения определяют быстроту изменения скорости по модулю и по направлению соответственно, и являются проекциями вектора ускорения определяют быстроту изменения скорости по модулю и по направлению соответственно, и являются проекциями вектора 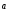 полного ускорения на касательную к траектории и на нормаль (перпендикуляр) к ней. полного ускорения на касательную к траектории и на нормаль (перпендикуляр) к ней.aτ a α М О an Перейдем от а и аn к угловым величинам и , тогда 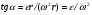 . Для нахождения правой части этого равенства воспользуемся формулами равноускоренного движения: φ=ω0t+εt2/2, ω=ω0+εt. . Для нахождения правой части этого равенства воспользуемся формулами равноускоренного движения: φ=ω0t+εt2/2, ω=ω0+εt.Исключив из них время, получим  . Учитывая далее, что φо = 0 и φ = 2πN, получим . Учитывая далее, что φо = 0 и φ = 2πN, получим 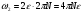 и, следовательно, и, следовательно, tg =1/(4πN)=0,040; = 2,3°. Заметим, что угол не зависит от выбора точки М диска и полностью определяется углом φ поворота диска. При заданном угле поворота угол не зависит от промежутка времени, в течение которого произошел этот поворот. При этом в начальный момент времени, N = 0, tg = , = π/2, т.е. вектор 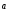 направлен по касательной к окружности в точке М. Наоборот, при возрастании оборотов N угол убывает, стремясь к нулю при N → , а вектор направлен по касательной к окружности в точке М. Наоборот, при возрастании оборотов N угол убывает, стремясь к нулю при N → , а вектор 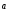 направлен к центру кривизны траектории. направлен к центру кривизны траектории.1.2 Динамика поступательного и вращательного движения Основу динамики составляют три закона Ньютона. Первый закон Ньютона (закон инерции): в инерциальных системах отсчёта (ИСО) всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока на него не подействуют другие тела и не выведут его из этого состояния. Смысл первого закона Ньютона заключается в том, что второй и третий законы справедливы только в ИСО. Свойство тел сохранять свою скорость неизменной называется инертностью. Мерой инертности при поступательном движении является масса тела m, а при вращательном движении - момент инерции тела I. Любое тело можно представить как совокупность материальных точек. Сумма моментов инерции этих точек относительно оси вращения, будет определять момент инерции тела в целом. В табл.1.2 приведены формулы расчета моментов инерции тел различной геометрической формы. Момент инерции I тел относительно любой оси, не проходящей через центр масс, может быть рассчитан по теореме Штейнера: I = Iо + md 2, где Iо - момент инерции тела относительно центра масс, d - кратчайшее расстояние от центра масс до рассматриваемой оси вращения. Второй закон Ньютона (закон силы) устанавливает, как изменяется механическое движение тела под действием приложенных сил. При взаимодействии тел изменяются динамические характеристики тел:  где импульс 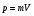 ; ;момент импульса 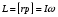 ; ;кинетическая энергия поступательного движения Кп = mV 2 / 2; кинетическая энергия вращательного движения Квр = I2 / 2. Таблица 1.2 Моменты инерции некоторых тел правильной геометрической формы
Третий закон Ньютона (закон равенства действия и противодействия): силы действия и противодействия равны по величине, противоположны по направлению и приложены к разным телам. Эти силы всегда действуют вдоль прямой, соединяющей взаимодействующие тела, и являются силами одной природы. В таблице 1.3 представлены формулы, выражающие законы Ньютона для поступательного и вращательного движений. Таблица 1.3 Сопоставление поступательного и вращательного движений
Методические указания и примеры решения задач по динамике 1. Сделать рисунок и указать на нем все силы, действующие на тело (или на тела системы). 2. Выбрать систему отсчета, одна из осей которой должна быть направлена по направлению движения. 3. Указать направление скорости движения тел и их расположение в начальном и конечном состояниях. 4. Записать в векторной форме уравнения движения тел, т.е. основной закон динамики (второй закон Ньютона). 5. Спроецировать эти уравнения на оси координат и получить систему уравнений в скалярной форме. 6. Дополнить при необходимости систему полученных уравнений кинематическими уравнениями. 7. Решив полученную систему уравнений, определить искомые величины. Пример 1.4 Закон движения материальной точки массой m = 0,1 кг задан в виде х = 8t2 + 3t + 1, у = 5t - 7, где х и у - в метрах, время t- в секундах. Определить проекции вектора силы на оси координат X, Y и модуль силы, действующей на материальную точку. Решение Движение точки происходит в плоскости ХОУ. Запишем основное уравнение динамики в проекциях на оси координат: Fх = mах = m 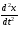 , , Fу = mау = m  . .Модуль силыF =  . . Проведя расчеты, найдем: ах =  = 16(м/с2); = 16(м/с2); ау =  = 0;Fх= 0,1 • 16 = 1,6 Н;FУ= 0; F =1,6 Н. = 0;Fх= 0,1 • 16 = 1,6 Н;FУ= 0; F =1,6 Н.Пример 1.5 Какую силу надо приложить для подъема тела массой 50 кг по наклонной плоскости с углом наклона φ= 60°, если коэффициент трения тела о плоскость = 0,2? Решение Y X N F 0 Fтр φ mg Полагая, что движение тела вдоль наклонной плоскости является равномерным и прямолинейным (ускорение а = 0), составим уравнение движения тела:  Направление сил, действующих на тело, показано на рисунке. В проекциях на координатные оси X и У это векторное уравнение запишется в виде двух скалярных уравнений: Решив эту систему с учетом формулы для силы трения Fтр = N, получим F=mg(sinφ + соsφ) = 50∙10[(  ) / 2+0,2 (1/2)]= 475 Н. ) / 2+0,2 (1/2)]= 475 Н. Из полученного решения видно, что при неизменном значении коэффициента трения, сила тяги тем больше, чем больше угол наклона плоскости. Пример 1.6 На тело массой m = 2 кг в течение времени t = 10 с действует сила F1 = 50 Н. Коэффициент трения тела о плоскость = 0,15. Найти приращение скорости и импульса тела за это время. Решение Согласно основному уравнению динамики в импульсной форме: 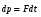 , где , где 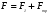 . Интегрируя обе части этого уравнения, получим приращение импульса за время t: . Интегрируя обе части этого уравнения, получим приращение импульса за время t: , или , или 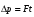 при при  . .Эта формула представляет собой математическое выражение теоремы об изменении импульса. Проецируя вектор  на направление движения, вычислим результирующую силу на направление движения, вычислим результирующую силу = 50 – 0,15∙2∙10 = 47Н. = 50 – 0,15∙2∙10 = 47Н. Подставим численные значения Fи t в формулу для приращения импульса: р=47∙10=470 Нс=470 кг∙м/с. Приращение скорости определим из следующего соотношения: V =   = 235 м/с. = 235 м/с.Пример 1.7 Диск массой m = 10 кг и радиусом R = 20 см вращается вокруг горизонтальной оси, проходящей через его центр. Уравнение вращения диска имеет вид: φ(t) = Вt2 – Сt3 ; В = 4 рад/c2, С = 1 рад/с3. Найти закон изменения момента сил, действующих на диск. Определить величину момента сил  в момент времени t = 2 с. в момент времени t = 2 с.Решение Воспользуемся основным законом динамики вращательного движения 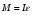 , где угловое ускорение может быть найдено дифференцированием уравнения вращения: = , где угловое ускорение может быть найдено дифференцированием уравнения вращения: = = 2В – 6Сt = 8 – 6t. = 2В – 6Сt = 8 – 6t.С учетом того, что момент инерции диска I= mR2 / 2, получим искомый закон изменения момента сил: М(t) =(1/2)mR2(8 - 6t) = (1/2) 10 ∙ 0,04 ∙ (8 –6t) = 1,6 – 1,2t. Отсюда следует, что зависимость М(t) – линейная. Для момента времени t = 2 с, величина момента сил М = 1,6 – 1,2 ∙ 2 = – 0,8Н∙м. Задачи
 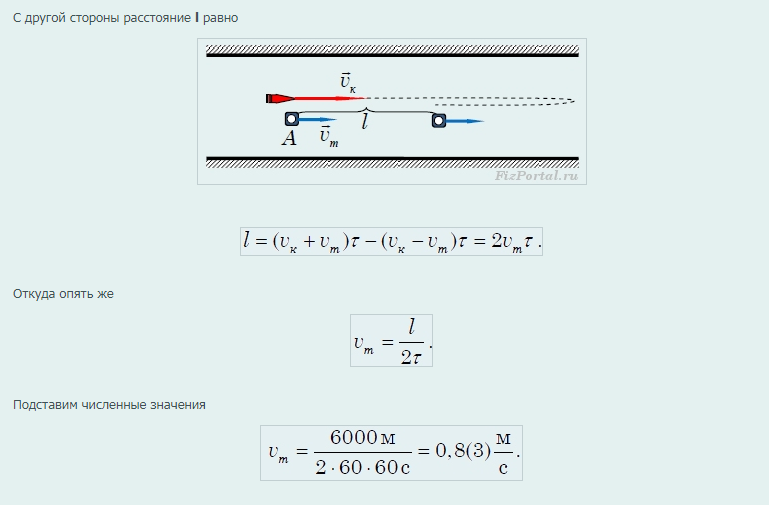
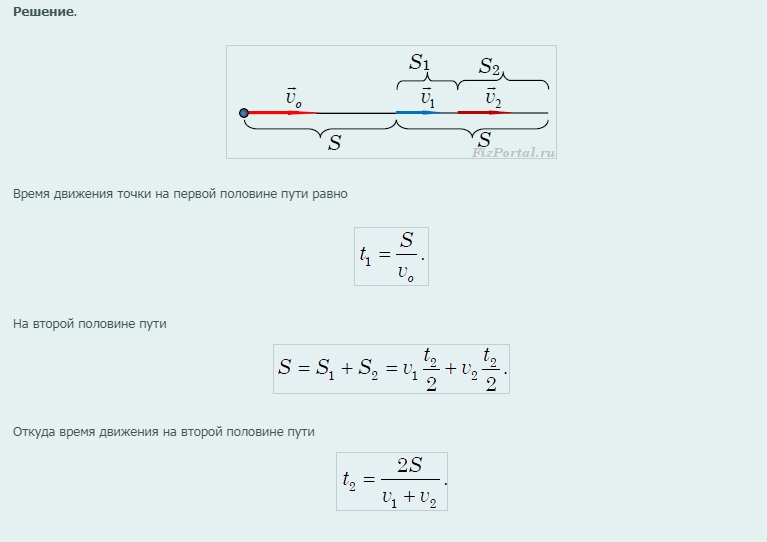 
 
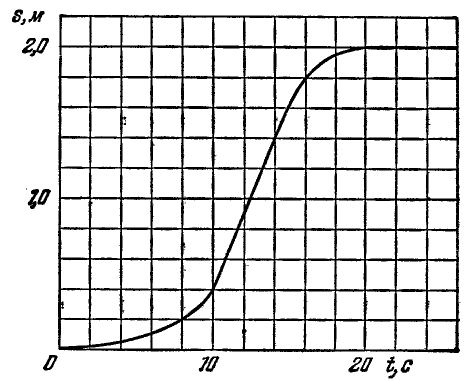 Рисунок 1.1 

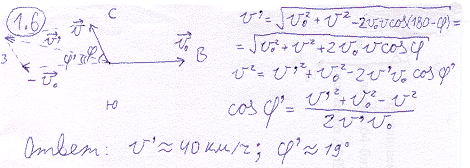

Решение на картинке ниже, сама картинка мать ее где? 
 рис. 1.23 рис. 1.23 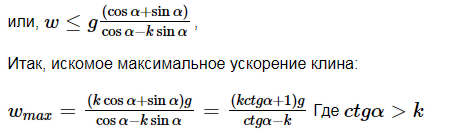
 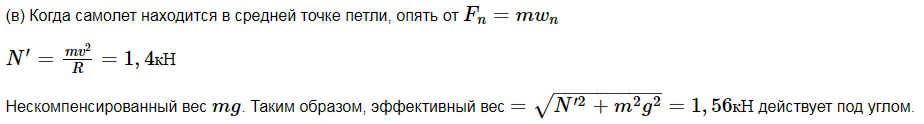
 
Решение на картинке ниже  | ||||||||||||||||||||||||||||||||||||||||||

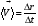 не равна средней путевой скорости <V> = ΔS/Δt – (
не равна средней путевой скорости <V> = ΔS/Δt – (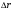 - вектор перемещения; ΔS– путь, пройденный за время Δt);
- вектор перемещения; ΔS– путь, пройденный за время Δt); - вектор линейного перемещения за время Δt
- вектор линейного перемещения за время Δt - вектор углового перемещения за время Δt
- вектор углового перемещения за время Δt

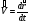
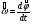
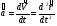 ;
; 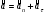 ;
; 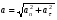 , где
, где  и
и 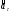 - нормальная и тангенциальная
- нормальная и тангенциальная
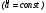
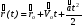 ,
, и
и  - начальные радиус- вектор и скорость
- начальные радиус- вектор и скорость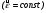
 ,
, и
и  - начальные угловое положение и угловая скорость
- начальные угловое положение и угловая скорость

 при m = const,
при m = const,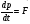
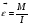 при I = const,
при I = const,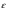 -
- 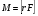 (
(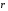 – радиус-вектор силы
– радиус-вектор силы 

