Физика пласта_Курс лекций. Физические свойства горных пород коллекторов нефти и газа

• Название: Физические свойства горных пород коллекторов нефти и газа
• Дата: 16.03.2022
• Размер: 2.6 Mb.
• Имя файла: Физика пласта_Курс лекций.docx
• Тип: Документы; #399443
• страница: 3 из 9

Методы определения удельной поверхности горных пород
Кроме упомянутых способов определения удельной поверхности пород по их гранулометрическому составу, по величине пористости и проницаемости, существуют следующие способы оценки этого параметра пористых сред: фильтрационный, основанный на измерении сопротивления течению через пористое тело разреженного воздуха; адсорбционные, а также метод меченых атомов. Методы определения удельной поверхности пористых сред, основанные на использовании пуазейлевского режима течения воздуха сквозь объект исследования (т. е. основанные на использовании формул типа (1.14)), применимы только для приближенной оценки поверхности грубозернистых однородных сред, ширина пор в которых намного больше длины свободного пробега молекул воздуха, так что не нужно учитывать скольжения газа по стенкам пор. Движение газа в мелкодисперсной пористой среде существенно облегчается при скольжении молекул по стенкам пор, и сопротивление среды с высокой удельной поверхностью прохождению через нее газов иногда существенно меньше по сравнению с подсчитанными по формулам типа (1.14), не учитывающим скольжения газа по стенкам. Поэтому в данном случае можно использовать метод, основанный на измерении сопротивления течению через пористое тело разреженного воздуха при кнудсеновском режиме, имеющим скорее диффузивный характер. Кнудсеновский режим наступает, когда максимальные просветы пор становятся меньше длины свободного пробега молекул газа и соударения молекул между собой становятся редкими (по сравнению с ударами о стенки пор). Зависимость молярной скорости течения газа от удельной поверхности и других параметров выражается равенством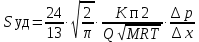
,
где S_уд - удельная поверхность образца в м²/м³;

Q- число киломолей воздуха, протекающих через 1 м² сечения пористой среды толщиной ∆х(в м) за 1 с при перепаде давления ∆р(в Па);

М- относительная молекулярная масса воздуха в кг/кмоль;

R- универсальная газовая постоянная в Дж/кмоль·град;

Т- температура опыта в °С.

Для определения удельной поверхности пористых тел по результатам измерения кнудсеновского режима фильтрации сконструированы специальные приборы.

Горные породы, слагающие пласт, заполнены жидкой средой - водой и нефтью. Удельная поверхность (например, глин и некоторых других пород) под действием водной среды может изменяться, и "сухие" способы ее измерения не всегда соответствуют действительным условиям залегания пород в естественных условиях. Удельную поверхность пористых сред в водной среде обычно определяют методом адсорбции красителей или методом поверхностного обмера при помощи радиоактивных индикаторов. Площадь поверхности минералов Sпри этом рассчитывают по числу молекул радиоактивного индикатора, поглощенных пористой средой, и по площади, приходящейся на один атом данного радиоактивного вещества на поверхности кристалла: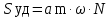

,

где а_m- число грамм-атомов вещества, связанного с 1 г твердой фазы;

ω - площадь, приходящаяся на один атом данного вещества на поверхности кристалла (величина, известная для многих веществ);

N- число Авогадро.

Количество радиоактивного иона, поглощенного веществом при его погружении в раствор, определяется по убыли активного фильтрата раствора вследствие поглощения меченого атома твердой фазой. Особое место по точности занимает адсорбционный метод вследствие того, что поверхность пористой среды прощупывается такими малыми объектами, как молекулы адсорбируемого вещества, выстилая ими поверхность пористой среды. По количеству адсорбированного вещества (т. е. по числу его молекул) и площади, приходящейся на один атом данного вещества, вычисляется удельная поверхность пористой среды.

При адсорбционных методах исследования удельной поверхности пористых сред необходимы сложная аппаратура, высококвалифицированные исполнители. Поэтому в лабораториях физики нефтяного пласта удельная поверхность пород обычно оценивается фильтрационными методами.
1.6. Проницаемость горных пород
Проницаемость - важнейший параметр, характеризующий проводимость коллектора, т. е. способность пород пласта пропускать к забоям скважин нефть и газ при наличии перепада между пластовым и забойным давлениями.

Абсолютно непроницаемых тел в природе нет. Однако при существующих в нефтяных пластах сравнительно небольших перепадах давлений многие породы из-за малых размеров пор в них оказываются практически мало или совсем непроницаемыми для жидкостей и газов (глины, сланцы и др.).

Большая часть осадочных пород обладает той или иной проницаемостью. Поровое пространство этих пород, кроме субкапиллярных пор, слагается также порами большего размера. По экспериментальным данным диаметры подавляющей части пор нефтесодержащих коллекторов больше 1 мкм.

В процессе эксплуатации нефтяных и газовых месторождений возможна различная фильтрация в пористой среде жидкостей и газов или их смесей - совместное движение нефти, воды и газа или воды и нефти, нефти и газа или только нефти или газа. При этом проницаемость одной и той же пористой среды для данной фазы в зависимости от количественного и качественного состава фаз в ней будет различной. Поэтому для характеристики проницаемости пород нефтесодержащих пластов введены понятия абсолютной, фазовой и относительной проницаемости.

Для характеристики физических свойств пород используется абсолютная проницаемость. Под абсолютной принято понимать проницаемость пористой среды, которая определена при наличии в ней лишь одной какой либо фазы, химически инертной по отношению к породе. Для ее оценки обычно используется воздух или газ, так как установлено, что при движении жидкостей в пористой среде на ее проницаемость влияют физико-химические свойства жидкостей.

Фазовой называется проницаемость пород для данного газа или жидкости при наличии или движении в порах многофазных систем. Величина ее зависит не только от физических свойств пород, но также от степени насыщенности порового пространства жидкостями или газом и от их физико-химических свойств.

Относительной проницаемостью пористой среды называется отношение фазовой проницаемости этой среды к абсолютной.

Для оценки проницаемости горных пород обычно пользуются линейным законом фильтрации Дарси, по которому скорость фильтрации жидкости в пористой среде пропорциональна градиенту давления и обратно пропорциональна динамической вязкости: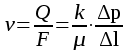

, (1.14)

где v – скорость линейной фильтрации;

Q – объемный расход жидкости в единицу времени;

µ – динамическая вязкость жидкости;

F – площадь фильтрации;

Δр – перепад давления;

l – длина пористой среды.

В этом уравнении способность породы пропускать жидкости и газы характеризуется коэффициентом пропорциональности k, который в нефтепромысловой практике принято называть коэффициентом проницаемости (k → k_пр)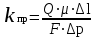

(1.15)

Размерность коэффициента проницаемости вытекает из уравнения (1.15):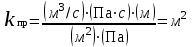


В системе СИ коэффициент проницаемости измеряется в м², в СГС в см², в системе нефтепромысловой геологии (НПГ) в Д (дарси), то есть для разных систем единиц измерения величина его характеризует площадь (табл. 1.2).

Физический смысл размерности коэффициента проницаемости – это величина площади сечения каналов пористой среды горной породы, по которым происходит фильтрация флюидов.

Таблица 1.2

Размерность параметров уравнения Дарси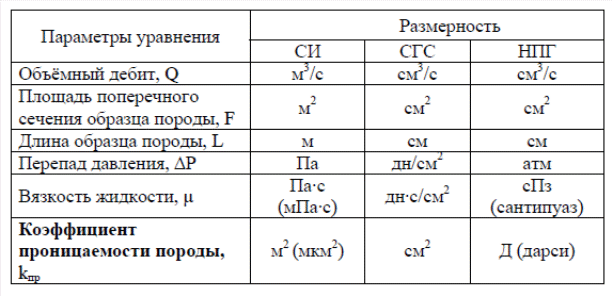



Проницаемостью в 1 м² называется проницаемость пористой среды при фильтрации, через образец которой площадью 1 м² под действием градиента давления 1 Па/м расход жидкости вязкостью 1 Па·с составляет 1 м³/с.

Пористая среда имеет проницаемость 1 Д, если при однофазной фильтрации жидкости вязкостью в 1 сПз при ламинарном режиме фильтрации через сечение образца площадью 1 см² и перепаде давления 1 атм расход жидкости на 1 см длины породы составляет 1 см³/с.

Выражение вязкости в сПз имеет и физический смысл. Вязкость воды при 20 ^оС равна 1,005 сПз (≈ 1сПз) и величину k_пр= 1,02 см²/10⁸ назвали Дарси:
1 Д = 1,02·10^-8 см² = 1,02·10^-12 м² = 1,02 мкм² ≈ 1 мкм².
Приведённые выше уравнения справедливы для условий движения слабосжимаемой жидкости при линейно-направленном потоке. Газ - сжимаемая система и при уменьшении давления по длине образца объёмный расход газа непостоянный.

Поэтому при расчёте коэффициента проницаемости по газу следует учитывать средний расход газа в условиях образца (рис. 1.11), приведенный к среднему давлению и средней температуре образца, используя закон Бойля-Мариотта: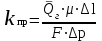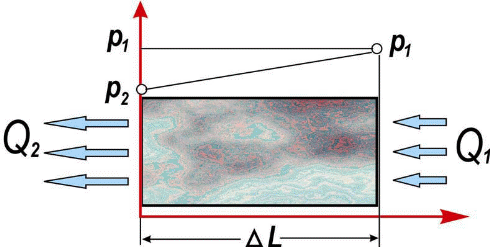



Рис. 1.11. Фильтрация газов
Если расширение газа при линейном прохождении его через образец происходит изотермически, следует учитывать средний объёмный расход (V_ср):

При Т = const, P·V = const, (1.16)
V_cр·P_ср = V_о·P_о = V₁·P₁ = V₂·P₂, (1.17)
P_ср = (P₁ + P₂)/2, (1.18)
V_cр = V_о·P_о/P_ср = 2·V_о·P_о/(P₁ + P₂). (1.19)
Средний объёмный расход газа будет пропорционален изменению линейной скорости фильтрации объёма газа (V_ср) за время (продолжительность, τ) прохождения газа через породу: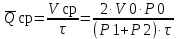

(1.20)
Уравнение для количественной оценки коэффициента проницаемости горных пород при линейной фильтрации газа запишется с учетом выражений (1.15) и (1.20):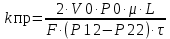
(1.21)

где Q_ср - объемный расход газа, м³/с;

V₀ - объемный расход газа при атмосферном давлении, м³;

Р₀ - атмосферное давление, Па;

Р₁ - давление на входе образца, Па;

Р₂ - давление на выходе образца, Па;

F - площадь фильтрации, м²;

µ - динамическая вязкость газа, Па·с;

τ - время фильтрации;

L – длина образца.

Уравнения (1.15, 1.21) применимы при описании линейного, плоскопараллельного потока фильтрации жидкости и газа через породу.
Радиальная фильтрация пластовых флюидов
Как уже отмечалось, формула (1.15) соответствует закону Дарси при линейном (плоскопараллельном) потоке. Иногда необходимо определять проницаемость образцов при радиальной фильтрации жидкости и газа, т. е. как бы при воспроизведении условий притока их в скважину. В этом случае образец породы имеет вид цилиндрического кольца с осевым отверстием - скважиной (рис. 1.12).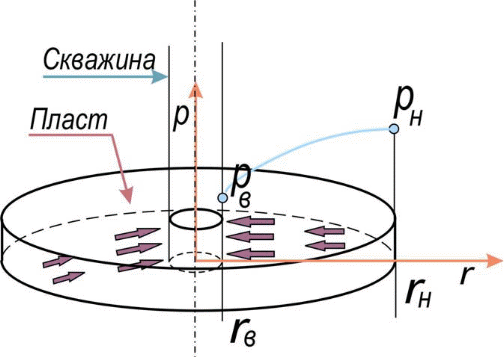


Рис. 1.12. Радиальная фильтрация флюидов
Фильтрация жидкости или газа в нем происходит в радиальном направлении от наружной поверхности к внутренней. Тогда проницаемость пород по данным опыта определяют по следующим формулам.

При фильтрации жидкости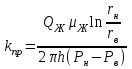

. (1.22)

При фильтрации газа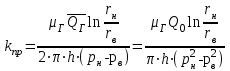

. (1.23)

где μ_ж, μ_г - вязкость жидкости и газа;

Q_ж - расход жидкости;

r_н и r_в - наружный и внутренний (радиус скважины) радиусы контуров

фильтрации;

Q_г, Q₀ - расход газа при среднем и атмосферном давлениях в образце;

Р_н, Р_в - давления у наружной и внутренней поверхностей кольцевого образца;

h - высота цилиндра.
Классификация проницаемых пород
Для нефтяных месторождений по величине коэффициента проницаемости (мкм²) выделяют 5 классов коллекторов:

1. Очень хорошо проницаемые (k_пр > 1).

2. Хорошо проницаемые (k_пр ≈ 0,1–1).

3. Средне проницаемые (k_пр ≈ 0,01–0,1).

4. Слабопроницаемые (k_пр ≈ 0,001–0,01).

5. Плохопроницаемые (k_пр < 0,001).

Классификация коллекторов газовых месторождений по величине коэффициента проницаемости включает 1–4 классы. По характеру проницаемости (классификация Г.И. Теодоровича) различают следующие виды коллекторов: равномерно проницаемые; неравномерно проницаемые; трещинные.

В реальных условиях редко встречаются пласты, однородные по проницаемости на всём протяжении. Нефтяной пласт неоднороден и состоит из продуктивных пропластков разной проницаемости. Коллекторы нефти и газа меняются по минералогическому составу, физическим свойствам по вертикали и горизонтали, по направлениям напластования пород. Линзы песчаников, пропластки песка иногда без каких–либо закономерностей переходят в глинистые породы. Поэтому коэффициент средней проницаемости продуктивного пласта ( 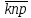) оценивается с учётом проницаемости пропластков и направления фильтрации.
1.7. Оценка проницаемости продуктивного пласта
Породы, залегающие в недрах земли, находятся под влиянием горного давления, которое обусловлено весом пород, тектоническими силами, напором подземных вод и газов, силами тектонического движения земной коры, термическими напряжениями, возникающими под влиянием тепла земных недр, пластовым давлением. В результате воздействия на породу комплекса упомянутых сил элемент породы, выделенный из массива, может находиться в условиях сложного напряжённого состояния. Оно характеризуется тем, что результирующие векторы напряжений, действующие на грани, не являются перпендикулярами к его граням. Компоненты напряжений зависят от ориентации выделенного элементарного объёма породы в пространстве.

Элементарный объём – это физическое свойство, тот представительный объём, который характеризует свойство объёма. Процессы, в массивах пород идут по осям, то есть по векторам напластования. А, следовательно, суммарные макроскопические свойства массивов пород: теплопроводность, электрические свойства и другие, включая и коэффициенты проницаемости – величины тензорные, зависящие от направления поля действия и степени ориентации минеральных частиц.

1. Рассмотрим случай линейно-горизонтальной фильтрации жидкости, направленной параллельно напластованию в пласте, состоящем из нескольких изолированных слоёв или пропластков пористой среды, разделенных между собой бесконечно тонкими непроницаемыми перегородками различной мощности и проницаемости (рис. 1.13).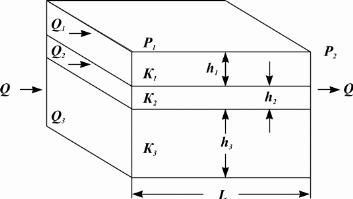

Рис. 1.13. Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости
Средняя величина коэффициента проницаемости пласта будет оцениваться с учётом мощности продуктивных пропластков, через которые идёт фильтрация и вида её направления. Для данного случая она идёт параллельно напластованию: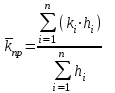


где 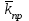– средняя проницаемость пласта;

k_i – проницаемость i-го пропластка;

h_i – мощность (высота) i-го пропластка.
2. Рассмотрим случай горизонтально-линейной фильтрации жидкости, направленной перпендикулярно напластованию, через пласт, имеющий несколько параллельно-последовательно расположенных изолированных зон пористой среды различной проницаемости (рис. 1.14).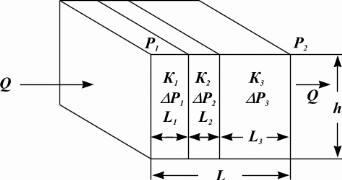


Рис. 1.14. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости
Средняя величина коэффициента проницаемости такого пласта рассчитывается с учётом протяженности (длины) фильтрации флюидов и её направленности: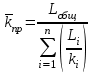



где 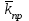– средняя проницаемость пласта;

k_i – проницаемость пропластков;

L_i – длина i-го пропластка;

L_общ – общая длина пласта;

L_общ =  L_i.
3. Рассмотрим случай радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.15).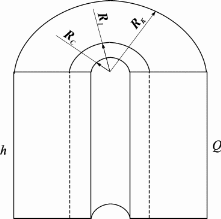

Рис. 1.15. Радиальная фильтрация через пласт, имеющий несколько концентрически расположенных зон различной проницаемости
Средняя величина коэффициента проницаемости для пласта оценивается с учетом радиуса контура радиальной фильтрации флюидов через продуктивные пропластки по выражению: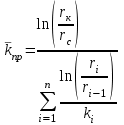


где 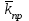– средняя проницаемость пласта, мД;