Физика пласта_Курс лекций. Физические свойства горных пород коллекторов нефти и газа
 Скачать 2.6 Mb. Скачать 2.6 Mb.
|
|
3.2. Аддитивный подход к расчету физико-химических свойств углеводородных газов Как отмечалось выше, в нефтяной газ при нормальных и стандартных условиях входят углеводороды от С1 до С4: метан, этан, пропан, изобутан и н-бутан. С точки зрения строения все они линейно построены, а потому это, так называемые, неполярные углеводороды. С точки зрения химии, если в системе силами взаимодействия между молекулами можно пренебречь, то такую систему можно рассматривать как идеальную. К газообразным углеводородам с точки зрения физики можно применять законы для идеальных систем. С точки зрения термодинамики идеальным называется газ, внутренняя энергия которого зависит только от температуры и для которого справедливы равенства: (∂Е/∂V)T = 0, z = Р·V/Q·R·T = 1, где Е – внутренняя энергия парообразования, Дж/моль; z – коэффициент, характеризующий степень отклонения реального газа от закона идеального газа. С точки зрения математики к расчёту физико-химических свойств газа, как многокомпонентной смеси можно применять принцип аддитивности. Аддитивный подход к расчёту физико-химических и технологических параметров означает, что каждый компонент газа в смеси ведёт себя так, как если бы он в данной смеси был один. Следовательно, для оценки макроскопических свойств нефтяного газа (при н.у. и с.у.) применимы аддитивные методы расчётов физико-химических и технологических параметров (Псмеси): 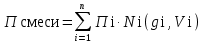 , ,где Ni – мольная доля; gi – весовая доля; Vi – объёмная доля; Пi – физико-химическое свойство i-го компонента. Для идеальных газов общее давление в системе (смеси газов) равно сумме парциальных давлений компонентов (закон Дальтона): 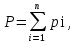 где Р – общее давление смеси газов; рi – парциальное давление i-го компонента в смеси. Откуда pi=Ni·P, 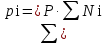 , где , где 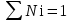 То есть, парциальное давление компонента в газовой смеси равно произведению его молярной доли на общее давление смеси газов. Аддитивность парциальных объёмов (Vi) компонентов газовой смеси выражается законом Амага: 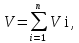 где V – общий объём смеси газов; Vi – мольный объём i-го компонента газа в смеси. По аналогии мольный объём компонента в газе можно оценить: Vi=Ni·V, Как аддитивные величины рассчитывают все физико-химические свойства газа, например, плотность смеси газов: 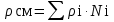 где ρi – плотность i–го компонента; Ni – мольная доля i–го компонента. Молекулярная масса смеси газовых компонентов рассчитывается по принципу аддитивности для смесей, состав которых выражен в мольных или объёмных долях: 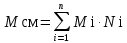 3.3. Уравнение состояния Для определения многих физических свойств природных газов используется уравнение состояния. Уравнением состояния называется аналитическая зависимость между параметрами, описывающими изменение состояние вещества. В качестве таких параметров используются давление, температура, объём. Состояние газа при нормальных и стандартных условиях описывается уравнением Менделеева–Клапейрона: 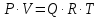 , ,где Р - абсолютное давление, Па; V - объём, м3; Q - количество вещества, моль; Т - абсолютная температура, К; R - универсальная газовая постоянная, Па·м3/(моль·град). На основе уравнения состояния газа можно рассчитывать многие параметры нефтяного газа: плотность, мольный объём, количество молекул, число молекул, парциальные давления и другие, если рассматривать количество вещества в уравнении состояния газа равное 1 молю (Q = 1 моль). С учётом этого, уравнение состояния газа можно преобразовать следующим образом: 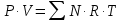 Если сумма молей равна единице (ΣN=1 моль), следует, что уравнение приобретает вид ⇒ Р·V = R·T. Зная, что масса (m) одного моля идеального газа равна его молекулярной массе (М), умножив левую и правую части на молекулярную массу и массу газа, соответственно, получим: 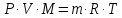 Поделив обе части на V·R·T и преобразовав, получим выражение для расчёта плотности: 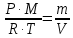 , , 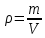 , , 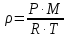 Плотность газа с возрастанием давления будет расти, а с возрастанием температуры уменьшаться. Плотность смеси газовых компонентов рассчитывают с учётом средней молекулярной массы смеси газа (Mсм) как отношение молекулярной массы смеси газа к его мольному объёму (Vм). Например, для нормальных условий плотность газа будет рассчитываться по выражению: ρсм = Mсм /22,414. Если плотность газа (ρо) задана при атмосферном давлении, равном 0,1013 МПа, то пересчёт её величины с учётом другого давления (Р) при той же температуре для идеального газа выполняется по формуле: ρ = ρо·Р/Ратм. Относительная плотность газов величина, рассчитанная по отношению к плотности воздуха, определенного при тех же условиях: ρо см = ρсм /ρвозд. Плотность воздуха (ρвозд) при н.у. равна ≈ 1,293 кг/м3, а при с.у. ≈ 1,189 кг/м3. Аналогично находится и выражение для мольного объёма: 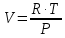 Мольный объём при давлениях, равных или близких атмосферному и, для физических процессов, когда не происходит изменения числа молей в системе, оценивается соотношением: 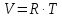 где R - универсальна газовая постоянная; Т - температура, К. С увеличением температуры мольный объём газа увеличивается. Мольный объём газов с возрастанием температуры будет расти, а с возрастанием давления уменьшаться. Уравнение состояния имеет свои граничные условия. Оно справедливо для описания поведения газов при давлениях, близких к атмосферному (от 0,1 до 1,0–1,2 МПа), и при температурах ≈ 0-20 оС. При повышенном давлении газ сжимается и его состояние отличается от поведения идеальных газов. 3.4. Состояние реальных газов При повышенных давлениях поведение нефтяного газа отклоняется от законов идеальных систем. Поведение реальных газов характеризуется межмолекулярным взаимодействием, молекулы газов начинают притягиваться друг к другу за счёт физического взаимодействия. В инженерной практике для реальных газов используется уравнение Менделеева–Клапейрона, содержащее коэффициент сверхсжимаемости z, предложенный Д. Брауном и Д. Катцом и, учитывающий отклонения поведения реального газа от идеального состояния: 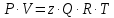 , ,где Q - количество вещества, моль; z - коэффициент сверхсжимаемости газа. Физический смысл коэффициента сверхсжимаемости заключается в расширении граничных условий для высоких давлений уравнения Менделеева-Клапейрона. Коэффициент z зависит от давления и температуры, приведенных критических давлений и температур, природы газа: 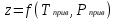 , ,где Тприв - приведенная температура; Рприв - приведенное давление. Приведёнными параметрами индивидуальных компонентов называются безразмерные величины, показывающие, во сколько раз действительные параметры состояния газа: температура, давление, объём, плотность и другие больше или меньше критических. 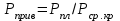 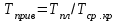 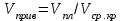 А для смесей газов они характеризуют отношения действующих (реальных) параметров (температура, давление и др.) к среднекритическим параметрам смеси: 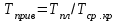 , где , где 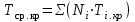 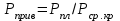 , где , где 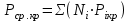 Критическая температура (Ткр) - максимальная температура, при которой газ и жидкость могут ещё сосуществовать в равновесии (табл. 3.4). Критическое давление - давление паров вещества при критической температуре (табл. 2.5), а объём вещества, отнесённый к 1 молю или к единице массы вещества, называется критическим удельным объёмом. Таблица 3.4 Критические давления и температуры компонентов нефтяных газов
Существуют графики для различных диапазонов изменения приведённых параметров, один из которых представлен ниже (рис. 3.1), эмпирические формулы и зависимости для оценки коэффициентов сверхсжимаемости от приведённых давлений и приведённых температур. При содержании неуглеводородных компонентов в составе нефтяных газов (N2, СО2, Н2S) следует вводить поправки в рассчитанные значения коэффициентов сверхсжимаемости на содержание этих соединений, используя специальные графики (рис. 3.2). Зная коэффициент сверхсжимаемости (z) и объём, занимаемый газом при нормальных условиях, можно оценить его объём при пластовых условиях по закону Бойля-Мариотта: 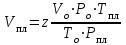 Отношение объёма газа при пластовых условиях (Vпл) к объёму газа при нормальных условиях (Vo) называется объёмным коэффициентом (b) газа: 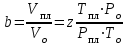 Объёмный коэффициент газа используется при пересчёте объёма, занимаемого газом при нормальных условиях на пластовые условия, и наоборот, например, при подсчёте запасов. 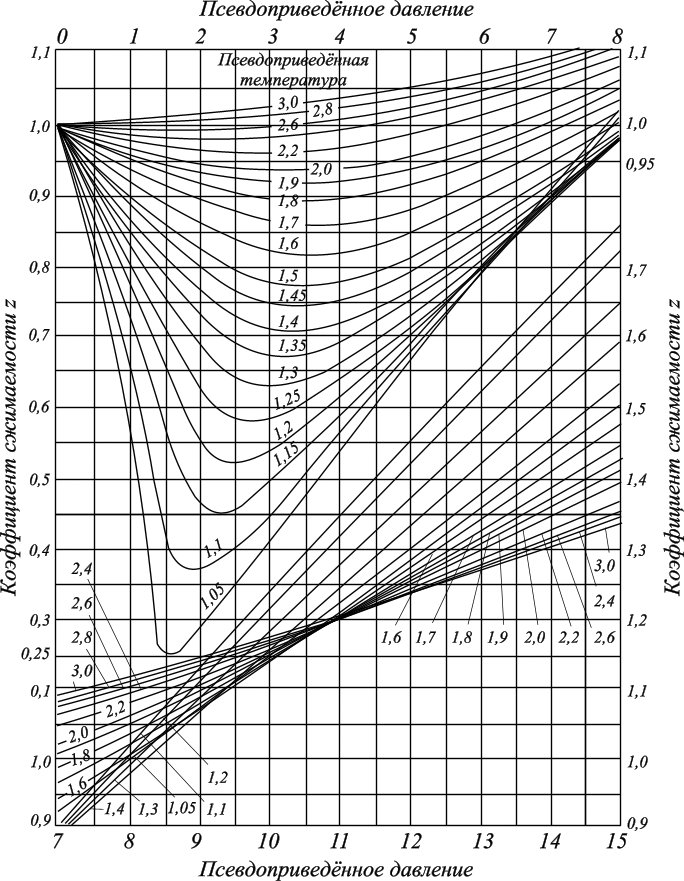 Рис. 3.1. Коэффициенты сверхсжимаемости углеводородных газов, в зависимости от приведённых параметров 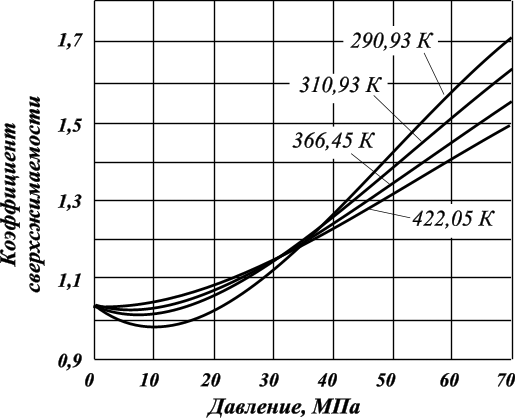 Рис. 3.2. Зависимости коэффициентов сверхсжимаемости азота от давления и температуры 3.5. Вязкость газов Вязкость газа характеризует его состояние исходя из некоторых положений кинетической теории газов. При низких давлениях и температурах динамическая вязкость газа оценивается из теории соударения частиц и зависит от средней длины пробега молекул ( λ ), от средней скорости движения молекул ( v ) и от их плотности газа: 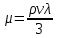 где ρ - плотность газа; λ - средняя длина пробега молекул газа; v - средняя скорость молекул газа. С возрастанием температуры средняя длина свободного пробега молекул и средняя скорость движения молекул увеличиваются, а следовательно, и вязкость газа возрастает, несмотря на уменьшение величины плотности (рис. 3.3). 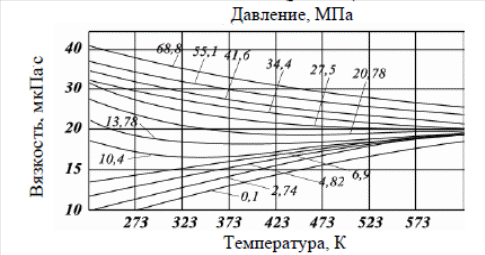 Рис. 3.3. Зависимости коэффициентов динамической вязкости нефтяного газа плотности 0,6 от температуры при различных давлениях Отмеченный характер изменения вязкости газов объясняется спецификой проявления внутреннего трения. Вязкость газа характеризует способность газа оказывать сопротивление перемещению одной части газа относительно другой. Количество движения из слоя в слой передаётся вследствие перелёта молекул газа в движущиеся относительно друг друга слои. При этом возникают силы, тормозящие движения одного слоя и увеличивающие скорость движения другого. С повышением температуры увеличивается скорость и количество движения, передаваемое в единицу времени и, как следствие, возрастает величина вязкости газа. Повышение давления от 0,1 до 1,2 МПа (рис. 3.4) не влияет на величину вязкости газа, поскольку уменьшение средней длины пробега молекулы и средней скорости движения молекулы компенсируется увеличением величины плотности. Эти закономерности при давлениях выше 1,2 МПа изменяются. Вязкость углеводородного газа при нормальных условиях невелика и не превышает значения 0,01 сантипуаза (сПз) ≈ 10 мкПа·с: 1 пуаз = 0,1 н·с/м2 = 0,1 Па·с; 1 сПз = 1 мПа·с = 1·103 мкПа·с. Неуглеводородные компоненты: азот, углекислый газ, сероводород, гелий, в том числе и воздух являются более вязкими составляющими природного газа. Величины вязкости для них изменяются в диапазоне от 0,01 до 0,025 сПз. 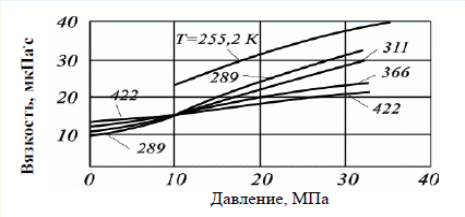 Рис. 3.4. Зависимости вязкости газа от давления при различных температурах Особое влияние на величину вязкости газа оказывает азот. При содержании в углеводородном газе более 5 % азота следует учитывать его влияние на вязкость газа и оценивать средневзвешенную вязкость смеси по принципу аддитивности: μсм = Na·μa + (1– Na)·μуг, где μсм – динамическая вязкость смеси газов; μа и μуг – динамические вязкости азота и углеводородов; Na – молярная доля азота в составе газа. |
