Физика нефтяного пласта
 Скачать 0.65 Mb.
|
Деформация нефтегазового пласта; физическая сущность; коэффициенты и способы их определения.Деформации бывают: линейные и объемные, упругие и пластичные. Упругие характеристики – упругость, пластичность, прочность на сжатие и разрыв и др. Большая часть г/п выдерживает высокие нагрузки при всестороннем сжатии. Значительно меньшие разрушение напряжения при изгибе и растяжении. Если нагружение и разгрузка г/п происходит в короткий промежуток времени, при значит диапазоне напряжений справедлив закон Гука. Если сжимающая нагрузка, составляющая иногда 10-15% от разрущающей (т. е. не превышающей предел упругости), действует длительно, в породах могут возникать явление ползучести с образованием остаточных деформаций. В отличии от явления ползучести пластичная деформации происходят при быстром нагружении пород за пределами их упругости. Явления ползучести и пластической деформации способствует частичной разгрузке продуктивных пластов призабойной зоны от воздействия горного Р – вследствие — «течения» части пород в скважину при ее строительстве под влиянием высоких нагрузок в вертикальном направлении. Поэтому давление ГРП часто оказывается значит ниже горного (до 20-40%). Со снижением пластового Р, эффективное напряжение возрастает и поэтому уменьшается объем пор вследствие упругого расширения зерен, их переукладки и более плотной упаковки. Вначале происходят упругие деформации, а при значительном снижении пластового Р, возможны остаточные деформации пород, которые не восстанавливаются в полной мере даже в процессе заводнения залежи и при увеличении Р , пластового до первоначального. Так как большинство м/р разрабатывается заводнением, то значительного снижения Р пластового не происходит. Поэтому в большинстве случаев возникают процессы упругих деформаций пористых сред. Расширяющиеся при этом г/п и пластовые жидкости находящиеся в зоне пластового Р, обладают упругим запасом, равным сумме объемов расширения пород и пластовых жидкостей. Количественно упругие изменения объема пор оценивают коэффициентом объемной упругости пласта. βс=(1/V)*(dVпор/dP), где V - объем образца породы; dVпор - изменения V пор при уменьшении или увеличении Р пластового на dP. Значение βс зависит от состава, строения и свойств г/п, а также от Р (сжимаемость сокращается с ростом P). При изменении Р, изменяется и объем жидкости, коэффициент сжимаемости которой (βж характеризуется соотношением βж=(1/V)*(dV/dP), где V - V жидкости; dV - изменение объема ж-ти при изменении Р на dP. Коэффициент сжимаемости нефтей βн, зависит от количества растворенного газа и изменяется в пределах (4 - 140)*10-10 Па-1. Для учета суммарной сжимаемости пор и жидкостей введен комплексный параметр- коэффициент упругоемкости β; β=βс+mβж. Породы, залегающие в недрах земли, находятся под влиянием горного давления. Горное давление – механические силы, которые действуют в пласте как в его природном состоянии, так и в техногенном изменении пласта. В результате действия на породу комплекса сил (веса вышележащих пород, тектонических сил, напора подземных вод, тепловых и электрических полей) порода может находиться в общем случае в условиях сложного напряжённого состояния, характеризующегося тем, что результирующие векторы напряжений не перпендикулярны поверхностям воздействия. Все вышеназванные силы обуславливают горное давление, т.е. Рг=fi, где fi – силы, действующие на пласт. Рассмотрим реальный пласт:  Н Р=gН, dР=g dr П  од действие сил на поверхность в пласте возникнут напряжения: =dF/dS.Напряжение – реакция пласта на приложенную нагрузку. В  ыберем из массива породы эллипсоидный элемент и рассмотрим реакции:Если напряжения действуют в одном направлении, то мы получим одноосное напряжённое состояние. Если напряжения действуют в плоскости в разных направлениях, мы получим плоское напряжённое состояние. Если у нас происходит изменение напряжения в объёме, возникает объёмное напряжённое состояние. При реализации эксперимента модель даёт нам одноосное напряжение, тогда как в пласте объёмное напряжённое состояние. В зависимости от того, как действует напряжение, оно подразделяется на:  z       z   zу zх    хz  уz х х   ух хуу    z   х ху хzSij ух у уz = Рik, zх zу z где - главное (нормальное) напряжение, Рik – совокупность девяти напряжений при i=k и касательных при ik. Напряжённое состояние приводит к тому, что пласт подвергается деформации. Деформация – изменение формы (объёмов, размеров) под воздействием напряжений. Напряжения можно подразделить на:  первичные – напряжения, связанные с образованием пласта; вторичные – напряжения, связанные с деятельностью человека.Напряжённое состояние может меняться с изменением температуры, электрического, магнитного поля пласта и других факторов. Деформация зависит от вида напряжённого состояния, т.о. можно выделить:  линейные деформации; сдвиговые деформации; объёмные деформации.В случае линейной деформации можно записать относительно продольную деформацию: =1/1. Нормальные составляющие напряжения обычно вызывают деформации сжатия или растяжения х, у, z. Касательные напряжения вызывают деформации сдвига ху, уz, хz (деформация сдвига обычно измеряется углами сдвига, т.к. из-за малости их величины tg=). Суммарная деформация ху, уz, хz – величина, на которую уменьшается прямой угол между соответствующими гранями выбранного нами из массива пласта куба в результате сдвига. Деформации удлинения и сдвига можно разложить на составляющие по осям координат и на их основе написать тензор деформаций:   х 1/2ху 1/2хz[Тд]= 1/2ух у 1/2уz 1/2zх 1/2zу z Т 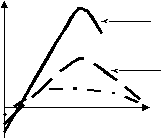 ипичные графики зависимости () выглядят следующим образом:Упруго-хрупкий тип деформации Упруго-пластичный тип деформации  Пластичный тип деформацииДля пород, слагающих пласты, нарушается закон Гука: V/V=(3(1 - 2)/Е)р, р=(х+у+z)/3 Р  ассмотрим фиктивную модель пористой среды:V0=3D3 Под воздействием давления пористая среда начинает деформироваться. V=3(D-1)33D3 - 33D31, 1=(3F(1 - 2)/(D1/2Е))2/3, где F – сосредоточенная сила, возникающая на контактах шаров. - коэффициент Пуассона. При этом напряжение можно рассчитать по следующей формуле: Р=2F/(2D2)=F/D2, где D – диаметр шара. Теперь рассмотрим объёмную деформацию. Относительное изменение объёма упаковки из шаров можно записать следующим образом: V/V=-3[3(1 - 2тв)/Етв]2/3Р2/3. Модуль объёмного (всестороннего) сжатия, или коэффициент сжимаемости породы, выражает связь между давлением и относительным изменение объёма материала: (р)=1/V(dV/dр)=2[3(1 - тв2)/Е)2/3Р-1/3 Можно видеть, что зависимость деформаций от напряжений нелинейная. Для описания изменения горных пород используются понятия деформационных сред. Деформация в многофазной среде связана с деформацией всего пласта и пор. Vпл=Vск=Vп+Vтв При изменении и пластового давления происходит изменение Vп и Vтв: -dV/V=скd+твdр, где - напряжение. -dVп/Vп=пd+твdр -dVтв/Vтв=(1/(1-kп))твd+твdр |