курсовая. Союнов_Производная26.04.22. Физикоматематический факультет Кафедра математики и методики преподавания математики
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
2.5. Применение производной при решении задач в разных науках2.5.1 Задачи по геометрииПо аналитической геометрииПример 7. Найти угол между касательной к графику функции  в точке в точке  и осью и осью 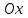 . .Решение. Найдем угловой коэффициент касательной к кривой  в точке в точке  , т.е. значение производной этой функции при , т.е. значение производной этой функции при  . .Производная функции  равна равна 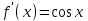 . По формуле . По формуле  находим находим  . .Пример 8. Найти уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой  . .Решение. Значение функции  и ее производной в точке и ее производной в точке  равны: равны:  . Используя формулу . Используя формулу  , найдем искомое уравнение касательной: , найдем искомое уравнение касательной: или или 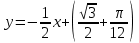 . .Пример 9. Доказать, что касательная к параболе  в точке с абсциссой в точке с абсциссой 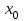 пересекает ось пересекает ось 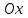 в точке в точке  . .Решение. Пусть  , тогда , тогда  и и  .По формулу .По формулу  находим уравнение касательной: находим уравнение касательной: . .Найдем точку пересечения этой касательной с осью абсцисс. Из равенства  находим находим  . .Пример 10. Найти тангенсы углов наклона касательной к кривой  в точках в точках  Решение. Имеем  ; следовательно, ; следовательно, По дифференциальной геометрии Пример 11. Найти геодезическую кривизну винтовой линии 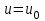 , лежащей на прямом геликоиде , лежащей на прямом геликоиде , ,  , ,  . .Решение. Запишем формулу для вычисления  : :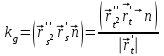 . . , , 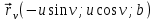 , , . .Положим  , тогда , тогда  , ,  . Применяя формулу для вычисления . Применяя формулу для вычисления  , получим , получим  . .Пример 12. Для кривой 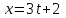 , ,  , , 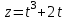 составить уравнение касательной, главной нормали, бинормали в точке составить уравнение касательной, главной нормали, бинормали в точке  . .Решение. Проверим, лежит ли точка  на кривой: на кривой: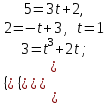 . .Точка  лежит на кривой и соответствует значению параметра лежит на кривой и соответствует значению параметра 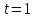 . .Напишем уравнение кривой в векторном виде:  . Тогда . Тогда 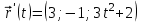 , , 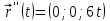 . .В точке  : :  , ,  . .Уравнение касательной в точке  имеет вид: имеет вид: . .Найдем уравнение бинормали, ее направляющий вектор коллинеарен вектору  . . , , уравнение бинормали. Найдем направляющий вектор главной нормали: уравнение бинормали. Найдем направляющий вектор главной нормали: . .Главная нормаль задается уравнением  . .Пример 13. Найти длину дуги одного витка кривой:  , , 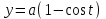 , ,  (где (где   ) между двумя ее соседними точками пересечения с плоскостью ) между двумя ее соседними точками пересечения с плоскостью 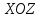 . .Решение. Данная кривая пересекает плоскость 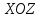 , если , если  . Отсюда следует, что . Отсюда следует, что  ; ;  и и  - значения параметра - значения параметра  между двумя соседними точками пересечения с плоскостью между двумя соседними точками пересечения с плоскостью 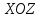 . .Тогда 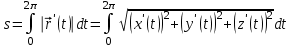 , ,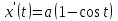 , ,  , ,  , , . .В промежутке  , поэтому , поэтому  . Следовательно , длина дуги . Следовательно , длина дуги 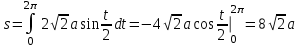 . [1, 343 ] . [1, 343 ] |
