курсовая. Союнов_Производная26.04.22. Физикоматематический факультет Кафедра математики и методики преподавания математики
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
2.5.2 Задачи по физикеПусть точка движется вдоль некоторой прямой. Выберем на прямой начало отсчета, положительное направление и единицу измерения. Тогда положение точки на прямой будет определяться ее координатой. Зависимость  называется законом движения точки. Средней скоростью движения называют отношение перемещения к промежутку времени, в течение которого это перемещение произошло. Если, скажем, точка за промежуток времени от t1 доt2 прошла путь от А до В и вернулась обратно в А, то перемещение равно 0 и средняя скорость vср равна 0. В общем случае имеем называется законом движения точки. Средней скоростью движения называют отношение перемещения к промежутку времени, в течение которого это перемещение произошло. Если, скажем, точка за промежуток времени от t1 доt2 прошла путь от А до В и вернулась обратно в А, то перемещение равно 0 и средняя скорость vср равна 0. В общем случае имеемvср =  , ,или vср =  . .Если положить   , то средняя скорость за промежуток времени , то средняя скорость за промежуток времени 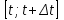 окажется равной: окажется равной:vср =  . .Мгновенной скоростью в момент времени t называют предел средней скоростью движения за промежуток 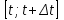 , когда , когда  . Значит, . Значит,vмгн =  . .Так как  , то мгновенная скорость прямолинейно движущейся точки есть производная координаты (пути) x по времени t. в этом состоит механический смысл производной. , то мгновенная скорость прямолинейно движущейся точки есть производная координаты (пути) x по времени t. в этом состоит механический смысл производной.Дифференциал координаты равен 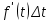 , т.е. vмгн , т.е. vмгн  . Это путь, который прошло бы тело за промежуток времени . Это путь, который прошло бы тело за промежуток времени 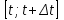 , если бы его скорость была постоянной и равнялась мгновенной скорости в момент времени t. , если бы его скорость была постоянной и равнялась мгновенной скорости в момент времени t.Пример 14. Найти мгновенную скорость при свободном падении. Решение. Закон свободного падения имеет вид  . Согласно сказанному выше vмгн = . Согласно сказанному выше vмгн =  . Значит нужно найти производную функции . Значит нужно найти производную функции  . .Дадим аргументу приращение  . Тогда . Тогда  . .Главная линейная часть приращения 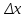 имеет вид имеет вид 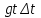 , а потому , а потому 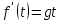 . Итак, vмгн = . Итак, vмгн = 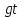 . Пример 16. Пусть . Пример 16. Пусть  - количество электричества, протекающее через поперечное сечение проводника за время - количество электричества, протекающее через поперечное сечение проводника за время  . Найдем силу тока в данный момент времени . Найдем силу тока в данный момент времени  . Решение. Если . Решение. Если 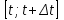 - промежуток времени, а - промежуток времени, а  - количество электричества, протекающее через поперечное сечение проводника за время - количество электричества, протекающее через поперечное сечение проводника за время  , то , то  - средняя сила тока за промежуток времени - средняя сила тока за промежуток времени  : :Iср=  . .За силу тока I в момент времени  принимается принимается  Iср. Таким образом, Iср. Таким образом, , ,т.е. сила тока есть производная от количества электричества, как функции от времени. Пример 15. Пусть дан неоднородный стержень длины  , ,  - масса части стержня длины - масса части стержня длины 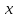 (один из концов стержня принимается за начало отсчета). Найдем линейную плотность стержня в данной точке (один из концов стержня принимается за начало отсчета). Найдем линейную плотность стержня в данной точке 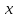 . .Решение. Если  - масса части стержня между точками, расположенными соответственно на расстоянии - масса части стержня между точками, расположенными соответственно на расстоянии 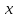 и и 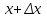 от начала отсчета, то от начала отсчета, то  - средняя линейная плотность стержня на рассматриваемом участке, а - средняя линейная плотность стержня на рассматриваемом участке, а 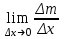 -искомая линейная плотность -искомая линейная плотность 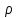 . Таким образом, . Таким образом,  , ,т.е. линейная плотность стержня в данной точке есть производная массы стержня как функции от его длины. Рассмотренные примеры показывают, как используются производная для изучения скорости протекания неравномерных процессов. При этом само понятие скорости понимается в широком смысле. Например, плотность стержня есть скорость изменения массы части стержня как функции его длины. В общем случае можно сказать так:  - средняя скорость изменения функции - средняя скорость изменения функции  на отрезке на отрезке  , а , а  - скорость изменения - скорость изменения  в данной точке. в данной точке.2.5.3. Решение экономических задач Пример 16. Выбрать оптимальный объем производства фирмой, функция прибыли которой может быть смоделирована зависимостью: π(q) = R(q) - C(q) = q2 - 8q + 10 Решение: π'(q) = R'(q) - C'(q) = 2q - 8 = 0 → qextr = 4 При q < qextr = 4 → π'(q) < 0 и прибыль убывает При q > qextr = 4 → π'(q) > 0 и прибыль возрастает При q = 4 прибыль принимает минимальное значение. Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) = p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и / или оборудования. Если же фирма способна производить больше 8 единиц, то оптимальным для фирмы будет выпуск на пределе своих производственных мощностей. Пример 17. Кривая спроса задана выражением  , где , где  - объем продаж; - объем продаж;  - цена товара в условных единицах. Объем продаж составляет 10 000. Определите, каким должно быть изменение цены товара, чтобы объем продаж возрос на 1%. - цена товара в условных единицах. Объем продаж составляет 10 000. Определите, каким должно быть изменение цены товара, чтобы объем продаж возрос на 1%.Решение. Определим цену  , соответствующую объему продаж , соответствующую объему продаж   Для оценки изменения цены товара воспользуемся формулой приближенных вычислений  По условию задачи По условию задачи  составляет 1% от 10000 или 10000/100=100. Найдем значение составляет 1% от 10000 или 10000/100=100. Найдем значение   Тогда  Таким образом, для увеличения объема продаж на 1% цена товара должна быть снижена приблизительно на 0,105 у.е. Таким образом, для увеличения объема продаж на 1% цена товара должна быть снижена приблизительно на 0,105 у.е.2.6. Вычисление пределов функции с помощью правила Лопиталя Раскрытие неопределенностей типа 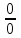 и и  . Пусть однозначные функции . Пусть однозначные функции  и и  дифференцируемы при дифференцируемы при  причем производная причем производная 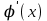 не обращается в нуль. не обращается в нуль.Если  и и  - обе бесконечно малые или бесконечно большие при - обе бесконечно малые или бесконечно большие при  т.е. если частное т.е. если частное  представляет в точке х= представляет в точке х= неопределенность типа неопределенность типа 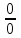 или или  , то , то 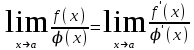 при условии, что предел отношения производных существует (правило Лопиталя). Правило применимо и в случае, когда при условии, что предел отношения производных существует (правило Лопиталя). Правило применимо и в случае, когда  . .Если частное  вновь дает неопределенность в точке х= вновь дает неопределенность в точке х= одного из двух упомянутых типов и одного из двух упомянутых типов и 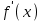 и и 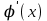 удовлетворяют всем требованиям, ранее сформулированным для удовлетворяют всем требованиям, ранее сформулированным для  и и  , то можно перейти к отношению вторых производных и т.д. , то можно перейти к отношению вторых производных и т.д.Пример 18.  Пример 19. Вычислить  (неопределенность типа (неопределенность типа  Приведя дроби к общему знаменателю, получим:  (неопределенность типа (неопределенность типа  Прежде чем применить правило Лопиталя, заменим знаменатель последней дроби эквивалентной ему бесконечно малой  Получим:  (неопределенность типа (неопределенность типа  По правилу Лопиталя  Далее, элементарным путем находим:  2.7. Отбор кратных корней уравнения Применение производной позволяет не только убедиться в существовании кратных корней (если они есть), но и дать способ отобрать все кратные корни, отделив их от простых корней. Имеет место следующее утверждение: Наибольший общий делитель многочленов  и и 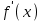 имеет своими корнями лишь корни многочлена имеет своими корнями лишь корни многочлена  , причем только те из них, которые имеют кратность не меньше 2. Каждый их этих кратных корней многочлена , причем только те из них, которые имеют кратность не меньше 2. Каждый их этих кратных корней многочлена  является корнем наибольшего общего делителя кратности на единицу ниже. Простые корни многочлена является корнем наибольшего общего делителя кратности на единицу ниже. Простые корни многочлена  не являются корнями наибольшего общего делителя многочленов не являются корнями наибольшего общего делителя многочленов  и и 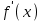 . .Отсюда вытекает следующее правило для нахождения кратных корней уравнения: 1. Находим 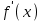 . .2. Находим наибольший общий делитель многочленов  и и 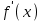 . .3. Находим корни наибольшего общего делителя многочленов  и и 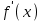 . .Каждый из найденных корней наибольшего общего делителя многочленов  и и 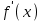 является корнем многочлена является корнем многочлена  , причем кратность этого корня на единицу больше его кратности в наибольшем общем делителе. , причем кратность этого корня на единицу больше его кратности в наибольшем общем делителе.Отметим, что если наибольший общий делитель многочленов  и и 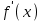 есть константа, то уравнение есть константа, то уравнение  =0 не имеет кратных корней. =0 не имеет кратных корней.Пример 20. Решить уравнение  . .Решение. Рассмотрим многочлен  производная которого равна  Найдем наибольший общий делитель многочленов  и и 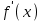 . .Имеем  - наибольший общий делитель многочленов Таким образом, наибольший общий делитель многочленов  и и 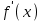 равен х-1 (с точностью до постоянного множителя). равен х-1 (с точностью до постоянного множителя).Так как х=1 является простым корнем наибольшего общего делителя, что число х=1 будет двукратным корнем данного уравнения, и, значит, многочлен  делится без остатка на делится без остатка на  Разделив Разделив  на на 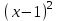 , находим, что , находим, что  Следовательно, корни исходного уравнения- это числа Следовательно, корни исходного уравнения- это числа  и х=6 и только они. и х=6 и только они.ЗАКЛЮЧЕНИЕ Изучив материал в количестве 4 источников были решены и поставлены задачи исследования и достигнута цель работы. В представленной работе материал структурирован. Общий объем работы 25 страниц. Работа содержит две главы, в первой главе «Понятия необходимые для решения математических задач с помощью производной» даны понятия производной, предела функции, интеграла, дифференциала функции. Во второй главе «Применение производной к решению задач» описано исследование функции, применение производной при решении задач в разных науках, таких как геометрия, физика, вычисление интегралов, доказательство неравенств, вычисление пределов (правило Лапиталя). Было решено 20 примера, из них самостоятельно составлено 5 примеров. Работа по данной теме способствовала формированию поисковых и исследовательских навыков, развитию логического и конструктивного мышления. Работа по данной теме интересна, и поэтому будет продолжено ее исследование в методическом аспекте. СПИСОК ЛИТЕРАТУРЫ Задачнике по курсу математического анализа. Часть1: Учеб. пособие / Н. Я. Виленкин [и др.]; под. ред. Н. Я. Виленкин. –Москва: Просвещение, 1997. -343с. Пискунов Н.С. Дифференциальное и интегральное исчисление / Н.С. Пискунов, С. Н. Пискунов. - Москва: Интеграл-Пресс, 2002.-416 с. Сборник задач по математическому анализу. Том1. Предел. Непрерывность. Дифференцируемость: Учеб. пособие / Л. Д. Кудрявцев [и др.]; под. ред. Л.Д. Кулявцева. -2-е изд. –Москва: перераб. -ФИЗМАТЛИТ, 2003. -496с Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления /Г. М. Флоринского, М. Г. Флоринского. Москва: -ФИЗМАТЛИТ, 2003. -680с. |
