голографическое хранение информации. Курсовая работа. Физикотехнический институт
 Скачать 212.15 Kb. Скачать 212.15 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ им В. И. ВЕРНАДСКОГО» ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ Кафедра общей физики ГОЛОГРАФИЧЕСКОЕ ХРАНЕНИЕ ИНФОРМАЦИИ Курсовая работа По дисциплине «Квантовая электроника» студента 4 курса группы Ф-б-о 182 Максимова Дмитрия Викторовича Направления подготовки 03.03.02 «Физика» (код и наименование) Научный руководитель _____________________ Воляр А. В. (подпись, дата) _____________________ (оценка) Симферополь, 2021 СОДЕРЖАНИЕ РЕФЕРАТ…………………………………………………………………………3 ВВЕДЕНИЕ…………………………………………………………..…………...4 ГЛАВА 1. СУТЬ ЯВЛЕНИЯ ГОЛОГРАФИИ……………………………….5 ГЛАВА 2. ГОЛОГРАФИЧЕСКАЯ ЗАПИСЬ ИНФОРМАЦИИ…………..8 2.1. Принцип голографической записи …………………………………..8 2.2. Голограммы Фурье…………………………………………………...10 ГЛАВА 3. МЕТОДЫ ВОСПРОИЗВЕДЕНИЯ ИНФОРМАЦИИ………….19 ГЛАВА 4. ВИДЫ ГОЛОГРАММ……………………………………………..21 4.1. Мультикомплексные голограммы…………………………………...21 4.2. Пространственное мультиплексирование…………………………..21 4.3. Цветные голограммы…………………………………………………21 4.4. Сканирующий опорный пучок……………………………………….22 ГЛАВА 5. ПРИМЕНЕНИЕ ГОЛОГРАФИИ В ТЕХНОЛОГИИ И ОПТОТЕХНИКЕ……………………………………………………………….23 ЗАКЛЮЧЕНИЕ……………………………………………………………...…24 СПИСОК ЛИТЕРАТУРЫ………………………………….…………………25 РЕФЕРАТГолографическое хранение информации. Симферополь ФТИ КФУ им. В. И. Вернадского, 2021 – 25 стр., 3 ил., 5 ист. Цель: целью данной курсовой работы является рассмотрение голографического хранения информации. В данной курсовой работе мы разобрались с принципом голографической записи, и последующим хранением информации. Были рассмотрены такие пункты, как: голограмма Фурье, методы воспроизведения информации. ГОЛОГРАММА, ХРАНЕНИЕ ИНФОРМАЦИИ, ГОЛОГРАММА ФУРЬЕ. ВВЕДЕНИЕ Оптика - раздел физики, в котором изучаются оптическое излучение (свет), его распространение и явления, наблюдаемые при взаимодействии света с веществом, - относится к числу наиболее старых и хорошо освоенных областей науки. Примерно до середины XX столетия казалось, что оптика как наука закончила развитие. Однако в последние десятилетия в этой области физики произошли революционные изменения, связанные как с открытием новых закономерностей (принципы квантового усиления, лазеры), так и с развитием идей, основанных на классических и хорошо проверенных представлениях. Здесь, прежде всего, имеется в виду голография, которая значительно расширяет область практического использования волновых явлений и дает толчок теоретическим исследованиям. Голография (от греч. holos - весь и grapho – пишу, т.е. «полная запись») – особый способ записи и последующего восстановления волнового поля, основанный на регистрации интерференционной картины. Она обязана своим возникновением законам волновой оптики – законам интерференции и дифракции. Этот принципиально новый способ фиксирования и воспроизведения пространственного изображения предметов изобретен английским физиком Д. Габортом (1900-1979) в 1947г. (Нобелевская премия 1971г.). экспериментальное воплощение и дальнейшая разработка этого способа (советским ученым Ю.Н.Денисюком в 1962г. и американскими физиками Э. Лейтом и Ю. Упатниексом в 1963г. стали возможными после появления в 1960г. источников света высокой степени когерентности – лазеров. Методы голографии (запись голограммы в трехмерных средах, цветное и панорамное голографирование и т.д.) находят все большее развитие. Она может применяться в ЭВМ с голографической памятью, голографическом электронном микроскопе, голографическом кино и телевидении, голографической интерферометрии и т.д. ГЛАВА 1. СУТЬ ЯВЛЕНИЯ ГОЛОГРАФИИ Согласно принципу Гюйгенса — Френеля, можно восстановить картину волнового поля, образованного электромагнитной волной, в любой момент времени и в любой точке пространства. Для этого надо записать распределение амплитуд и фаз волн (в данном случае световых) на произвольной поверхности или ее части, охватывающей источник волн. Иными словами, чтобы «заморозить» электромагнитные волны во всем пространстве, достаточно «заморозить» их только на некоторой поверхности. Как восстановить в пространстве световую волну, т. е. «разморозить» ее? Для этого надо задать параметры, характеризующие среду. Предположим, нужно восстановить плоскую волну. Для этого мы должны задать для любой плоскости равномерно распределенные источники колебаний с определенной начальной фазой. Элементарные источники колебаний должны находиться на поверхности, перпендикулярной направлению распространения волн. Но это те обязательно. Все будет зависеть от типа волн. Возьмем для примера сферические волны, излучаемые точечным источником. Зададим в качестве поверхности, на которой «замораживаются» волны, сферу с центром в источнике. Амплитуды и фазы элементарных источников волн будут одинаковыми для всей поверхности. В случае с круговыми волнами при «замораживании» световых волн надо расположить элементарные источники колебаний с одинаковой фазой и амплитудой на концентрических окружностях. Иными словами, мы должны зарегистрировать на некоторой поверхности мгновенные картины линий постоянной фазы в виде чередующихся прозрачных и непрозрачных областей. В этом нам помогает интерференция: мы получаем интерференционную картину, состоящую из светлых, (прозрачных) и темных (непрозрачных) полос. Интерференция и есть способ сравнения пространственной структуры двух пучков света. Вначале происходит их сравнение, а затем — регистрация их на фотопластинку. Откуда возникли оба эти пучка и что они собой представляли в опытах Габора? Один пучок отражался от освещенного предмета и падал на фотопластинку. Он являл собой определенную комбинацию волн, конфигурация которых зависела от формы предмета. Она могла быть как очень простой, так и очень сложной. Другой пучок имел простую конфигурацию. Чаще всего он состоял из плоских волн. Создавался он когерентным источником света и назывался опорной волной. Второй пучок служил в качестве эталона. Он также падал на фотопластинку. Оба световых пучка пересекались вблизи этой пластинки. При пересечении они интерферировали между собой, образуя области усиления или ослабления, чередующиеся по определенному закону во времени и пространстве. В результате интерференции получалась интерферограмма в виде чередующихся светлых и темных полос — неподвижная интерференционная картина. Неподвижность интерференционной картины в пространстве обеспечивалась опорной (эталонной) волной. Это она «останавливала» («замораживала») световую волну. Чтобы восстановить изображение предмета, достаточно осветить голограмму только опорным пучком, используемым при записи. Этот способ регистрации волнового поля ценен тем, что допускает простое восстановление исходной волны. Как только мы направляем на голограмму опорную волну, использованную при записи, за голограммой восстанавливается («размораживается») исходное волновое поле предмета. Согласно принципу Гюйгенса — Френеля, восстановлением мы обязаны эквивалентным источникам, образованным светлыми местами интерференционной картины. По этой причине волны «размораживаются», и наблюдатель видит пространственное изображение предмета. Итак, можно сделать вывод о том, что голография — это фотографический метод. Но он существенно отличается от метода классической фотографии. Это радикально иной, двухступенчатый метод. В отличие от обычной фотографии изображения, которые получаются при восстановлении записанного на голограмме, полностью неотличимы от изображений реального предмета. Голография позволяет воспроизвести в пространстве действительную картину электромагнитных волн, т.е. волновую картину предмета тогда, когда самого предмета уже нет. ГЛАВА 2. ГОЛОГРАФИЧЕСКАЯ ЗАПИСЬ ИНФОРМАЦИИ 2.1. Принцип голографической записи В отличие от фотографирования, регистрирующего лишь интенсивность волны, идущей от объекта, метод голографии позволяет записывать как амплитуду, так и фазу световых колебаний в плоскости наблюдения. В основе голографической записи лежит идея, согласно которой для выявления фазовой информации надо создать интерференцию исследуемой (объектной) волны с некоторой вспомогательной (опорной) волной. Будем описывать световые колебания объектной O и опорной R волн в точке M, лежащей в плоскости наблюдения, соответственно в виде выражений 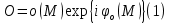 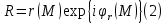 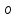 , , 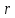 , , 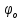 , , 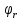 - соответственно амплитуды и фазы колебаний. Если в плоскости наблюдения расположить фотопластинку с идеальной линейной по интенсивности фотоэмульсией, то она зарегистрирует следующее распределение интенсивности: - соответственно амплитуды и фазы колебаний. Если в плоскости наблюдения расположить фотопластинку с идеальной линейной по интенсивности фотоэмульсией, то она зарегистрирует следующее распределение интенсивности: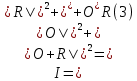 После соответствующей обработки пропускание пластинки станет пропорционально I. Если теперь эту пластинку осветить опорной волной R, то поле на выходе пластинки будет иметь вид 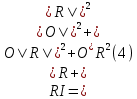 Последнее выражение составляет теоретическую основу голографии. В нем первое слагаемое 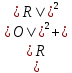 представляет собой поле опорной волны R, амплитуда которой промодулирована коэффициентом представляет собой поле опорной волны R, амплитуда которой промодулирована коэффициентом 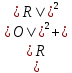 ; второе слагаемое ; второе слагаемое 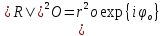 - поле объектной волны, амплитуда которой промодулирована коэффициентом - поле объектной волны, амплитуда которой промодулирована коэффициентом 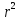 . Если в качестве опорной волны используется плоская волна, то . Если в качестве опорной волны используется плоская волна, то 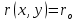 и модуляция исчезает; объектная волна при этом равномерно ослабевает в соответствии с коэффициентом и модуляция исчезает; объектная волна при этом равномерно ослабевает в соответствии с коэффициентом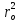 . Наконец, третье слагаемое в последнем выражении . Наконец, третье слагаемое в последнем выражении 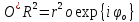 - описывает волну, комплексно-сопряженную с объектной волной. Оно несет информацию, хотя и очень близкую к информации об объекте, но отличающуюся от объектной волны наличием обратной фазы. - описывает волну, комплексно-сопряженную с объектной волной. Оно несет информацию, хотя и очень близкую к информации об объекте, но отличающуюся от объектной волны наличием обратной фазы. Остановимся теперь на конкретных схемах голографической записи и восстановления изображений. Наибольшее распространение получила схема, предложенная в 1962 г. американскими учеными Лейтом и Упатниексом. Ее упрощенный вариант приведен на рис. 2.1. 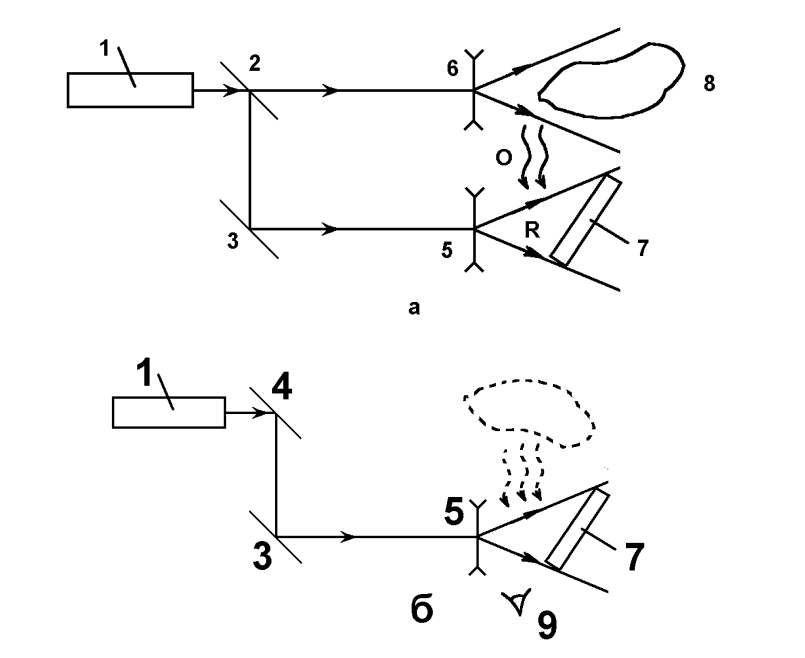 Рис. 2.1. Схема записи (а) и восстановления (б) изображения: 1 - лазер; 2 - светоделительная пластина; 3,4 - поворотные зеркала; 5,6 - линзы; 7 - голографическая пластина; 8 - объект; 9 - наблюдатель; О - объектная волна; R - опорная волна. Как видно из рисунка, при восстановлении изображения используется пучок, который при записи выполняет роль опорного. Положение восстановленного изображения полностью соответствует положению объекта. Другая схема, ориентированная на получение так называемых голограмм Фурье, будет далее рассмотрена более подробно. 2.2. Голограммы Фурье Рассмотрим приведенную на рис. 2.2 схему получения голограммы Фурье с точечным опорным источником, расположенным на оси системы. Такая схема рассчитана на получение голограмм плоских предметов, как правило - изображений различных объектов на фотопленке. Голограммы Фурье широко используются для оптической обработки информации, а также в системах голографической памяти. 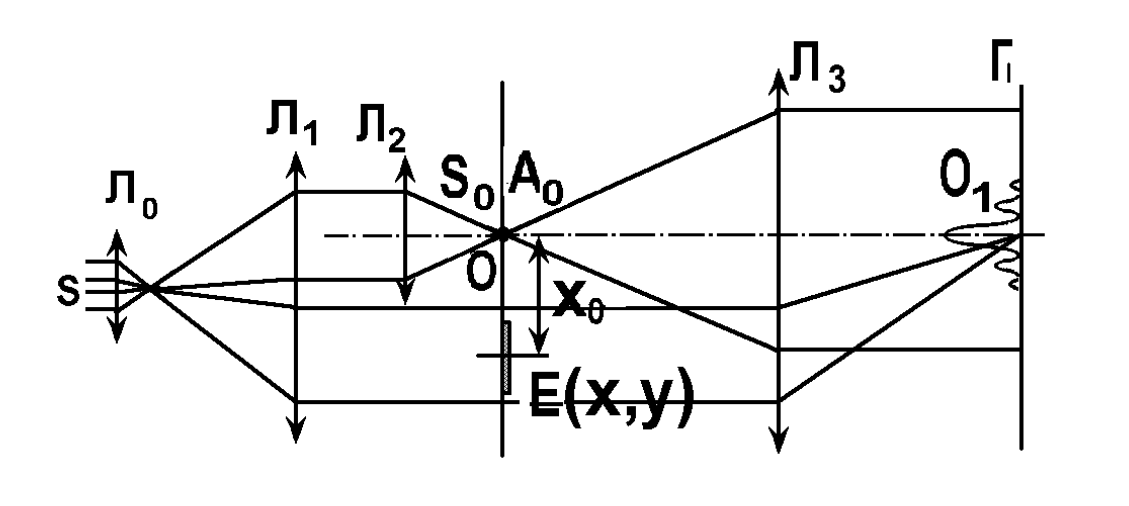 Рис. 2.2. Схема получения голограммы Фурье На схеме плоскость, в которой размещается пленка с изображениями объектов, обозначена буквой П, а плоскость, в которой формируется голограмма, - буквой Г. Плоскости П и Г совпадают с фокальными плоскостями линзы 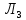 . На плоскость П падает плоская волна когерентного света, создаваемая источником S. От этого же источника в плоскости П с помощью линз . На плоскость П падает плоская волна когерентного света, создаваемая источником S. От этого же источника в плоскости П с помощью линз 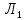 и и 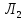 формируется точечный источник формируется точечный источник 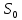 , создающий опорную волну. Опорный и предметный пучки собираются линзой , создающий опорную волну. Опорный и предметный пучки собираются линзой 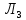 и в плоскости Г создают интерференционную картину, которая регистрируется помещенной в этой плоскости фотопленкой. и в плоскости Г создают интерференционную картину, которая регистрируется помещенной в этой плоскости фотопленкой.Выберем в плоскости П систему координат 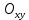 , а в плоскости Г - систему , а в плоскости Г - систему 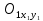 . Расположим начала координат этих систем на оптической оси линзы . Расположим начала координат этих систем на оптической оси линзы 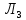 . Точечный опорный источник . Точечный опорный источник 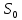 поместим в начало координат системы поместим в начало координат системы 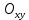 . Комплексное световое поле, образованное источником S в плоскости фотопленки, обозначим двумерной функцией h(x, y). Комплексное световое поле в плоскости Г обозначим через . Комплексное световое поле, образованное источником S в плоскости фотопленки, обозначим двумерной функцией h(x, y). Комплексное световое поле в плоскости Г обозначим через 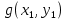 . Линза . Линза 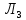 выполняет над функцией h(x, y) двумерное преобразование Фурье, так что функции h(x, y) и выполняет над функцией h(x, y) двумерное преобразование Фурье, так что функции h(x, y) и 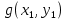 связаны следующей зависимостью: связаны следующей зависимостью: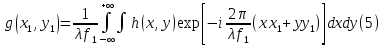 где λ - длина волны когерентного света источника S, 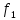 - фокусное расстояние линзы - фокусное расстояние линзы 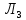 . Запишем последнее выражение в несколько иной форме: . Запишем последнее выражение в несколько иной форме: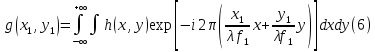 из которой видно, что в подынтегральном выражении роль пространственных частот играют величины 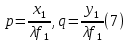 Иначе: 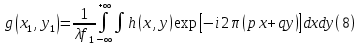 Таким образом: 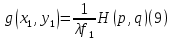 где H(p, q) - двумерное преобразование Фурье функции h(x, y), а p и q определяются равенствами (7). Будем называть H(p, q) - комплексным спектром функции h(x, y), а его составляющие A(p, q) и 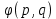 в соответствии с выражением в соответствии с выражением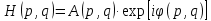 - амплитудным и фазовым спектрами. Вернемся к схеме рис. 2.2 и составим выражение для функции h(x,y). Как видно из рисунка, эта функция образуется двумя компонентами: полем опорного источника и полем, прошедшим пленку с изображением объекта. Так как мы рассматриваем опорный источник в виде идеальной точки, обозначим его поле с помощью двумерной дельта- функции Дирака с амплитудой волны  , т.е. , т.е.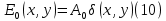 Поле центрированного объекта обозначим через 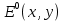 . Ввиду того, что в принятой схеме объект смещен относительно начала координат на величину . Ввиду того, что в принятой схеме объект смещен относительно начала координат на величину 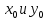 , то поле будет характеризоваться функцией , то поле будет характеризоваться функцией 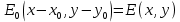 . Таким образом, получим: . Таким образом, получим: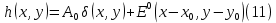 Поле в плоскости Г определим в соответствии с выражением (8). Как известно, преобразование Фурье суммы функций равно сумме преобразований Фурье слагаемых, поэтому получим комплексные спектры слагаемых раздельно. Для первого слагаемого, вспоминая, что по одному из определений дельта- функции 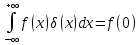 , получим: , получим: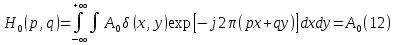 Для второго слагаемого: 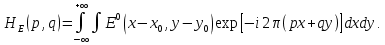 Делая подстановку: 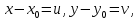 Получим 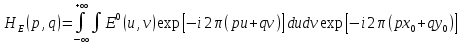 Или 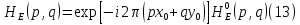 Где 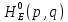 – комплексный спектр центрированного объекта. – комплексный спектр центрированного объекта.Таким образом, учитывая, что 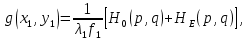 Из (12) и (13) получим: 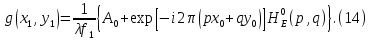 Комплексный спектр 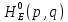 центрированного объекта через амплитудный и фазовый спектры выразится следующим образом: центрированного объекта через амплитудный и фазовый спектры выразится следующим образом: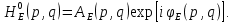 Поэтому для поля (14) будем иметь: 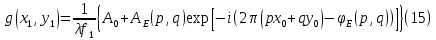 Голограмма получается регистрацией поля в плоскости Г на фотопленку. Ввиду того, что фотографическая эмульсия реагирует на интенсивность света I(p, q), прозрачность пленки τ(p, q) (амплитудное пропускание) является функцией интенсивности: 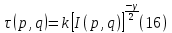 где γ - коэффициент контрастности пленки. Коэффициент k определяется чувствительностью фотослоя и временем экспозиции. Интенсивность светового поля в плоскости Г равна квадрату модуля функции  , т.е. , т.е.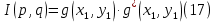 Где 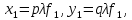 а звездочкой обозначена комплексно-сопряженная величина. Подставив в (17) вместо 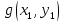 ее значение из (15), получим: ее значение из (15), получим: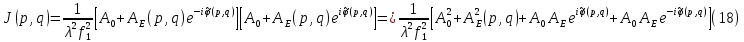 Здесь 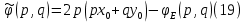 Учитывая, что 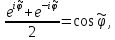 получим: получим: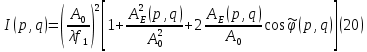 Функцию прозрачности голограммы получим, подставив (20) в (16). При  , достаточно больших по сравнению с , достаточно больших по сравнению с  , разлагая (16) в степенной ряд и ограничиваясь линейным приближением, получим: , разлагая (16) в степенной ряд и ограничиваясь линейным приближением, получим: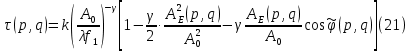 Запишем полученное выражение в более удобной для анализа форме: 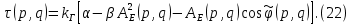 Здесь 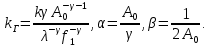 Соотношение (22) является уравнением голограммы Фурье, полученной по схеме рис. 2.2. но представляет собой связь амплитудного пропускания τ(p,q) голограммы с пространственно-частотными характеристиками голографируемого плоского предмета. С точностью до разрешающей способности фотопленки и в пределах линейности ее характеристики на голограмме зафиксирована вся информация о предмете, содержащаяся в его амплитудном 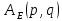 и фазовом и фазовом 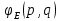 спектрах. Для сведения к минимуму нелинейных искажений при формировании голограммы необходимо правильно выбирать входящие в уравнение параметры kΓ, α и β, а следовательно, и определяющие их амплитуду спектрах. Для сведения к минимуму нелинейных искажений при формировании голограммы необходимо правильно выбирать входящие в уравнение параметры kΓ, α и β, а следовательно, и определяющие их амплитуду 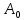 опорного пучка и коэффициент контрастности γ. Обычно принимают опорного пучка и коэффициент контрастности γ. Обычно принимают 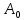 >10 >10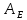 и γ ≈ 2. и γ ≈ 2. Проанализируем уравнение голограммы (22). В правой части уравнения содержится три слагаемых. Постоянная составляющая 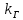 α = α = 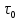 определяет среднюю прозрачность голограммы, которая получилась бы в случае перекрывания пучка от предмета, т.е. когда определяет среднюю прозрачность голограммы, которая получилась бы в случае перекрывания пучка от предмета, т.е. когда 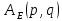 = 0. = 0.Вторая составляющая 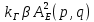 характеризует дополнительную неравномерную засветку голограммы пучком от предмета. Так как эта составляющая вычитается из характеризует дополнительную неравномерную засветку голограммы пучком от предмета. Так как эта составляющая вычитается из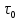 , то она уменьшает прозрачность голограммы, особенно в тех местах, где велико значение амплитудного спектра предмета. Ввиду того, что для большинства предметов наибольшую энергию несут низкочастотные составляющие спектра, потемнение голограммы Фурье за счет второй составляющей сосредоточено вблизи начала координат частотной плоскости. , то она уменьшает прозрачность голограммы, особенно в тех местах, где велико значение амплитудного спектра предмета. Ввиду того, что для большинства предметов наибольшую энергию несут низкочастотные составляющие спектра, потемнение голограммы Фурье за счет второй составляющей сосредоточено вблизи начала координат частотной плоскости.Вторая составляющая содержит лишь часть информации о предмете, так как в ней отсутствует фазовый спектр. Полную информацию содержит третья составляющая, возникающая благодаря интерференции предметного пучка с опорным. Из-за наличия в ней функции 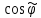 она знакопеременная. При положительном значении косинуса она уменьшает прозрачность голограммы, при отрицательном- увеличивает. Эта составляющая представляет собой косинусную волну, промодулированную по амплитуде и фазе. Вектор несущей частоты косинусоиды имеет составляющие она знакопеременная. При положительном значении косинуса она уменьшает прозрачность голограммы, при отрицательном- увеличивает. Эта составляющая представляет собой косинусную волну, промодулированную по амплитуде и фазе. Вектор несущей частоты косинусоиды имеет составляющие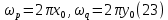 зависящие от смещения предмета относительно опорного источника. Направление фронта волны косинусоиды получим из соотношения (19) для фазы. Полагая 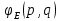 = 0, из (19) получим: = 0, из (19) получим: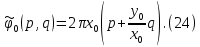 Так как фронт волны соединяет точки с одинаковой фазой, то, положив 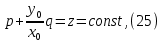 Получим уравнение фронта косинусоиды: 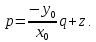 Это прямая, имеющая наклон k 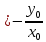 . Косинусная волна, на голограмме, проявляется в виде периодических интерференционных полос и особенно хорошо видна при равномерных . Косинусная волна, на голограмме, проявляется в виде периодических интерференционных полос и особенно хорошо видна при равномерных 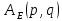 и и 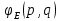 , т.е. когда она не сильно искажена модуляцией. Таким образом, объект на голограмме представляется в виде суперпозиции элементарных косинусоид. Этим и объясняется, почему этот способ записи получил название голографии Фурье. Следует отметить, что фазовый спектр , т.е. когда она не сильно искажена модуляцией. Таким образом, объект на голограмме представляется в виде суперпозиции элементарных косинусоид. Этим и объясняется, почему этот способ записи получил название голографии Фурье. Следует отметить, что фазовый спектр 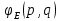 , входящий в выражение для , входящий в выражение для 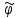 , есть фазовый спектр центрированного объекта, ибо смещение объекта на величины , есть фазовый спектр центрированного объекта, ибо смещение объекта на величины 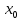 и и 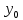 от центра учитывается первым слагаемым в (19). Поэтому для всех объектов, имеющих центральную симметрию (двумерный аналог четности функций), от центра учитывается первым слагаемым в (19). Поэтому для всех объектов, имеющих центральную симметрию (двумерный аналог четности функций), 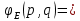 0. 0.Отметим также, что голограмма Фурье любого вещественного объекта имеет центральную симметрию. Это следует из того, что уравнение голограммы таких объектов инвариантно по отношению к перемене знака пространственных частот, ибо входящие в него члены 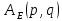 и и 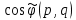 не изменяют знака при изменении знаков p и q, первый вследствие центральной симметрии, а второй - вследствие четности. При восстановлении голограммы она освещается параллельным пучком света (рис. 2.3) Каждая косинусоидальная решетка при этом сформирует изображение соответствующей точки в бесконечности. Если же сразу за голограммой установить линзу, то изображения всех точек перенесутся из бесконечности в фокальную плоскость линзы. Изображение объекта и сопряженное ему изображение будут располагаться симметрично относительно оси. На оси будет располагаться светлое пятно, обусловленное наличием первых двух слагаемых в уравнении голограммы. не изменяют знака при изменении знаков p и q, первый вследствие центральной симметрии, а второй - вследствие четности. При восстановлении голограммы она освещается параллельным пучком света (рис. 2.3) Каждая косинусоидальная решетка при этом сформирует изображение соответствующей точки в бесконечности. Если же сразу за голограммой установить линзу, то изображения всех точек перенесутся из бесконечности в фокальную плоскость линзы. Изображение объекта и сопряженное ему изображение будут располагаться симметрично относительно оси. На оси будет располагаться светлое пятно, обусловленное наличием первых двух слагаемых в уравнении голограммы. Рис.2.3. Восстановление голограммы Фурье: 1-голографическая фотопластинка; 2-линза. В заключение заметим, что воспроизведение большого диапазона значений прозрачности голограммы Фурье, полученной по схеме рис. 2.2, является сложной задачей, особенно при синтезе цифровых голограмм. Одним из путей устранения этой трудности является переход к схеме с рассеивателем. Эта схема отличается от предыдущей лишь тем, что перед предметом, установленным в плоскости П, помещается рассеиватель - тонкая прозрачная пластинка с неровной поверхностью (матовое стекло), не изменяющая амплитуду, но изменяющая случайным образом фазу в каждой точке падающей на предмет волны. Введенная таким образом случайная фаза не влияет на изображение предмета, получаемое при восстановлении, так как фотослой, регистрирующий изображение, чувствителен лишь к интенсивности восстановленной волны. В то же время она существенным образом перераспределяет энергию в частотной плоскости, т.е. в плоскости голограммы, значительно уменьшая требуемую фотографическую ширину фотослоя. ГЛАВА 3. МЕТОДЫ ВОСПРОИЗВЕДЕНИЯ ИНФОРМАЦИИ Уширенный с помощью простого оптического устройства пучок лазера одновременно направляется на исследуемый объект и на зеркало. Отраженная от зеркала опорная волна и рассеянная объектом световая волна падают на обычную фотопластинку, где происходит регистрация возникшей сложной интерференционной картины. После соответствующей экспозиции фотопластинку проявляют, в результате чего получается так называемая голограмма — зарегистрированная на фотопластинке интерференционная картина, полученная при наложении опорной и предметной волн. Голограмма внешне похожа на равномерно засвеченную пластинку, если не обращать внимания на отдельные кольца и пятна, возникшие вследствие дифракции света на пылинках и не имеющие отношения к информации об объекте. Для восстановления волнового поля предмета, тем самым для получения его объемного изображения, голограмму помещают в то место, где была расположена фотопластинка при фотографировании, и затем освещают голограмму световым пучком того же лазера под тем же углом, под которым было осуществлено экспонирование. При этом происходит дифракция опорной волны на голограмме, и мы видим объемное со всеми присущими самому объекту свойствами (в нем сохраняется также распределение освещенности, как и в объекте) «мнимое» изображение. Оно кажется нам настолько реальным, что даже иной раз появляется желание потрогать предмет. Разумеется, это невозможно, так как в данном случае изображение образовано голографической копией волны, рассеянной предметом во время записи голограммы. От голограммы в глаз попадает точно такая же волна, какая попала бы от самого предмета. Кроме мнимого изображения получается также действительное изображение объекта, имеющее рельеф, противоположный рельефу самого объекта, если наблюдение ведется справа от голограммы. В этом случае трудно наблюдать действительное изображение невооруженным глазом. Если осветить голограмму с обратной стороны обращенным опорным пучком так, чтобы все лучи пучка были направлены противоположно лучам первоначального опорного пучка, то в месте первоначального расположения предмета возникает действительное изображение, доступное наблюдению невооруженным глазом. Его можно зарегистрировать на фотопластинку без применения линз. ГЛАВА 4. ВИДЫ ГОЛОГРАММ 4.1. Мультикомплексные голограммы Мультикомплексной называют такую голограмму, на которой одновременно записано много изображений, либо раздельно записаны отдельные части одного изображения, либо единственное изображение записано несколько раз. 4.2. Пространственное мультиплексирование При решении задачи хранения данных для записи многих голограмм можно использовать единственную фотопластинку или какой-либо иной материал, причем каждая голограмма может независимо восстанавливать изображения записанных на ней данных. При этом голограммы могут образовывать решетку типа шахматного поля, а для считывания изображения с каждой голограммы лазерный луч сканирует по решетке. Встречается и другой способ пространственного разделения голограммы, когда одна и та же объектная волна или волна от одного и того же объекта, но с разных ракурсов записывается на голограмме в виде полос. В первом случае полосковая голограмма просто повторно записывается много раз, так чтобы можно было восстановить изображение со всей голограммы. Второй случай имеет место при записи синтезированных голограмм для целей отображения информации. 4.3. Цветные голограммы Цветными называют голограммы, способные воспроизводить цветные изображения. В сущности, цветные голограммы — это мультиплексные голограммы, восстанавливающие перекрывающиеся изображения, каждое в своем цвете. Как и в случае мультиплексных голограмм, возникают различные проблемы в зависимости от того используются ли тонкие, т. е. поверхностные, голограммы или регистрирующая среда имеет заметную толщину. Голограммы, записанные на тонком материале, восстанавливают многократно повторяющиеся изображения, которые соответствуют многим дифракционным порядкам. Голограммы, записанные в толстой среде из-за усадки или набухания эмульсии могут не восстанавливаться освещением с исходной длиной волны. Если, например, рассматривать красные и белые изображения, то в противоположность черным и белым необходимо учитывать эффекты дисперсии. В случае голограммы сфокусированного изображения, поскольку расстояние между голограммой и телеграфируемым изображением; оказывается более коротким, таких проблем возникает меньше. 4.4. Сканирующий опорный пучок В случае сканирования опорным пучком объект освещается целиком, но при этом опорный пучок сканирует по голограмме. Следовательно, можно увеличить полную интенсивность света, падающего на часть голограммы, и уменьшить время экспозиции для части голограммы. Это позволяет голографировать объекты, имеющие движение в ограниченных пределах. Однако такой мет приводит к уменьшению дифракционной эффективности, что объясняется увеличением энергии опорного пучка по отношению к объектному. ГЛАВА 5. ПРИМЕНЕНИЕ ГОЛОГРАФИИ В ТЕХНОЛОГИИ И ОПТОТЕХНИКЕ В ряде технологических процессов можно использовать образуемые голограммами действительные изображения. При просвечивании голограмм мощным лазером можно наносить на обрабатываемые поверхности сложные узоры. В частности, голограммы уже применялись для бесконтактного нанесения микроэлектронных схем. Основные преимущества голографических методов перед обычными – контактными или проекционными – достижение практически безаберрационного изображения на большом поле. Предел разрешения голограммы может достигать долей длины световой волны. На изображение практически не влияют пылинки, осевшие на голограмму, царапины и другие дефекты, в то время как для контактных или проекционных фотошаблонов это приводит к браку. Другое применение голограммы в технологии – использование ее в качестве линзы. Фокусирующие свойства зонных решеток известны давно. Однако применение решеток ограничивалось трудностями их изготовления. Голографические зонные решетки – голограммы точечного источника – просты в изготовлении и несомненно будут полезны в лазерной технологии. Например, с помощью голографических линз получали отверстия диаметром до 14 мкм в танталовой пленке, нанесенной на стекло. Голографические решетки совсем не имеют ошибок, свойственных обычным решеткам, нарезанным на делительной машине. ЗАКЛЮЧЕНИЕ В качестве заключения также необходимо указать, что наряду с рядом практических задач, решенных методами голографической проекции, существует целый спектр проблем, решение которых методами голографии является задачей будущего. В основном это связано, что общая картина этого явления пока еще далека от завершения. И дело здесь не только в том, что в ряде случаев мы не знаем полностью набор отображающих свойств некоторых видов голограмм. Есть все основания считать, что будут открыты новые неожиданные оптические свойства голограмм. Вполне вероятно, что ряд новых эффектов будет обнаружен при применении светочувствительных материалов, обладающих специфическими свойствами, подобно тому, как применение резонансных и поляризационных сред открыло возможность записи временных и поляризационных характеристик волновых полей. И наконец, прецедент объединения голографии и нелинейной оптики в динамическую голографию показывает, что внесение идей голографии в смежные с ней области знаний может привести к появлению совершенно новых направлений. СПИСОК ЛИТЕРАТУРЫ 1. П.В. Короленко. «Оптика когерентного излучения». Москва, 1997. 2. Сороко Л.М. «Основы голографии и когерентной оптики».- М.: Наука, 1971. 3. Парыгин В.Н., Балакший В.И. «Оптическая обработка информации».- М.: Изд. МГУ, 1987. 4. М.Борн и Э.Вольф "Основы оптики". 5. А.С. Башкин, В.В. Лобачев, И.А. Федоров "Анализ пространственных масштабов оптических неоднородностей в активных средах мощных проточных лазерных усилителей", "Квантовая электроника", 24, 2 (1997), с.173-175 |
