РГЗ. Интерференция Теоретические сведения
 Скачать 185 Kb.
|
|
Интерференция Теоретические сведения. Рассмотрим интерференционную картину, получаемую от пластинок переменной толщины (от клина). Направления распространения световой волны, отраженной от верхней и нижней границы клина, не совпадают. Отраженные и преломленные лучи встречаются, поэтому интерференционную картину при отражении от клина можно наблюдать и без использования линзы, если поместить экран в плоскость точек пересечения лучей (хрусталик глаза помещают в нужную плоскость). Интерференция будет наблюдаться только во 2-й области клина, так как в 1-й области оптическая разность хода будет больше длины когерентности. Результат интерференции в точках P1 и P2 экрана определяется по известной формуле  , подставляя в неё толщину пленки в месте падения луча (b1 или b2). Свет обязательно должен быть параллельным ( ): если одновременно будут изменяться два параметра b и α, то устойчивой интерференционной картины не будет.Поскольку разность хода лучей, отразившихся от различных участков клина, будет неодинаковой, освещенность экрана будет неравномерной, на экране будут темные и светлые полосы (или цветные при освещении белым светом, как показано на рисунке). Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины. Задание. На прозрачный клин, показатель преломления которого равен n=1,49, нормально к его грани падает монохроматический свет с длиной волны λ. Клин находится в воздухе; преломляющий угол клина α=6,0·10-4 рад. Толщина клина в том месте, где наблюдается k=1 интерференционная полоса, равна dk. Расстояние между соседними интерференционными линиями b=0,33 мм. Найти λ. Решение. 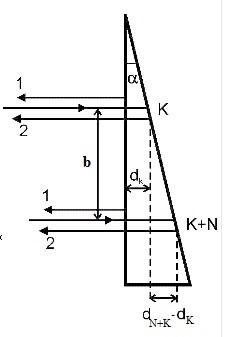 Так как интерференционные полосы наблюдаются при малом угле α клина, то отраженные лучи 1 и 2 будут фактически параллельными. Светлые полосы наблюдаются на тех участках клина, для которых оптическая разность хода равна четному числу длин полуволн:  Разность хода двух лучей 1 и 2 при нормальном падении света равна:   - добавочная разность хода, возникающая при отражении волны от оптически более плотной среды.Тогда получим:  Аналогично получаем: 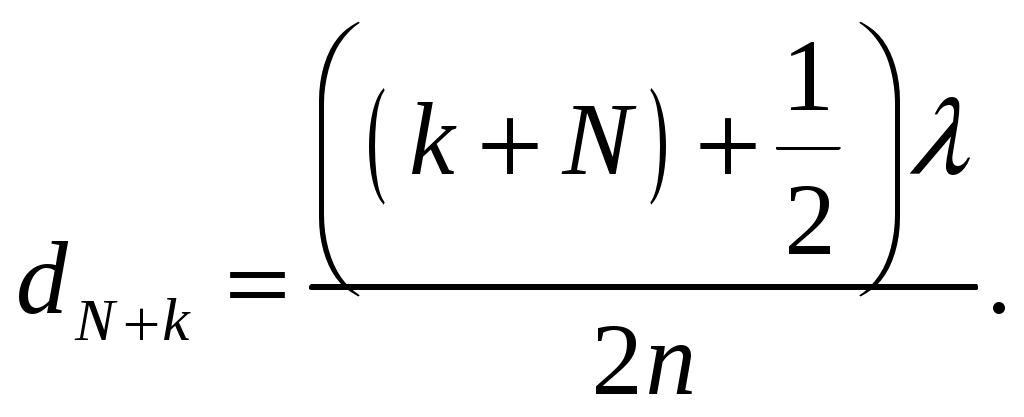 Ввиду малости угла α можно считать, что  Поэтому из треугольника получаем:  Так как b есть расстояние между соседними минимума, то  Тогда:  Ответ: λ=590 нм. Дифракция Теоретические сведения. Простейшая дифракционная решетка состоит из прозрачных участков (щелей), разделенных непрозрачными промежутками. На решетку с помощью коллиматора направляется параллельный пучок исследуемого света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой. 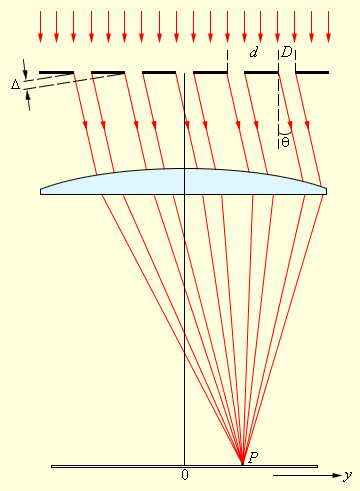 В каждой точке P на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под определенным углом θ к направлению падающей волны. Колебание в точке P является результатом интерференции вторичных волн, приходящих в эту точку от разных щелей. Для того, чтобы в точке P наблюдался интерференционный максимум, разность хода Δ между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн:  Здесь d – период решетки, m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины. Задание. На пропускающую дифракционную решетку с периодом d падает нормально монохроматический свет с длиной волны λ. На экране, расположенном за собирающей линзой параллельно решетке и отстоящем от нее на расстояние L=2 м, наблюдается дифракционная картина. Расстояние между двумя дифракционными максимума k= -2 иi=3 порядков равноl=10см. Период решетки равен d=30 мкм. Найти λ, mmax(число главных максимумов), n (число штрихов на миллиметр длины), N- число штрихов на микрометр длины. Решение.  Для решения задачи воспользуемся уравнением Брэгга-Вульфа. Запишем его для двух порядков максимумов:  Выразим из уравнений постоянную решетки и приравняем оба выражения:  Так как углы дифракции малы, то синусы можно заменить тангенсами:  Из рисунка найдем тангенсы соответствующих углов:  Вернемся к соотношению тангенсов: 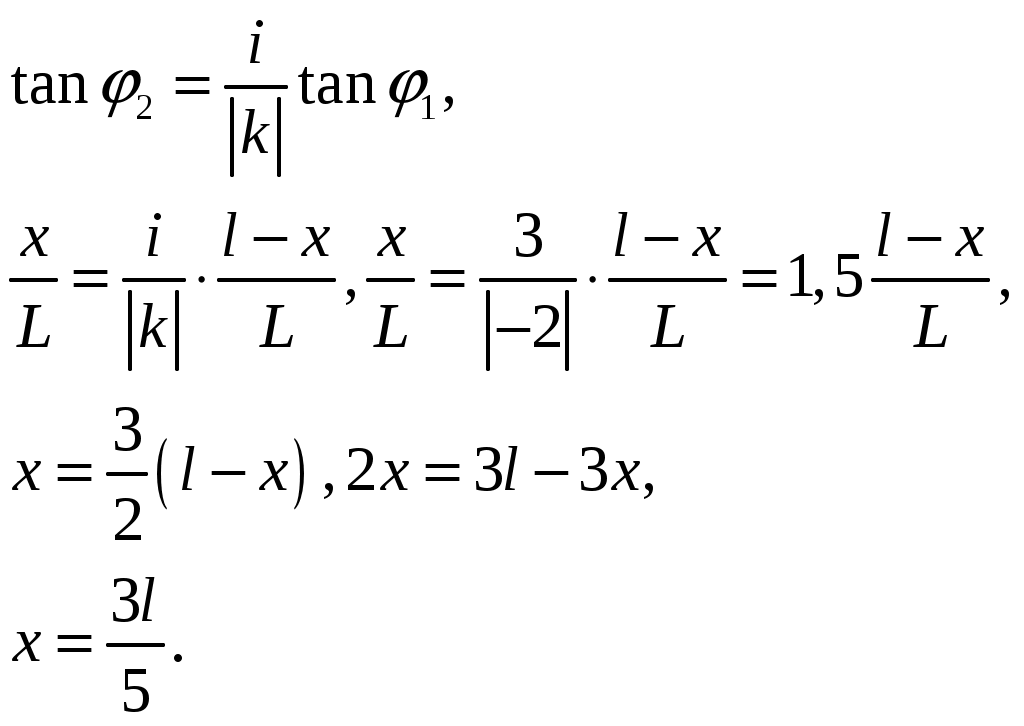 Теперь находим длину волны: 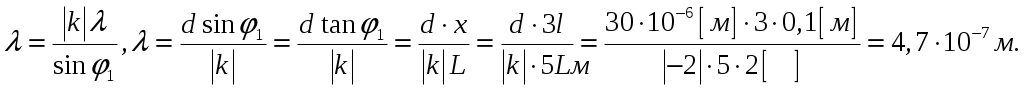 Для определения общего числа главных максимумов, даваемых дифракционной решеткой, исходим из условия, что максимальный угол отклонения лучей от нормального направления распространения не может превышать 90°, т.е.:  По определению постоянной решетки имеем, что период решетки есть величина, обратная числу штрихов на единицу длину (в частности на метр), тогда имеем:  Число штрихов на метр длины больше на 1000, поэтому:  Ответ:  Распределение интенсивности имеем вид, показанный на рисунке.  Поляризация Теоретические сведения. Рассмотрим прохождение естественного света последовательно через два идеальных поляроида Р и А, разрешенные направления которых развернуты на некоторый угол φ. Первый поляроид играет роль поляризатора. Он превращает естественный свет в линейно-поляризованный. Второй поляроид служит для анализа падающего на него света. Здесь также используется явление дихроизма. Световую волну с амплитудой E0 разложим на две составляющие.  закон Малюса:  В естественном свете все значения φ равновероятны. Поэтому интенсивность естественного света, прошедшего один поляризатор уменьшается в два раза. Поставим на пути естественного света два поляризатора, плоскости которых образуют угол φ. Из первого поляризатора выйдет луч интенсивностью  . Согласно закону Малюса интенсивность света, прошедшего второй поляризатор равна: Задание. Плоская неполяризованная волна интенсивностью I0 падает на систему из N=2 поляризаторов. Главные сечения поляризаторов относительно друг друга повернуты на угол α1=45°. Потери интенсивности света вследствие отражения и поглощения в каждом поляризаторе составляют k. Интенсивность света, прошедшего через оптическую систему, равна I=0,24I0. Найти k. Решение.  Воспользуемся законом Малюса. После прохождения света через первый поляризатор интенсивность света (с учетом отражения и поглощения) составит:  Поле прохождения второго поляризатора получим:  Так как известна интенсивность прошедшего света, то получим:  Находим искомый коэффициент: 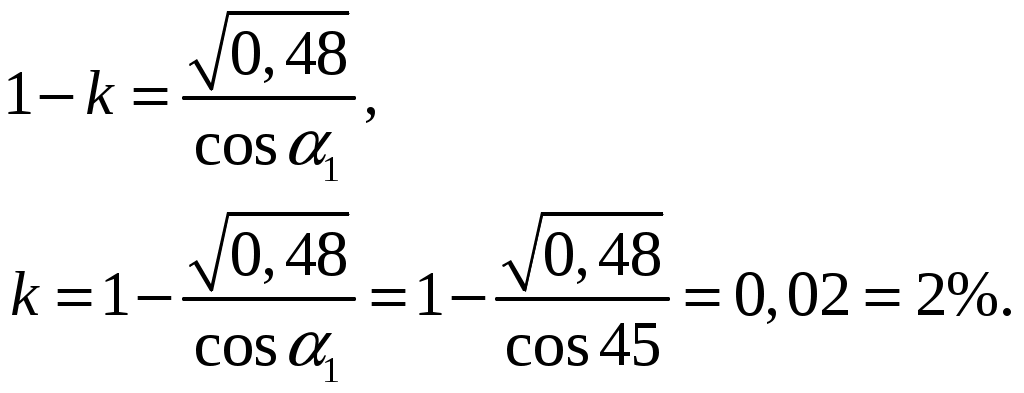 Ответ: k=2%. |