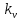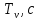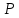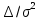Доп. главы математики. ДГМ_1_3в_5403_ГалееваАР. Формирование случайных сигналов с заданными вероятностными характеристиками
 Скачать 198.78 Kb. Скачать 198.78 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра РАПС отчЁт по практической работе № 1 по дисциплине «Дополнительные главы математики» Тема: Формирование случайных сигналов с заданными вероятностными характеристиками
Санкт-Петербург 2020 Цель работы: получение практических навыков формирования случайных сигналов с требуемыми вероятностными характеристиками. Таблица 1 – Исходные данные
Постановка задачи В работе требуется инструментальными средствами Simulink сформировать случайный процесс 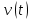 , имеющие наперёд заданные статистические характеристики, соответствующие спектральной плотности вида , имеющие наперёд заданные статистические характеристики, соответствующие спектральной плотности вида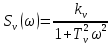 Для сформированного случайного процесса определить требуемый объём экспериментальных значений (выборки) и необходимое время моделирования, для которых доверительный интервал шириной ∆ будет накрывать истинное значение его дисперсии с заданным уровнем вероятности Р. Конкретные значения уровней вероятности Р и ∆ задаются в табл.1, где обозначено 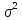 – истинное значение дисперсии. – истинное значение дисперсии.Используя графические примитивы Simulink реализовать модель, состоящую из генератора белого шума, фильтра первого порядка с параметрами, обеспечивающими требуемый уровень спектральной плотности на его выходе, и устройства для оценки значений среднего и дисперсии формируемого сигнала. Для оценки среднего и дисперсии по выборке конечной длины использовать следующие выражения: 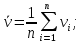 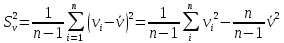 Путём модельного эксперимента определить оценку значения 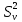 и ширину доверительного интервала, накрывающего истинное значение дисперсии с заданной вероятностью. Сравнить величину оценки дисперсии, полученной экспериментальным путём, с её расчётным значением, рассчитанным по формуле: и ширину доверительного интервала, накрывающего истинное значение дисперсии с заданной вероятностью. Сравнить величину оценки дисперсии, полученной экспериментальным путём, с её расчётным значением, рассчитанным по формуле: 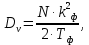 где обозначено: 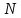 – уровень интенсивности генератора белого шума; – уровень интенсивности генератора белого шума; 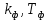 – соответственно коэффициент передачи и постоянная времени формирующего фильтра. – соответственно коэффициент передачи и постоянная времени формирующего фильтра.Построим модель, включающую в себя генератор белого шума, формирующий фильтр и две подсистемы для измерения оценок значения среднего и дисперсии сигнала на входе и выходе формирующего фильтра (рис.1 и рис.2). 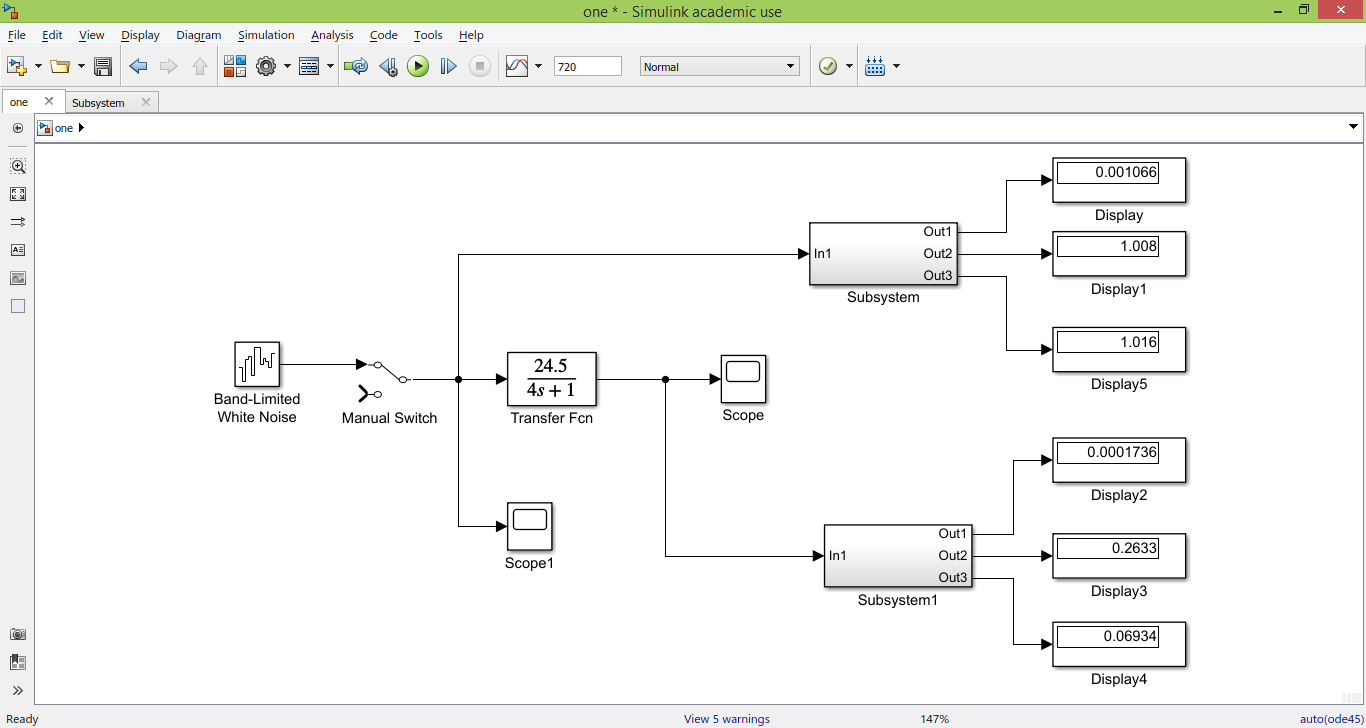 Рисунок 1 – Схема модели 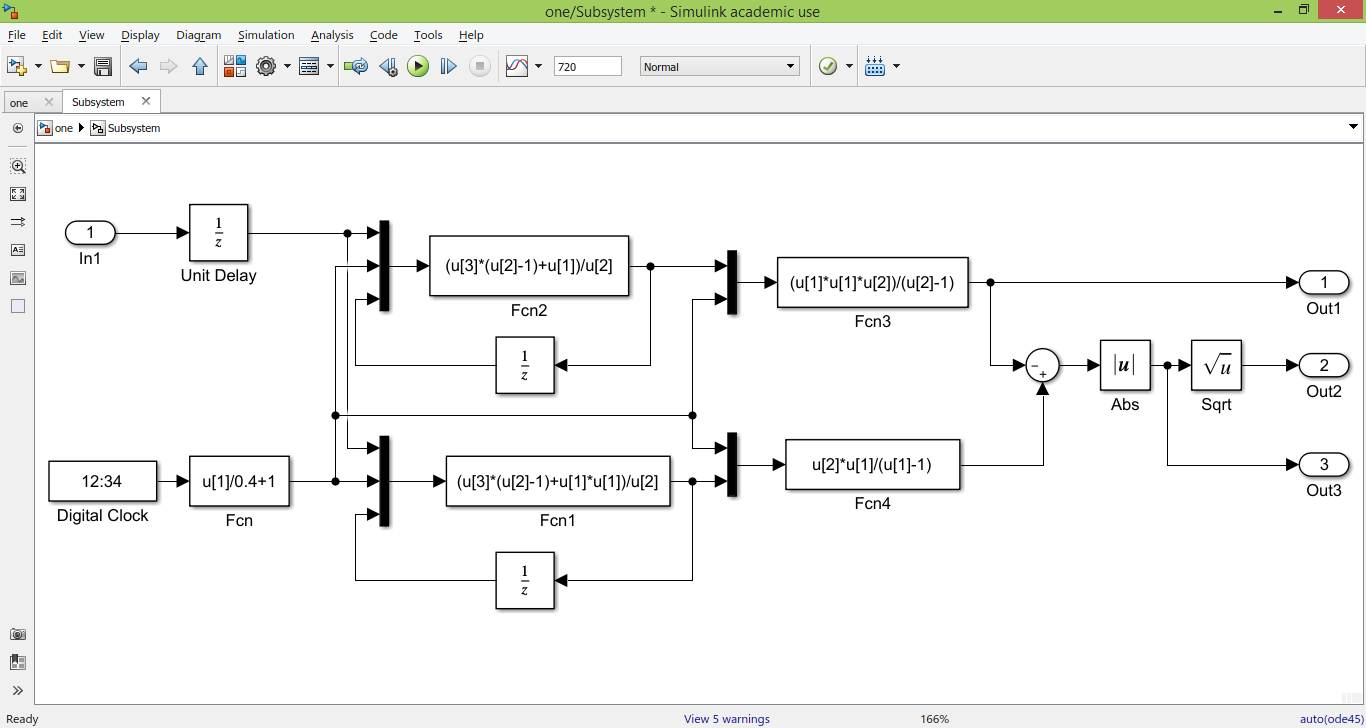 Рисунок 2 – Схема блока Subsystem Рассчитаем коэффициент передачи формирующего фильтра и постоянную времени: 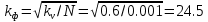 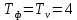 С целью получения интервальных оценок дисперсии с заданной вероятностью 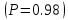 и заданной шириной доверительного интервала и заданной шириной доверительного интервала 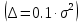 , необходимо определить необходимый для этого объём выборки. В моем случае выражение для расчёта требуемого объёма выборки получит вид: , необходимо определить необходимый для этого объём выборки. В моем случае выражение для расчёта требуемого объёма выборки получит вид: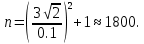 Период дискретизации экспериментальных точек в этом случае может быть выбран равным: 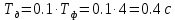 . Следовательно, модельное время необходимо установить равным . Следовательно, модельное время необходимо установить равным 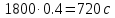 . .В результате моделирования величина дисперсии составляет 0.06934. Вычислим теоретическое значение дисперсии на выходе фильтра первого порядка: 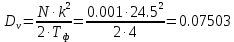 Вывод: В ходе работы мы построили модель для получения цветного шума из генератора белого шума с помощью фильтра в MATLAB. Также получены параметры входного сигнала: среднего значения 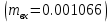 , и дисперсия , и дисперсия 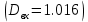 , что соответствует параметрам белого шума , что соответствует параметрам белого шума 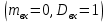 . А так же была получена дисперсия выходного сигнала . А так же была получена дисперсия выходного сигнала 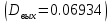 и она соответствует теоретическому значению дисперсии и она соответствует теоретическому значению дисперсии 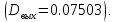 |