кейс по математике. Кейс Показательная функция. Формула сложных процентов и логарифмы
 Скачать 275.5 Kb.
|
|
МБОУ «ОКТЯБРЬСКАЯ СРЕДНЯЯ ШКОЛА» Кейс «Численность популяции» (используется на этапе закрепления изученного по теме ) Автор: учитель математики Волик Т.Г. Класс: 10 Тема: «Формула сложных процентов и логарифмы» Временные рамки: 40 мин Цель кейса: применение знаний по теме «Формула сложных процентов и логарифмы» для решения задач экологической направленности. Ознакомьтесь с предложенным текстом. Математика – царица всех наук. Как часто мы слышим эти слова, сказанные немецким математиком Карлом Гауссом (1777-1855) много лет назад. Современный мир неожиданно обнаружил, что математика уверенно расположилась в самых разных его частях и уголках. Сейчас никого не удивишь словосочетаниями "математическая лингвистика", "математическая биология", "математическая экономика" и т.п. — какую дисциплину ни взять, вряд ли кому-нибудь покажется невозможным присоединение к ее наименованию эпитета "математический". Математика занимает сегодня видное место в жизни общества. Рост количества бактерий, концентрация адреналина в крови, способность почек выводить из крови радиоактивные изотопы, восстановление концентрации гемоглобина в крови, рост количества древесины, количество радиоактивного вещества, изменение количества населения – все это измеряется по законам показательной функции. В жизни нередко приходиться встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине. В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид y=y0ax Для решения биологических задач можно использовать формулу сложных процентов  которая может привести к вычислению значений логарифмов.2. Выполните задание: 1)Численность популяции составляет 5 тыс. особей. За последнее время в силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида? Предположите, через сколько лет это произойдет? Решите задачу, используя формулу сложных процентов. 2) Совпало ли ваше предположение с действительностью? Примерное содержание ответов: Решение:Применим для вычисления времени формулу сложных процентов: 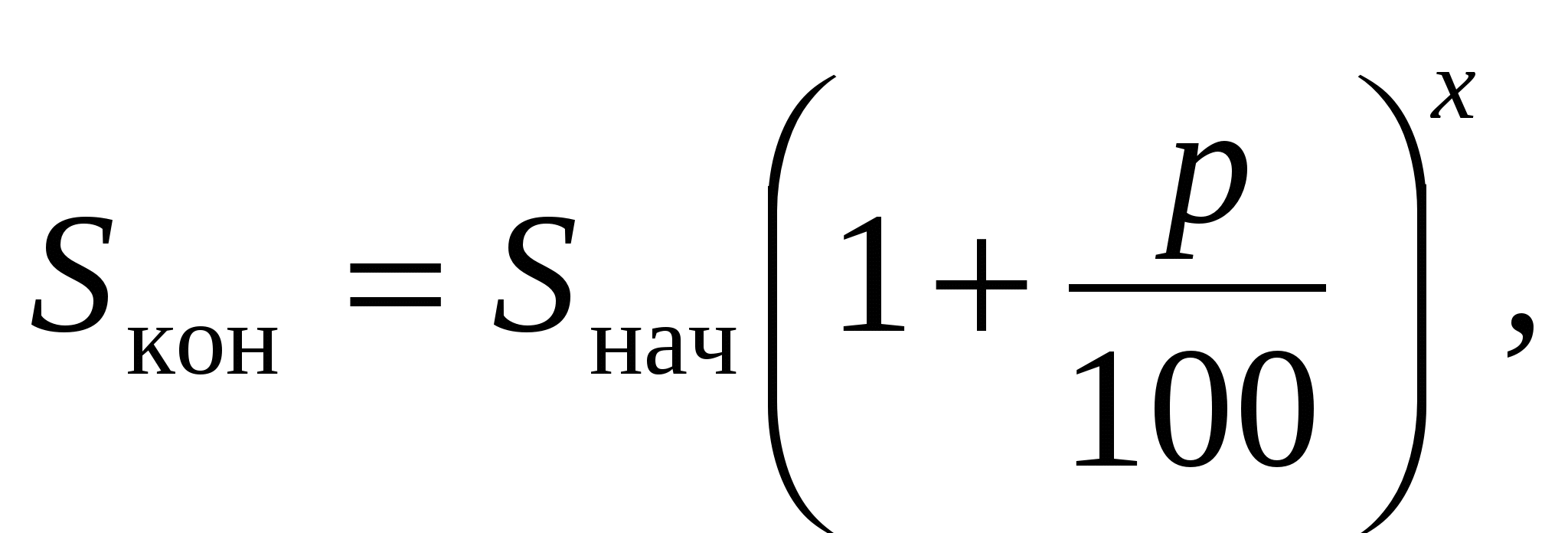где 2 тыс. – численность животных по истечению искомого времени; 5 тыс. – численность животных в начальный момент времени;p =8 - % сокращения численности животных. Предварительно разделив обе части уравнения на 1000, получим: 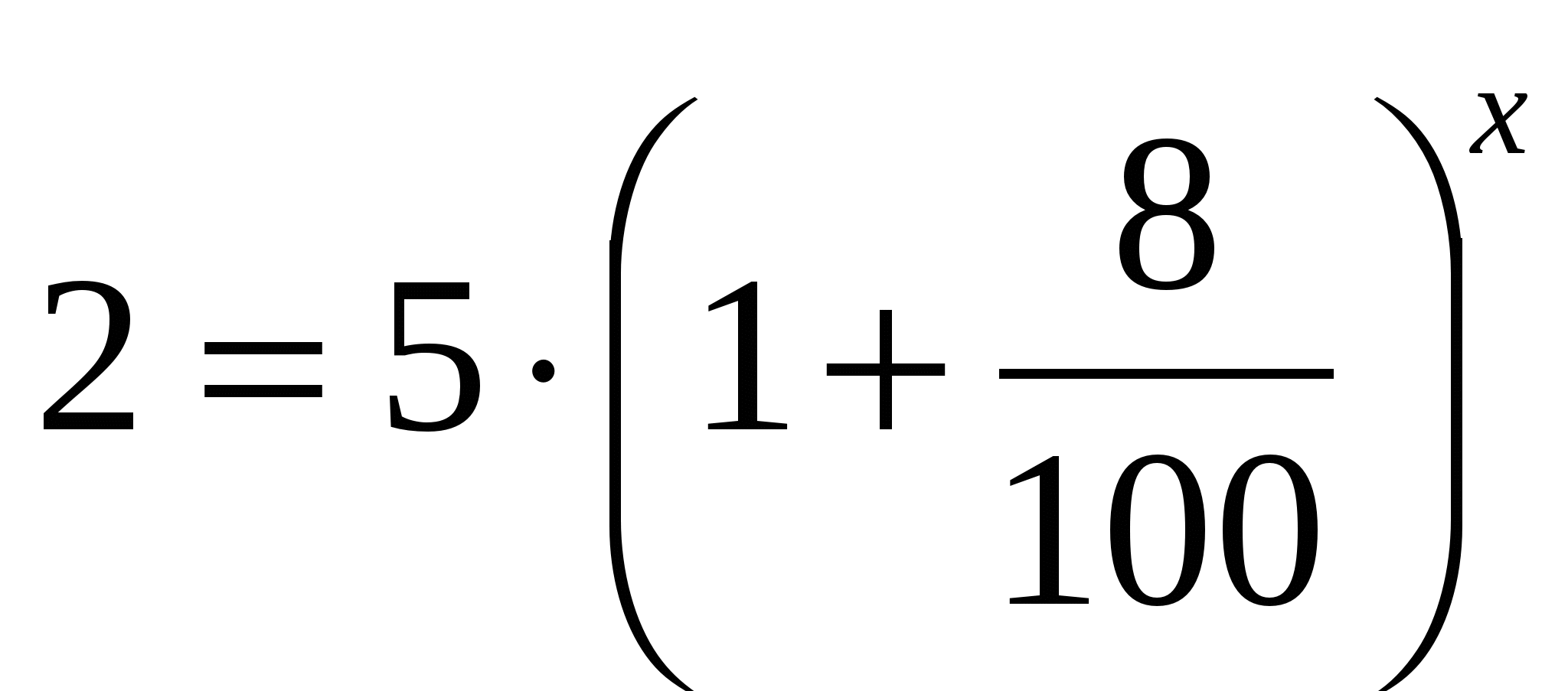 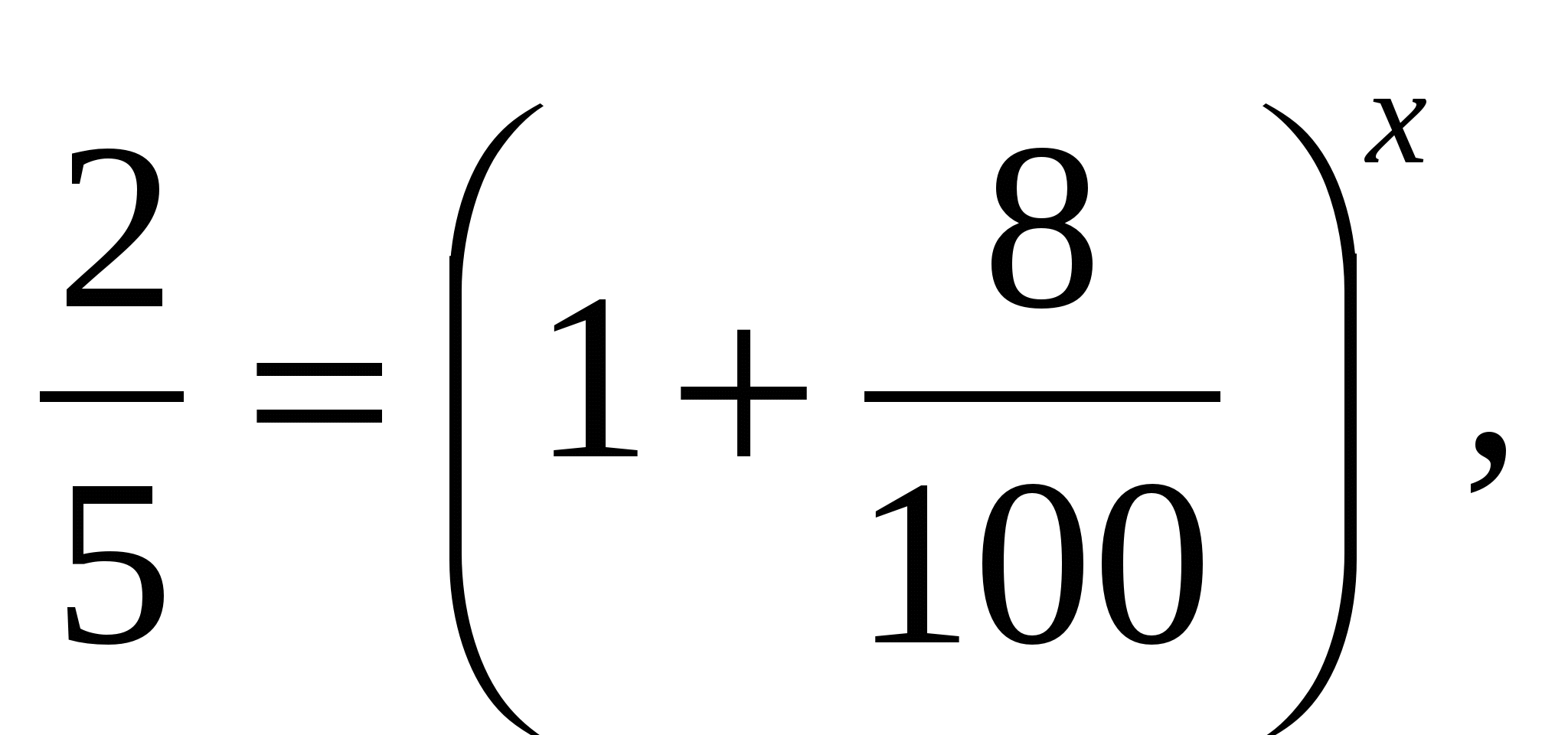   лет.Ответ: Приблизительно через 11 лет. |