Новый документ. Формулировка и доказательство теоремы косинусов

• Название: Формулировка и доказательство теоремы косинусов
• Дата: 24.07.2022
• Размер: 42.62 Kb.
• Имя файла: Новый документ.docx
• Тип: Документы; #635344

Формулировка и доказательство теоремы косинусов

Теорема косинусов является обобщением теоремы Пифагора для произвольного треугольника.

Формулировка теоремы косинусов

Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение: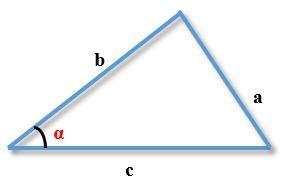

Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними

Полезные формулы теоремы косинусов: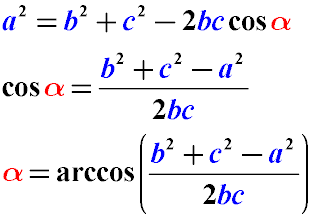



Как видно из указанного выше, с помощью теоремы косинусов можно найти не только сторону треугольника по двум сторонам и углу между ними, можно, зная размеры всех сторон треугольника, определить косинусы всех углов, а также вычислить величину любого угла треугольника. Вычисление любого угла треугольника по его сторонам является следствием преобразования формулы теоремы косинусов.

Доказательство теоремы косинусов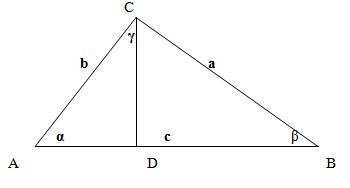

Рассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)

Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD.

Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что

AB = AD + BD

Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике:

AD / AC = cos α

откуда

AD = AC cos α

AD = b cos α

Длину стороны BD найдем как разность AB и AD:

BD = AB - AD

BD = c − b cos α

Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

для треугольника BDC

CD² + BD² = BC²

для треугольника ADC

CD² + AD² = AC²

Обратим внимание на то, что оба треугольника имеют общую сторону - CD. Определим ее длину для каждого треугольника - вынесем ее значение в левую часть выражения, а остальное - в правую.

CD² = BC² - BD²

CD² = AC² - AD²

Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений:

BC² - BD² = AC² - AD²

Исходя из сделанных ранее вычислений, мы уже знаем что:

AD = b cos α

BD = c − b cos α

AC = b (по условию)

А значение стороны BC обозначим как a.

BC = a

(Именно его нам и нужно найти)

Получим:

BC² - BD² = AC² - AD²

Заменим буквенные обозначения сторон на результаты наших вычислений

a² - ( c − b cos α )² = b² - ( b cos α )²

перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения - на правую

a² = ( c − b cos α )² + b² - ( b cos α )²

раскроем скобки

a² = b² + c ² - 2c b cos α + ( b cos α )² - ( b cos α )²

получаем

a² = b² + c ² - 2bc cos α

Теорема косинусов доказана.

Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.

Теорема синусов

Теорема синусов устанавливает зависимость между величиной углов треугольника и противолежащих ему сторон.
Формулировка теоремы синусов:

Стороны треугольника пропорциональны синусам противолежащих углов
или,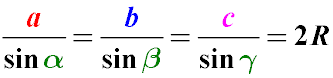

где

R - радиус описанной вокруг треугольника окружности

a, b, c - стороны треугольника

α, β, γ - величины противолежащих этим сторонам углов

Доказательство теоремы синусов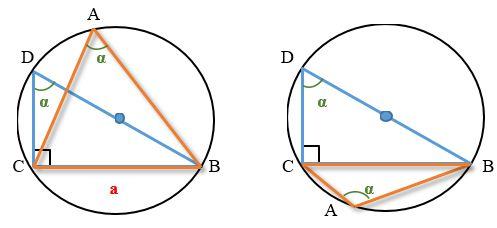

Доказательство теоремы синусов происходит с помощью дополнительных построений.
Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.

Дополнительно построим диаметр окружности, в который вписан произвольный треугольник, но так, чтобы он проходил через один из его углов. Диаметр равен двойному радиусу окружности (2R).
Примем во внимание, что одним из свойств прямоугольного треугольника, вписанного в окружность является то, что его гипотенуза, является диаметром окружности, в которую он вписан.
Обозначим диаметр для описанной окружности как BD. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность).
Таким образом, дополнительно построенный треугольник, у которого одна общая сторона с построенным ранее произвольным треугольником, а гипотенуза совпадает с диаметром окружности - является прямоугольным. То есть треугольник DBC - прямоугольный.

Для доказательства всей теоремы, поскольку размеры треугольника ABC выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R.
Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.
Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π - CAB (в противном случае).
Обратимся к свойствам тригонометрических функций. Поскольку sin( π − α ) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.
Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника.
2R = BC / sin A

2R = BC / ( BC / DB )

2R = DB
А, поскольку, DB строился как диаметр окружности, то равенство выполняется.

Повторив то же рассуждение для двух других сторон треугольника, получаем: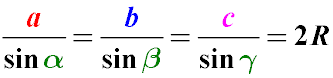

Теорема синусов доказана.