ргр вариант 1-2. Формулировка задания исследование 1
 Скачать 67.43 Kb. Скачать 67.43 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное агентство по образованию ГОУ ВПО «Магнитогорский государственный технический университет им. Г.И.Носова» Кафедра химической технологии неметаллических материалов и физической химии РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 1 По курсу «Физическая химия» раздел «Термодинамика» вариант 1-2 Выполнил: Студент гр. МСЭ-10 Айменов Н.К. Проверил: Доц., канд. техн. наук Смирнов A.H. 1.ФОРМУЛИРОВКА ЗАДАНИЯ Исследование 1 Дана реакции 2AlCl₃+3H₂=2Al+6HCl . Выполнить следующее:
Исследование 2
а) увеличении давления (постоянная температура ); б) увеличении температуры (постоянное давление). 3.1. Исследование 1 Таблица 2 Исходные данные для термодинамического исследования реакции 2AlCl₃+3H₂=2Al+6HCl
3.1.1. Расчет изменения изобарной теплоемкости ∆Сp и теплового эффекта реакции ∆Н⁰т Зависимость теплового эффекта реакции от температуры определяется законом Кирхгофа ∆Н⁰т = ∆Н⁰₂₉₈ + ∆CpdT , (1) где ∆Н⁰₂₉₈ - стандартный тепловой эффект реакции при 298 К; ∆Cp - изменение теплоемкости системы в результате протекания реакции. Последняя величина рассчитывается по уравнению ∆Cp = Σ(niCp,i) кон –Σ(niCp,i) исх , (2) Где Cp,i- мольная изобарная теплоемкость i-го вещества определяемая из уравнения Сp,i = ai + biT + ci’T⁻² (3) ni - стехиометрический коэффициент i-го вещества в уравнении реакции. Для исследуемой реакции, после подстановки в уравнение (2) ni , оно примет вид ∆Cp=(6 Cp + 2Cp )-(2 Cp + 3 Cp ) (4) Определим температурные зависимости Сp,i для всех реагентов, используя уравнение (2) и термодинамические данные в табл. 2: Cp =55,44+117,15∙10⁻³T; (5a) Cp =27,28+3,26∙10⁻³Т+0,5∙10⁵Т⁻² (5b) Cp =20,67+2,39∙10⁻³Т (5с) Cp =28,05+3,52∙10⁻³Т (5d) Определим расчетные уравнения ∆Cp = f(T) для исследуемой реакции. Для чего подставим уравнения (5а, 5b, 5c и 5d) в уравнение (4). После подстановки получим ∆Cp=[6(28,05+3,52∙10⁻³Т)+2(20,67+2,39∙10⁻³Т)]-[2(55,44+117,15∙10⁻³Т)+3(27,28+3,26∙10⁻³Т+0,5∙10⁵Т⁻²)] = 16,92-218,18∙10⁻³-1,5∙10⁵T⁻². Рассчитаем значение ∆Cp при различных температурах и сведем эти значения в табл. 3. При шаге по температуре в 20 К необходимо рассчитать ∆Cp при следующих температурах: 300, 320, 340, 360, 380, 400, 420 и 440 К. Таблица 3 Величина ∆Cp при различных температурах для реакции 2AlCl₃ + 3H₂ = 2Al + 6HCl
По данным табл. 3. Строим зависимость ∆Cp=f(T) , как на рис.1. Рис. 1. Зависимость изменения изобарной теплоемкости от температуры Значение ∆Н⁰₂₉₈ в уравнении (1) определяется по стандартным теплотам образования ∆Н⁰₂₉₈‚i ∆Н⁰₂₉₈ = Σ(niH⁰₂₉₈ i )кон – Σ(niH⁰₂₉₈,i )исх (7) В рассматриваемом случае уравнение (7) имеет вид ∆Н⁰₂₉₈ = (6∆Н ₂₉₈ + 2∆Н ₂₉₈) – (2∆Н ₂₉₈ + 3∆Н⁰₂₉₈) (8) или в числовом виде ∆Н⁰₂₉₈ = (-96,46∙6-2∙0)-(-697,4∙2) = -578,76+1394,8 = 816040 Дж. Чтобы в дальнейшем избежать ошибки при расчете ∆Н⁰т, необходимо теплоты образования реагентов в табл. 2 из килоджоулей перевести в джоули. В соответствии с заданием необходимо рассчитать тепловые эффекты в интервале температур 300-440 К. То есть для исследуемой реакции, в интервале температур 300-440 К, после подстановки численных значений ∆Н⁰₂₉₈ и уравнения (6) в уравнение (1), получим уравнение зависимости теплового эффекта для первой реакции от температуры: ∆Н⁰ = ∆Н⁰₂₉₈ + 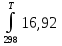 dT - dT - 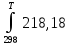 ∙10⁻³TdT- ∙10⁻³TdT-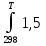 ∙10⁵T⁻²dT = ∙10⁵T⁻²dT = 816040+16,92(Т-298)- 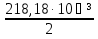 (Т²-298²)+1,5∙10⁵( (Т²-298²)+1,5∙10⁵(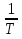 - -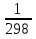 ). (9) ). (9)После подстановки значений температур в уравнение (9) получим тепловые эффекты, значения которых сведем в табл. 4. Таблица 4 Величина ∆Н⁰ при различных температурах для реакции 2AlCl₃₍тв₎ + 3H₂₍г₎ = 2Al₍тв₎+6HCl₍г₎
Зависимость ∆Н⁰Т = f(T), построенная по данным табл. 3, представлена на рис. 2. Рис. 2. Зависимость теплового эффекта реакции 2AlCl₃+3H₂=2Al+6HCl от температуры tgα = ∆C⁰i,₃₆₀ = 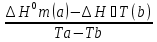 = = 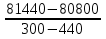 = - 4,5Дж/К. = - 4,5Дж/К.3.1.2. Расчет изменения энтропии реакции Изменение энтропии системы в результате протекания процесса определяется по уравнению ∆S⁰т = ∆S⁰₂₉₈ + 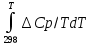 . (10) . (10)В этом уравнении ∆S⁰₂₉₈ - стандартное изменение энтропии для реакции при 298 К, определяемое по мольным стандартным энтропиям веществ S⁰₂₉₈,i ∆S⁰₂₉₈ = Σ(ni S⁰₂₉₈,i )кон - Σ(ni S⁰₂₉₈,i )исх. (11) Значения S⁰₂₉₈,i для соответствующих веществ приведены в табл. 1, после их подстановки в уравнение (11) получим ∆S⁰₂₉₈ = (6S₂₉₈ + 2S₂₉₈ )-(2S₂₉₈ + 3S₂₉₈ ) = 445,62 Дж/К. ∆S⁰т = ∆S⁰₂₉₈ + 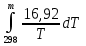 - - 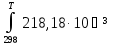 dT - dT - 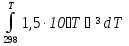 = = 445,62 + 16,92 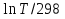 – 218,18·10⁻³(T-298) + – 218,18·10⁻³(T-298) + 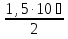 ( (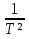 - - 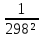 ). (12) ). (12)Рассчитаем по этому уравнению изменения энтропии для температур 300, 320, 340, 360, 380, 400, 420 и 440 К, а результат сведем в табл. 5. Таблица 5 Величина ∆S⁰т при различных температурах для реакции 2AlCl₃ + 3H₂ = 2Al + 6HCl
По данным табл. 5 построим зависимость ∆S⁰т = f(T) (рис. 3). Рис. 3. Зависимость изменения энтропии от температуры 3.1.3. Расчет изменения стандартной энергии Гиббса При расчете изменения стандартной энергии Гиббса для реакции воспользуемся уравнением Гиббса-Гельмгольца ∆G⁰T = ∆H⁰т - T∆S⁰т. (13) Найденные по уравнению (13) величины изменения стандартной энергии Гиббса приведены в табл. 6, по данным которой построена зависимость ∆G⁰т = f(T), изображенная на рис. 4. Таблица 6 Значения изменения стандартной энергии Гиббса ∆G⁰т при различных температурах
По данным табл. 6 построим зависимость ∆G⁰т = f(T) (рис. 4). Рис. 4. Зависимость изменения стандартной энергии Гиббса от температуры 3.1.4. Вывод уравнения зависимости константы равновесия от температуры Константа равновесия связана с изменением стандартной энергии Гиббса соотношением lnKp = - 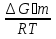 . (14) . (14)После подстановки выражения (13) в уравнение (14) получим lnKp = - 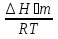 + + 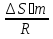 . (15) . (15)Можно полагать, что в сравнительно небольшом интервале температур для исследуемой в данном примере реакции тепловой эффект реакции ∆Н⁰т и изменение энтропии ∆S⁰т практически постоянны величины. Отсюда уравнение (15) можно записать в виде lnKp = (A/T)+B, (16) где А и В – постоянные, которые соответственно равны: А = -∆Н⁰т/R; (17) B = ∆S⁰т/R. (18) Уравнение (16) отвечает линейной зависимости lnKp = f(1/T). В табл. 1, графа 8 предлагается определить эту зависимость для температурного интервала 300-440 К. Для построения зависимости lnKp = f(1/T) определим lnKp из уравнения (14) и сведем полученные данные в табл. 7. Таблица 7 Величины констант равновесия при различных температурах
Для графического определения констант А и В в уравнении (16) по данным табл. 7 строим зависимость lnKp = f(1/T), приведенной на рис. 5. Рис. 5. Зависимость lnKp от обратной температуры для реакции 2AlCl₃ + 3H₂ = 2Al + 6HCl График на рис. 5 представляет собой прямую, тангенс угла которой к оси абсцисс численно равен коэффициенту А в уравнении (16). Для нахождения величины тангенса возьмем на прямой, как это показано на рис. 5, произвольно две точки а и b и определим численные значения их ординат и абсцисс. Можно записать А = tgα = 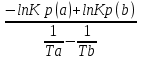 = = 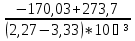 = -97800. = -97800.Для определения численного значения В поступим следующим образом. Из табл. 7 возьмем значение lnKp при 1000/Т = 2,27 (lnKp = 170), подставим его вместе с численным коэффициента А, найденным ранее, в уравнение (16), которое предварительно выразим через В. B= lnKp - А·1/Т = 170,03-(-97800·0,00227) = 51,976. Итак, приближенное уравнение зависимости константы равновесия от температуры имеет вид lnKp = -97800/Т + 51,976. (19) Последнее уравнение позволяет рассчитать значение Кр при любой температуре, если последняя находится в заданном интервале (т.е. 300-440). По значениям коэффициентов А и В рассчитаем величину среднего теплового эффекта реакции -∆Н⁰т и изменения энтропии -∆S⁰т. Согласно уравнениям (17)-(18) имеем: ∆Н⁰т= -А·R = 97800·8,31 = 812718 Дж; ∆S⁰т = B·R = 51,976·8,31 = 431,9 Дж/К. Полученные данные неплохо согласуются с данными, приведенными в табл. 3 и 4, что указывает на правильность расчетов. 3.2. Исследование 2 3.2.1. Определение числа фаз, независимых компонентов и степеней свободы Рассматриваемая система состоит из трех фаз: двух твердых фаз AlCl₃ и Al, а также одной газообразной, представляющей смесь газов H₂ и HCl. Итак, ф=3. Число независимых компонентов k равно наименьшему числу веществ, необходимых для выражения состава всех фаз системы. Это число определяется как общее число веществ в системе m за вычетом числа связей между ними r. Связь между веществами в рассматриваемую систему, выражается уравнением реакции. Следовательно, k = m – r = 4-1 = 3. (20) Число степеней свободы равно числу параметров системы ( давления, температуры, концентрации компонентов), которые можно изменить в некоторых пределах так, чтобы число и природа фаз оставались прежними. По правилу фаз Гиббса С = k + n – ф, (21) Где n – число внешних параметров, влияющих на состояние равновесия системы. Обычно это давление и температура, т.е. n = 2. Для рассматриваемой системы c = k + 2 –ф = 3 + 2 – 3 = 2. Если в качестве независимых переменных выбрать давление Р и температуру Т, то концентрации HСl и Н₂ в состоянии равновесия будут функциями этих переменных. Например, %НСl = f(P, T). 3.2.2. Определение возможного направления реакции Дл решения этой задачи воспользуемся уравнением изотермы Вант-Гоффа ∆G = RT(lnПр – lnKp) . (22) Где Пр – произведение фактических парциальных давлений газовых компонентов реакции; Kp – константа равновесия реакции при данной температуре. Напоминаю, что в соответствии со вторым законом термодинамики в изобарно-изотермических условиях возможны самопроизвольные протекания процессов, сопровождающихся уменьшением энергии Гиббса системы ∆G < 0. (23) В применении к химической реакции это означает, что процесс самопроизвольно может идти слева направо при ∆G < 0 и справа налево при ∆G > 0. Из уравнения (18) следует, что первое условие (∆G < 0) выполняется при Пр < Kp, а второе (∆G > 0) – при Пр > Kp. Таким образом, для ответа на поставленный вопрос необходимо рассчитать константу равновесия при заданной температуре (Т = 500К) и величину Пр при содержании Н₂ равном 50% об. и НСl – 50% об., а также общем давлении, равном 103,3 кПа. Найдем величину Kp при 500 К из выведенного в п. 3.1.4 уравнения (19) ln Kp,500= -97800/T + 51,976 = -97800/500 + 51,976 = -143,62. Отсюда Kp,500 = е⁻¹⁴³·⁶² =4,23. В соответствии с уравнением реакции 2AlCl₃ + 3H₂ = 2Al + 6HCl произведение фактических парциальных давлений запишется Пр = (Р’НСl)⁶ /(Р’Н₂)³, (24) где Р’НСl и Р’Н₂ - фактические парциальные давления хлористого водорода и водорода, выраженные в относительных единицах. Для нахождения относительного давления следует давление, выраженное в паскалях, разделить на стандартное давление, равное Робщ = 101,300 кПа. Определим общее давление, выраженное в относительных единицах: Робщ = Робщ/Рст = 101,3/101,3 = 1. По закону Дальтона парциальное давление компонента газовой смеси равно общему давлению, умноженному на обьемную долю данного компонента: РНСl = Робщ · 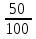 = 0,5; РН₂ = Робщ · = 0,5; РН₂ = Робщ · 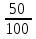 = 0,5. = 0,5.Отсюда произведение фактических парциальных давлений согласно уравнения (24) Пр = (Р’НСl)⁶ /(Р’Н₂)³ = 0,015625/0,125 = 0,125. Сравнивая Kp и Пр, видно, что Kp >Пр (2,36>0,125), т.е. при заданных условиях по уравнению (22) ∆G<0 и возможное направление реакции – слева направо, т.е. в сторону образования Al и HCl. 3.2.3. Определение равновесного состава газовой смеси Для реакций, в которых участвуют только газы или газы и конденсированные фазы, представляющие собой чистые вещества, константу равновесия выражают обычно через равновесные парциальные давления газовых реагентов Рi и обозначают символом Кp. Равновесный состав газовой смеси рассчитывается из выражения константы равновесия рассчитываемой реакции Кр = Р⁶НСl /Р³Н₂ , (25) Где РНСl и РН₂ - равновесные парциальные давления хлористого водорода и водорода, выраженные в относительных единицах. Так как константа равновесия очень велика, Кр = , то очевидно, что реакция при данных фактических концентрациях реагентов потечет вправо. При этом концентрация продуктов реакции будет увеличиваться, а исходных веществ – уменьшаться. Если число молей вещества HCl увеличится на 6х, то число реагента H₂ уменьшиться на 3х. Таким образом, при равновесии количество молей реагентов будут определяться величинами: nН₂ = 0,5 – 3х; nHCl = 0,5 + 6х. При этом их мольные доли составляют: NН₂ = 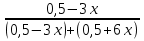 = = 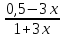 ; ;NHCl = 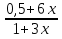 ; ;При этом величины их равновесных парциальных давлений составят: РН₂ = Робщ 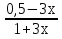 ; РHCl = Робщ ; РHCl = Робщ 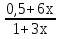 . .Подставив эти значения в уравнение (28), получим Кр = 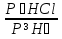 = =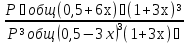 = = 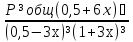 = = Левая часть уравнения представляет собой отношение двух конечных чисел, а правая – очень большое число. Такая ситуация возможна только в случае, если знаменатель стремится к нулю, т.е. либо (0,5-3х)³ →0 или (1+3х)³ →0. Приравнивая последние уравнения к нулю и решая их, получим два корня: х₁ = 0,166666666, х₂ = -0,333. NН₂ = 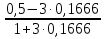 = 0; NHCl = = 0; NHCl = 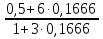 = 0,999=1. = 0,999=1.Таким образом, равновесная газовая фаза будет состоять только из одного реагента НСl, причем их содержание в ней будет Об.%НСl =100%. 3.2.5 Установление направления смещения равновесия Исследуемая реакция идет с поглощением теплоты (∆Н⁰т > 0), следовательно, при повышении температуры равновесие должно смещаться слева направо, так как образование исходных веществ из конечных продуктов является экзотермическим процессом. Увеличение давления смещает равновесие в сторону веществ, занимающих меньший обьем. Увеличение давления смещает равновесие справа налево, в сторону образования водорода. Магнитогорск 2012 |
