Фронтальная лабораторная работа (1). Фронтальная работа
 Скачать 14.53 Kb. Скачать 14.53 Kb.
|
Фронтальная работаОпределение ускорения свободного падения методом математического маятника Частным случаем физического маятника является математический маятник: тело малых размеров (материальная точка), подвешенное на длинной нити, растяжением и весом которой можно пренебречь. Исходя из формулы периода математического маятника математический маятник делает n полных колебаний (численное значение n можно брать произвольно: 10, 20, и т.д.), можно определить ускорение свободного падения g. Если определить период колебания математического маятника длиной l, то можно найти ускорение силы тяжести следующим образом: g 4 2 l T2 Измерения провести 5-10 раз. Найти среднее значение g и вычислить относительную ошибку измерения. 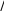  Таблица 1 Таблица 1
КОНТРОЛЬНЫЕ ВОПРОСЫЧто называется измерением? Какие погрешности измерений бывают? Как проводится обработка результатов измерений? Обработка результатов измеренийНайдем среднюю величину ускорения свободного падения и занести в таблицу g g1 g2 g3 g4 g5 5 Найдем абсолютные погрешности для каждого измерения и занесем в таблицу g1 g g1 g2 g g2 g3 g g3 g4 g g4 g5 g g5 Найдем среднее значение абсолютных погрешностей и занесем в таблицу
g 5 Внимание: в числителе все значения стоят по модулю, т.е. знак минус не учитывается! Рассчитаем относительную погрешность наших вычислений и занесем в таблицу (последняя колонка в таблице 1) g100% g 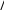 эт Рассчитаем относительную погрешность полученной величины ускорения свободного падения по сравнению с эталонной величиной g 9,8 мс2 .  gэт gэт100% 9,8 g  9,8 9,8100% Ответ запишем в виде g g g мс2 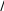 Внимание: Пункты 5 и 6 в таблицу не заносятся. Записываются после ваших вычислений Внимание: Пункты 5 и 6 в таблицу не заносятся. Записываются после ваших вычислений |