дз №1, группа ФН2-101, Голубева. фундаментальные науки
 Скачать 447 Kb.
|
|
Государственное образовательное учреждение высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана» (МГТУ им. Н.Э.Баумана) ________________________________________________________________________ Факультет «ФУНДАМЕНТАЛЬНЫЕ НАУКИ» Кафедра «ПРИКЛАДНАЯ МАТЕМАТИКА»  Домашнее задание по дисциплине « ПРИКЛАДНОЕ ПРОГРАММИРОВАНИЕ В ЗАДАЧАХ МАТЕМАТИЧЕСКОЙ ФИЗИКИ » Домашнее задание №1 5 вариант ИСПОЛНИТЕЛЬ студент гр. ФН2-101 ________________ / Голубева Ю.Ю. / ПРЕПОДАВАТЕЛЬ ________________ / Фисун В. А. / кандидат ф.-м. наук, старший научный сотрудник ИПМ им. М.В.Келдыша РАН. Москва Задание 1. 1.5. Использование математических таблиц для автоматизации арифметических операций. Умножение, деление, возведение в степень и извлечение корня – действия, гораздо более трудоемкие, чем сложение и вычитание, особенно тогда, когда нужно работать с многозначными числами. Настоятельная потребность в таких действиях впервые возникла в XVI веке в связи с развитием дальнего мореплавания, вызвавшим усовершенствование астрономических наблюдений и вычислений. На почве астрономических расчетов и возникли на рубеже XVI и XVII веков логарифмические вычисления, а в настоящее время они применяются повсюду, где приходится иметь дело с многозначными числами. Они выгодны уже при действиях с четырехзначными числами и совершенно необходимы в тех случаях, когда точность должна доходить до пятого знака. Ценность логарифмического метода состоит в том, что он сводит умножение и деление чисел к сложению и вычитанию – действиям менее трудоемким. Возведение в степень, извлечение корня, а также и ряд других вычислений (например тригонометрических) также значительно упрощаются. Открытие логарифмов и логарифмических таблиц Дж. Непером в начале 17 в., позволивших заменять умножение и деление соответственно сложением и вычитанием, явилось крупным шагом в развитии вычислительных систем ручного этапа. Фактически таблицы Непера открыли путь к автоматизации всех арифметических вычислений. В работе "Описание удивительной таблицы логарифмов" (1614) изложил свойства логарифмов, дал описание таблиц, правила пользования ими и примеры применений. Основанием таблицы логарифмов Непера является иррациональное число, к которому неограниченно приближаются числа вида  при безграничном возрастании  . Это число называют неперовым числом и обозначают буквой е:   Впоследствии появился целый ряд модификаций логарифмических таблиц. Однако в практической работе использование логарифмических таблиц имеет ряд неудобств, поэтому Дж. Непер в качестве альтернативного метода предложил специальные счетные палочки (см. рис.), позволявшие производить операции умножения и деления непосредственно над исходными числами. В основу данного метода Непер положил способ умножения решеткой. Наряду с палочками Непер предложил счетную доску для выполнения операций умножения, деления, возведения в квадрат и извлечения квадратного корня в двоичной системе счисления, предвосхитив тем самым преимущества такой системы счисления для автоматизации вычислений. Введенные Дж. Непером логарифмы оказали революционизирующее влияние на все последующее развитие счета, чему в значительной степени способствовало появление целого ряда логарифмических таблиц, вычисленных как самим Непером, так и рядом других известных в то время вычислителей (Х. Бриггс, И. Кепплер, Э. Вингэйт, А. Влах). Сама идея логарифмов в алгебраической интерпретации базируется на сопоставлении двух типов последовательностей: арифметической и геометрической. Логарифмы послужили основой создания замечательного вычислительного инструмента - логарифмической линейки. Прообразом современной логарифмической линейки считается логарифмическая шкала Э. Гюнтера, использованная У. Отредом и Р. Деламейном при создании первых логарифмических линеек. Усилиями целого ряда исследователей логарифмическая линейка постоянно совершенствовалась и видом, наиболее близким к современному, она обязана 19-летнему французскому офицеру А. Манхейму В наши дни при решении ряда задач в информатике, необходимо снизить требуемый объем памяти за счет более медленного выполнения программы или, наоборот, снизить время вычислений за счет увеличения объема используемой памяти. Подход, описывающий это, называется "time-memorytrade-off" («выбор оптимального соотношения "время-память"»). Одним из примеров применения такого подхода являются таблицы поиска. Таблица поиска (англ. lookuptable) – это структура данных, обычно массив или ассоциативный массив, используемая с целью заменить вычисления на операцию простого поиска. Увеличение скорости может быть значительным, так как получить данные из памяти зачастую быстрее, чем выполнение трудоёмких вычислений. Идея такова: вместо того, чтобы, не используя дополнительную память, перебирать все допустимые решения, или один раз вычислить их все заранее и хранить их в памяти (часто нет ни первой, ни второй возможности), можно заранее вычислить часть допустимых значений, и, организовав их в специальную структуру данных — таблицу поиска, — осуществлять с ее помощью дальнейший перебор уже непосредственно при решении задачи. Классический пример использования таблиц поиска — вычисление значений тригонометрических функций, например, синуса. Его непосредственное вычисление может сильно замедлить работу приложения. Чтобы этого избежать, приложение при первом запуске заранее рассчитывает определённое количество значений синуса, например, для всех целых градусов. Потом, когда программе понадобится значение синуса, она использует таблицу поиска, чтобы получить приблизительное значение синуса из памяти, вместо того чтобы вычислять его значение (например, с помощью рядов). Таблицы поиска также используются в математических сопроцессорах; ошибка в таблице поиска в процессорах Pentium фирмы Intel привела к печально известной ошибке, уменьшавшей точность операции деления. Задолго до того, как таблицы поиска появились в программировании, они уже использовались людьми для облегчения ручных вычислений. Особенно были распространены таблицы тригонометрических и статистических функций и логарифмов. Существует промежуточное решение, когда используют таблицу поиска в сочетании с простыми вычислениями — интерполяцией. Это позволяет более точно находить значения между двумя вычисленными заранее точками. Затраты времени немного возрастут, но взамен будет обеспечена бо́льшая точность вычислений. Также эту технику можно применять для уменьшения размеров таблицы поиска без потерь точности. Таблицы поиска широко используются также в компьютерной обработке изображений (в этой области соответствующие таблицы обычно называют «палитрами»). Важно отметить, что использование таблиц поиска в тех задачах, в которых они не эффективны, приводит к ухудшению скорости работы. Это происходит не только потому, что извлечение из памяти данных оказывается медленнее, чем их вычисление, но и потому, что таблица поиска может занять всю память и переполнить кэш. Если таблица велика, каждое обращение к ней, скорее всего, будет приводить к промаху кэша. В некоторых языках программирования (например, в Java) обращение к таблице поиска может быть даже более «дорогим» из-за обязательной проверки границ, включающей в себя дополнительные сравнения и ветвления для каждой операции поиска. Есть два фундаментальных ограничения на создание таблиц поиска. Первое — это общее количество доступной памяти: таблица должна умещаться в имеющийся объём, хотя можно сделать таблицу поиска и на диске, увеличив тем самым время операции поиска. Другое ограничение — это время, необходимое для создания таблицы поиска при первом запуске — хотя обычно эта операция нужна только один раз, она может отнимать слишком много времени, что делает использование таблиц поиска неподходящим решением. Пример. Вычисление синуса. Большинство компьютеров поддерживает только основные арифметические операции и не могут вычислить значение синуса напрямую. Вместо этого для вычисления значения синуса с высокой степенью точности они используют метод CORDIC или ряд Тейлора:  Однако такое вычисление может занять много времени, особенно на медленном процессоре, и существует множество приложений, например, компьютерная графика, которым необходимо вычислять значение тысяч синусов каждую секунду. Распространённое решение — заранее вычислить таблицу значений синуса, и затем нахождение синуса числа сведётся к выбору ближайшего к этому числу аргумента из таблицы (соответствующее значение функции будет близко к правильному значению, потому что синус — непрерывная и ограниченная функция). Например: real array sine_table[-1000..1000] for x from -1000 to 1000 sine_table[x] := sine(pi * x / 1000) function lookup_sine(x) return sine_table[round(1000 * x / pi)] Задание 2. 2.5. Представить программу, добавление в которой отладочного оператора печати влияет на результаты вычислений. В качестве примера для демонстрации возникновения ситуации, в которой добавление в программу отладочного оператора печати влияет на результат вычислений, выберем неустойчивый алгоритм нахождения корня квадратного уравнения   (1)где  (2)Корни уравнения (1) будем определять по формулам:  В качестве начальных данных положим  т.е. решим уравнение  удовлетворяющее условиям (2), наложенным на уравнение (1). Ниже приведен листинг программы, реализованной на языке С++ в кроссплатформенной свободной IDE "QT Creator", осуществляющей поиск корня 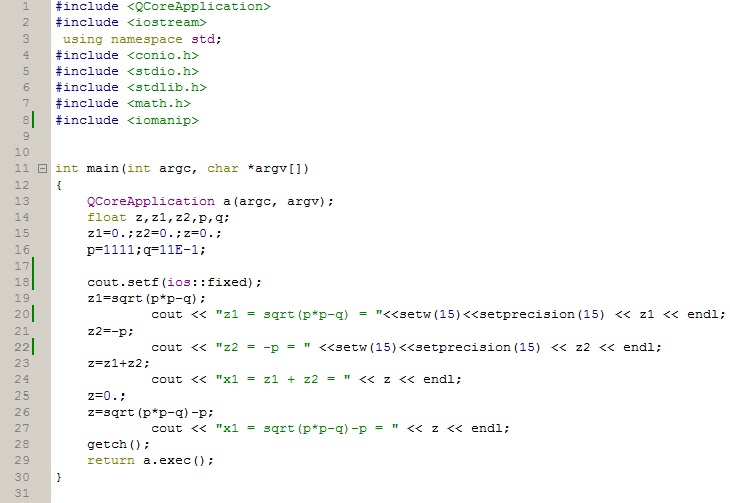 : Результатом работы программы является окно с данными, скриншот которого приведен далее: 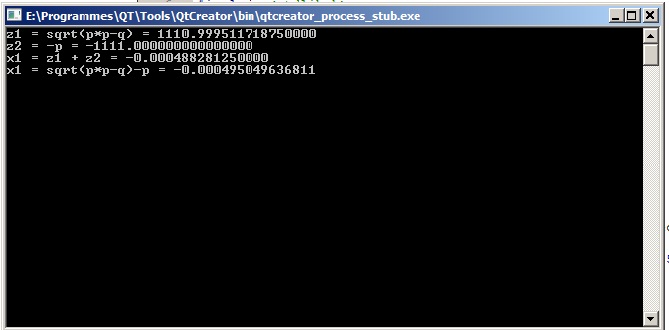 Таким образом, анализируя полученный результат, можно сделать вывод, что значения полученные с добавлением отладочного оператора печати (  ) и без его добавления ( ) различаются уже в 5 знаке после запятой, что может существенно повлиять на вычисления при решении задач, требующих высокой точности.Задание 3. 1.5. Множество вещественных чисел ЭВМ можно представить в виде множества Форсайта  где  - основание системы счисления,  - точность (разрядность мантиссы) и  - интервал значений показателя. Выписать формулу, определяющую значения максимального элемента  Любое число с плавающей запятой можно представить в виде  (3)где  и  Тогда значения максимального элемента множества вещественных чисел, представленные через множество Форсайта, будут определяться формулой:  (4)которая следует из формулы (3) при  и  Формулу (4) можно переписать в виде: 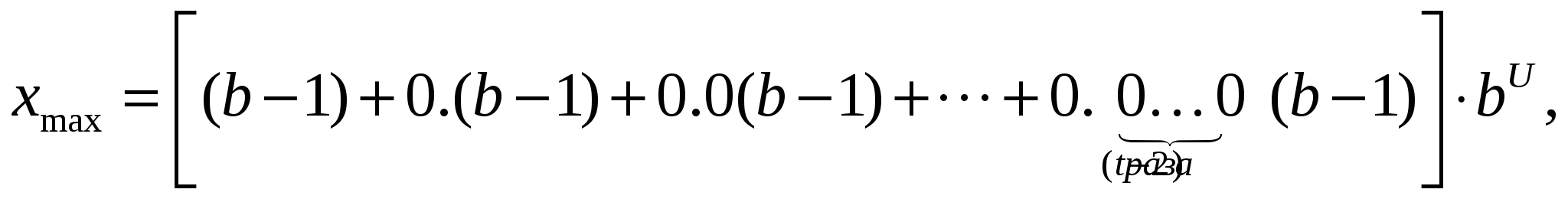 тогда  будем искать в виде суммы  первого члена геометрической прогрессии, для которой знаменатель прогрессии  Таким образом, значения максимального элемента 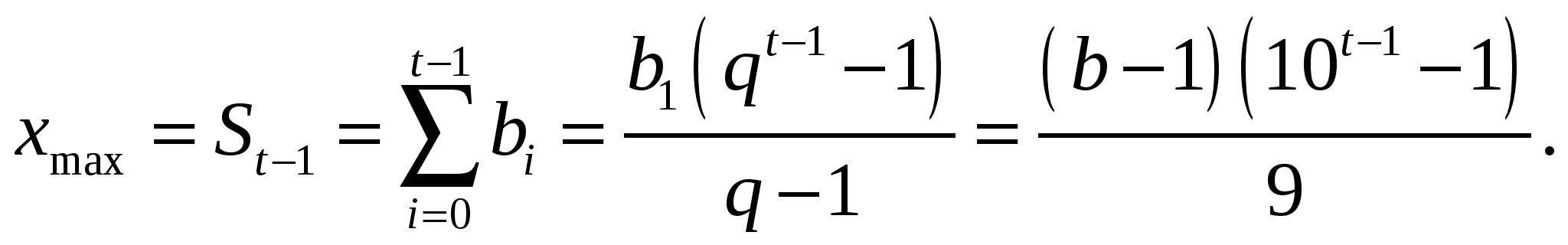 будут определяться по формуле: Задание 4. Перечислить алгоритмы оптимизации в трансляторах с алгоритмических языков, приводящие, иногда, к неоднозначным результатам счета объектных программ. Оптимизирующий компилятор — компилятор, в котором используются различные методы получения более оптимального программного кода при сохранении его функциональных возможностей. Наиболее распространённые цели оптимизации: сокращение времени выполнения программы, повышение производительности, компактификация программного кода, экономия памяти, минимизация энергозатрат, уменьшение количества операций ввода-вывода. Оптимизация может происходить неявно во время трансляции программы, но, как правило, считается отдельным этапом работы компилятора. Компоновщики также могут выполнять часть оптимизаций, таких как удаление неиспользуемых подпрограмм или их переупорядочивание. Среди факторов, влияющих на оптимизацию, отмечаются как вычислительные характеристики целевой машины (например, количество и тактовая частота процессорных ядер, размер процессорного кэша, пропускная способность системной шины, объём оперативной памяти), так и архитектура целевого процессора (в частности, в разных архитектурах доступно различное количество регистров общего назначения, по-разному реализован вычислительный конвейер). Другой класс факторов, влияющих на оптимизацию — сценарии использования целевого программного кода, например, целевые характеристики оптимизации могут значительно отличаться для кода, предназначенного отладки и тестирования, для запуска время от времени, для постоянного использования, для применения во встраиваемых или автономных системах. Среди принципов оптимизации, применяемых в различных методах оптимизации в компиляторах (некоторые из них могут противоречить друг другу или быть неприменимыми при разных целях оптимизации) различают:
Подробнее рассмотрим Visual C++ compiler и примеры алгоритмов оптимизации в трансляторе, приводящие к ошибочным результатам при компиляции. Параметры компилятора /О обеспечивают управление различными способами оптимизации, предназначенными для создания кода максимальной производительности или минимального размера. В следующей таблице описываются параметры /O1 и /O2.
Параметры /O1 и /O2 также включают оптимизацию возврата именованных значений, благодаря чему уменьшается количество вызовов конструкторов копирования и деструкторов временных объектов, хранящихся в стеке. Пример 1. Проблема: Предполагается компилировать файл с исходным кодом C в 64-разрядный двоичный файл с помощью компилятора Visual C/C++ (Cl.exe) в Microsoft Visual Studio 2010. Если включен параметр оптимизации /o1/O1 (минимизировать размер) или параметра оптимизации /o2/O2 (максимизировать скорость), может появиться сообщение об ошибке, подобное приведенному ниже, при попытке компиляции файла: Неустранимая ошибка C1001: Внутренняя ошибка в компиляторе. ("путь и имя файла[0x0000000054BA3E3C:0x0000000000000044]", созданного компилятором файла строки номер строки) Примечания: Эта проблема возникает только при компиляции файла из исходного кода на 64-разрядный двоичный файл с / O1 или/O2 оптимизации параметр включен. Эта проблема не возникает при отключении обоих параметров оптимизации или при компиляции файла исходного кода для 32-разрядных двоичных файлов. Пример 2. Проблема: Операторы побитового сдвига возвращают неверные результаты при запуске приложения, скомпилированного с помощью Visual C++ 2010 компилятор x86 с параметром /o2/O2 (максимизирование скорости) или оптимизацией /Ox (полная оптимизация). Эту проблему демонстрирует следующий код: #include #include int main(int argc, char ** argv) { short lActualOutput; const char * mBytes; char x[5]; char lBuffer[2]; for (int i = 0; i < 5; i++) { x[i] = 97+i; } mBytes=&x[3]; size_t aSize = sizeof(lBuffer); memcpy(lBuffer, mBytes, aSize); mBytes += aSize; lActualOutput = (lBuffer[0] << 8) + lBuffer[1]; fprintf(stdout, "lActualOutput= 0x%04X \n", lActualOutput); } Получается неправильный следующий результат: lActualOutput = 0x6464 Ожидаемый результат выглядит следующим образом: lActualOutput = 0x6465
Пример 3. Проблема: Неправильный код компьютера создается для оператора «switch» в x64 компилятора Visual C++ 2010 при включении компилятора /Ob1(Only_inline), /o1/O1 (минимизировать размер), /o2/O2 (максимизировать скорость), /Ox(полная оптимизация) или параметра оптимизации компилятора /Og (виды глобальной оптимизации). Эту проблему демонстрирует следующий код: #include int test(int bps, int sflags) { if (sflags & (1 << bps)) { switch (bps) { case 1: return 1; case 2: return 3; default: return 0; } } else { switch (bps) { case 1: return 2; default: return 0; } } } void main() { int res = test(1, -1); printf("%d\n", res); } Ожидаемый результат: 1. Фактический результат равен 0. | |||||||||||||