К.р. №8 в. 6 Функции комплексной переменной и операционное исчисление. К.р. №8 в. 6 Функции комплексной переменной и операционное исчис. Функции комплексной переменной и операционное исчисление
 Скачать 260 Kb. Скачать 260 Kb.
|
|
Высшая математика. Контрольная работа №8. Тема: Функции комплексной переменной и операционное исчисление. 366.Представить заданную функцию w=f(z), где z=x+iy, в виде w=u(x,y)+iv(x,y); проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке z0: Решение. Так как 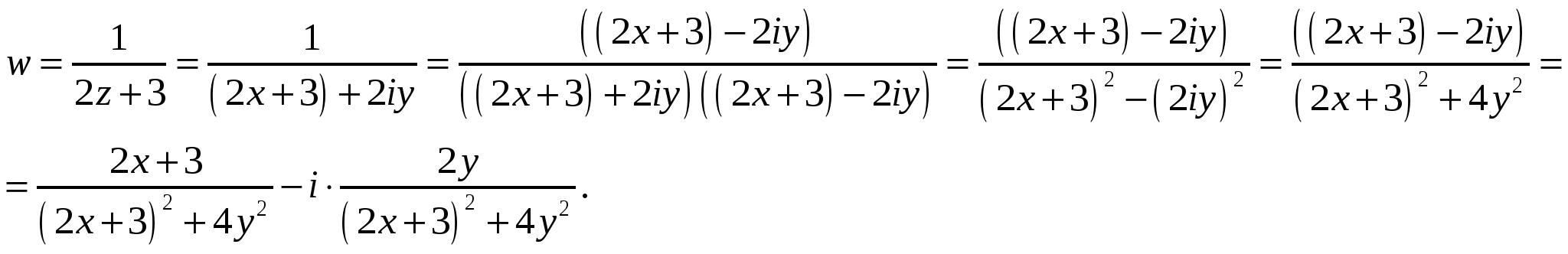 Тогда 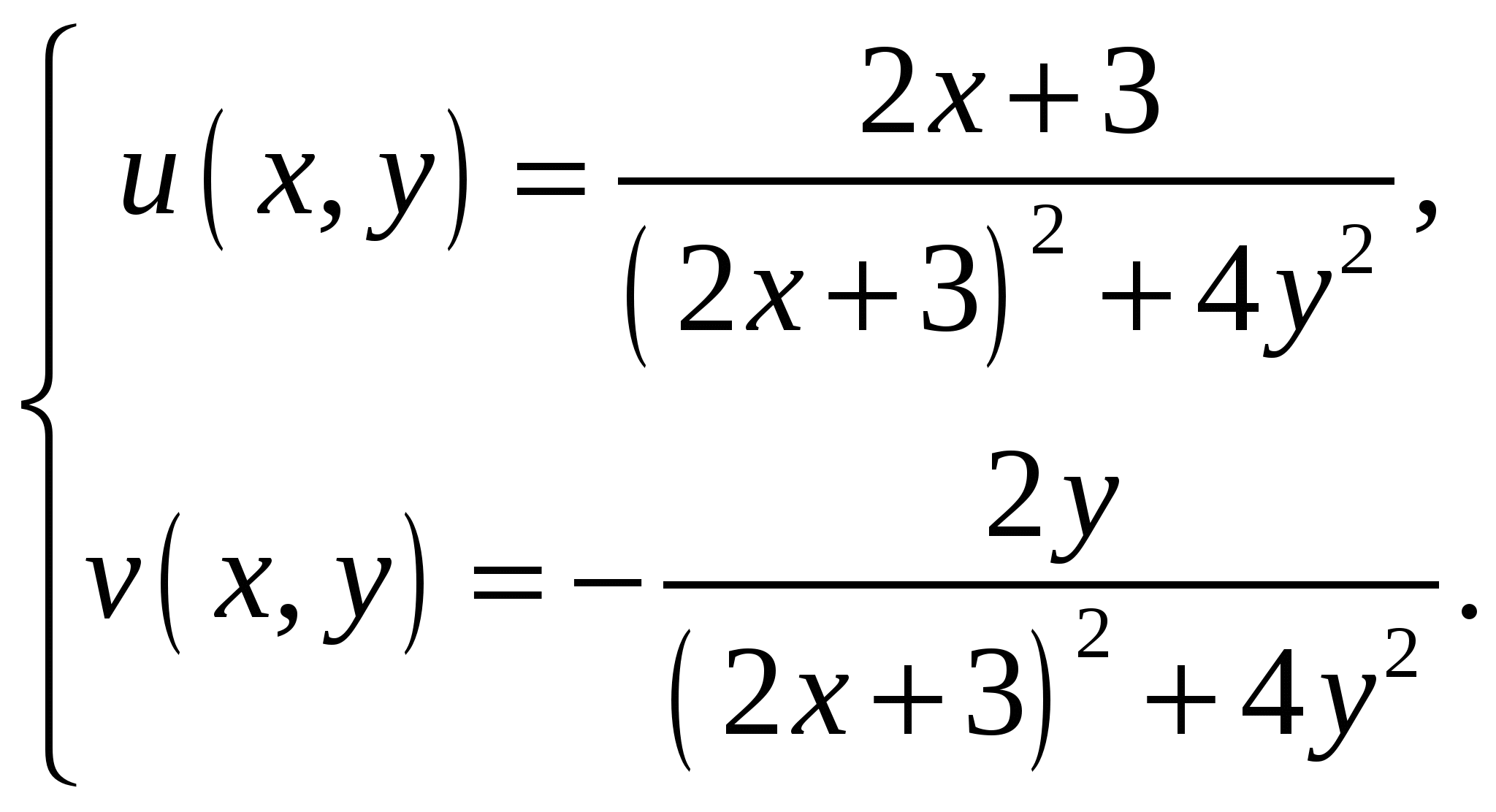 Функция является аналитической, то выполняются условия Коши – Римана 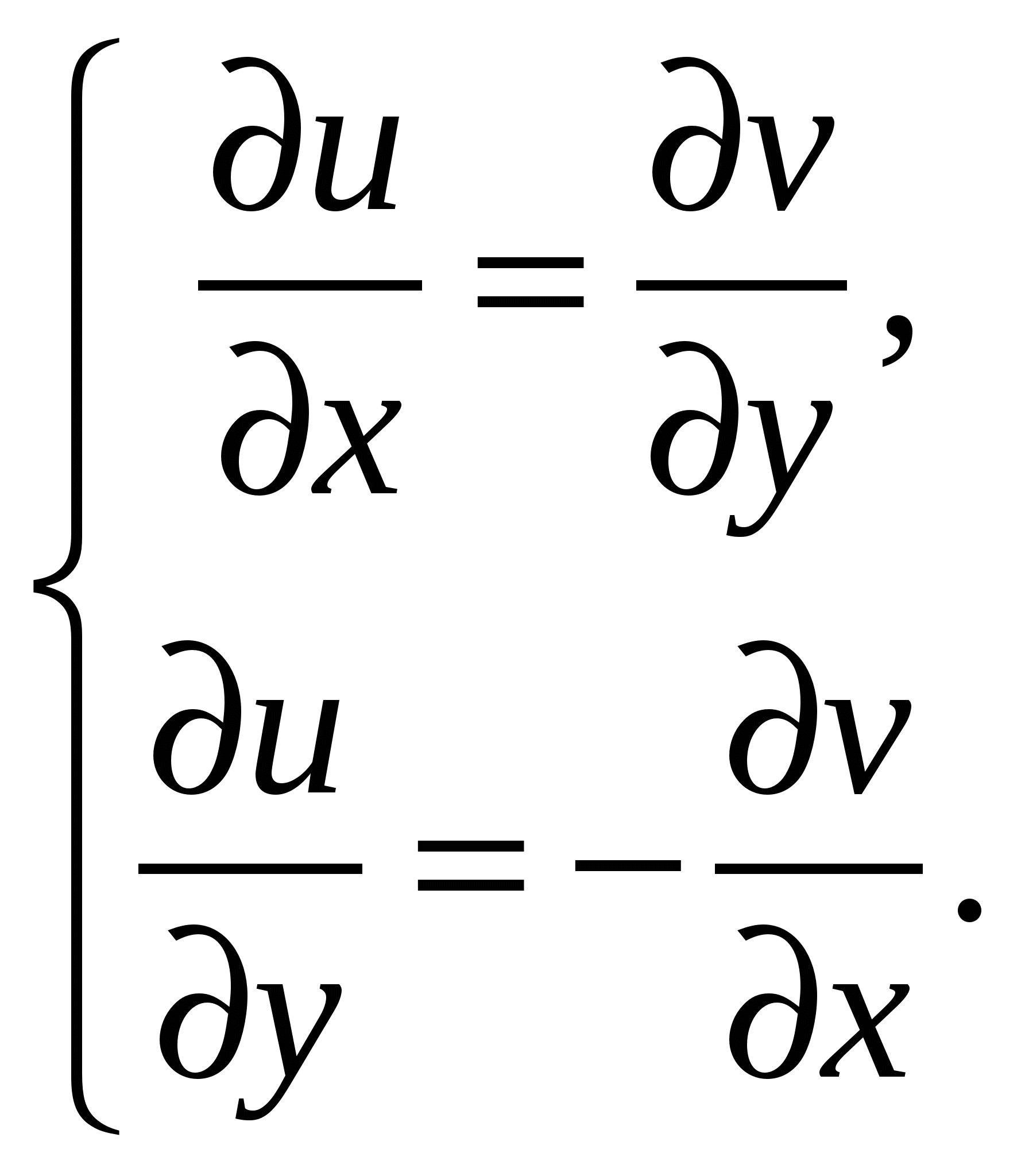 Вычислим частные производные, 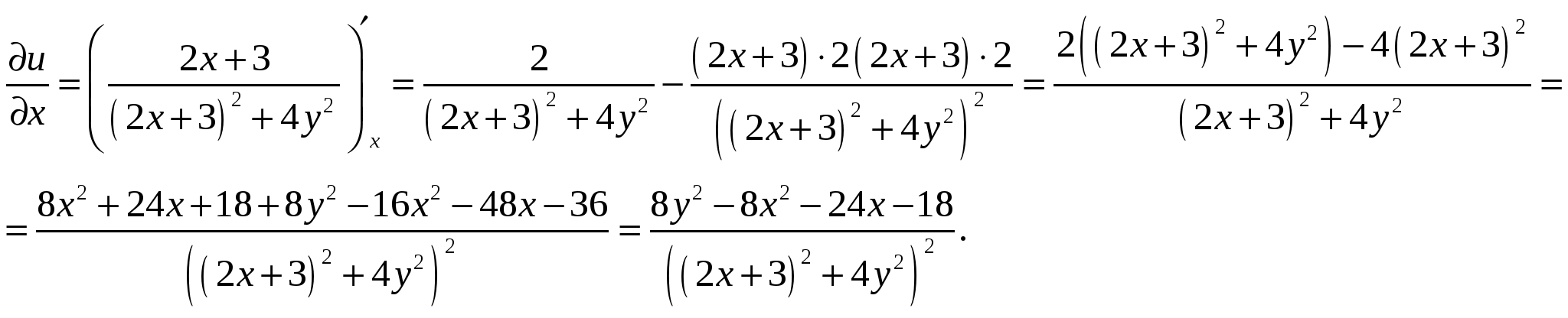 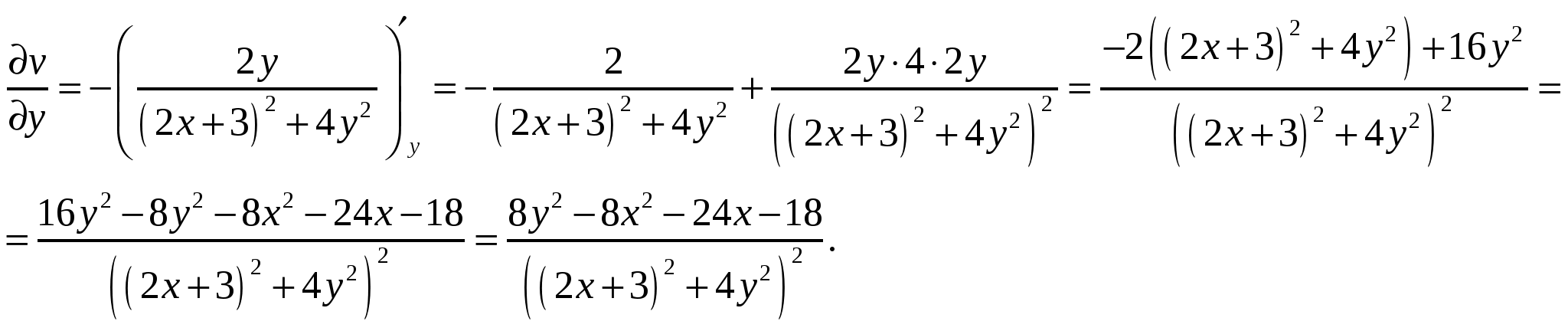 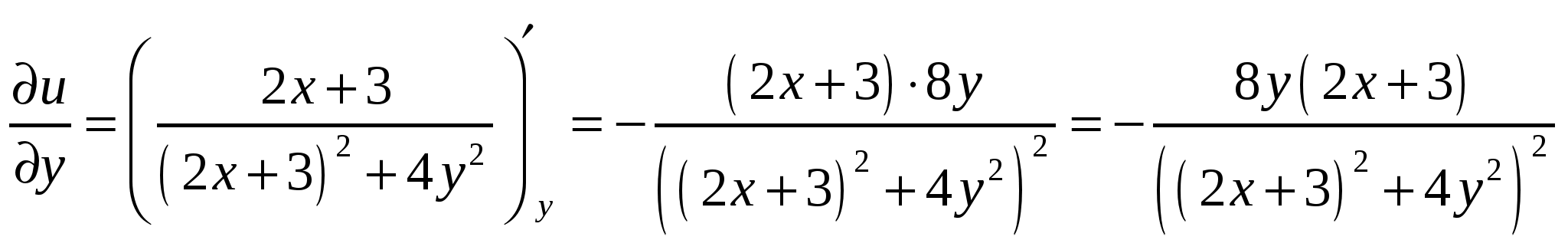 , ,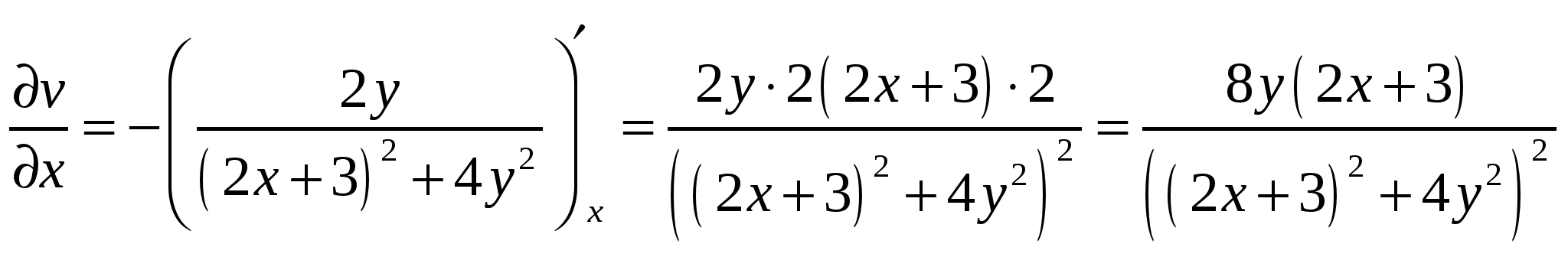 . .Получим Вычислим производную в точке 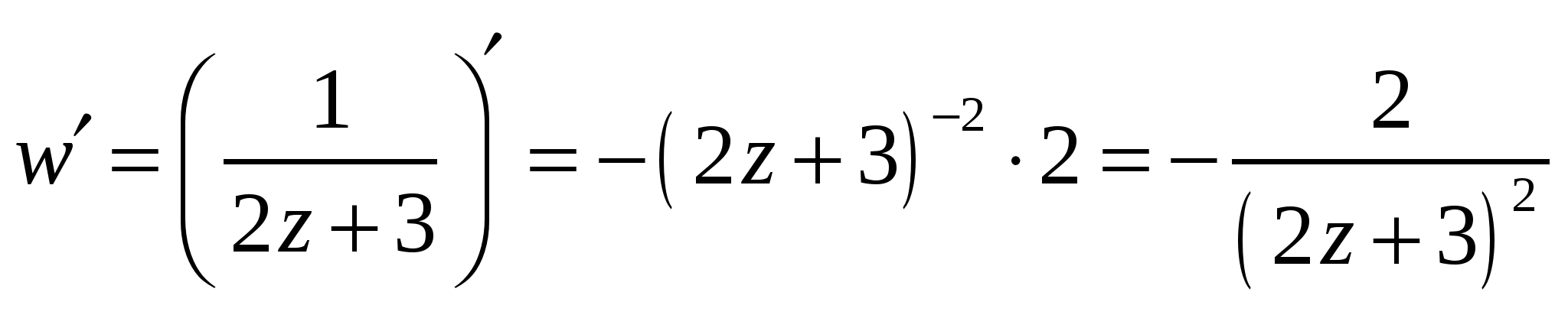 , тогда , тогда 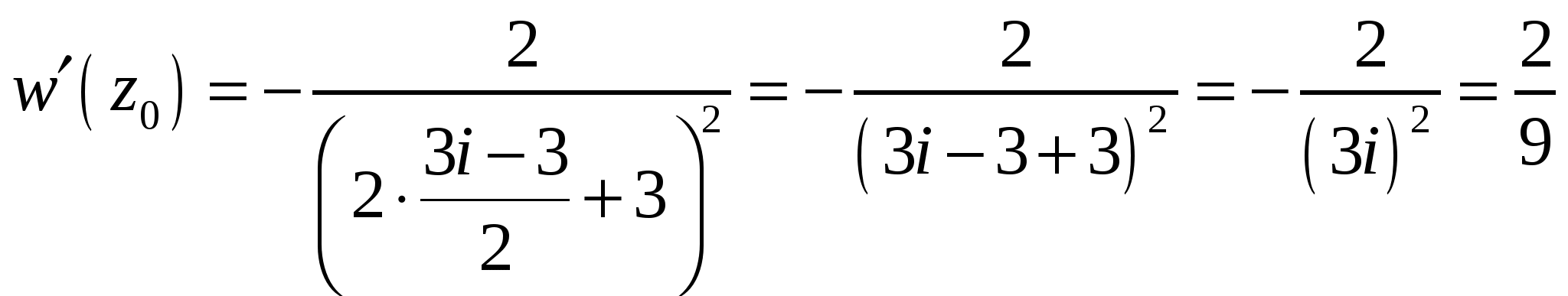 . .376.Разложить функцию f(z) в ряд Лорана в окрестности точки z0: Решение. Представим функцию в виде Далее используем разложение в ряд функций 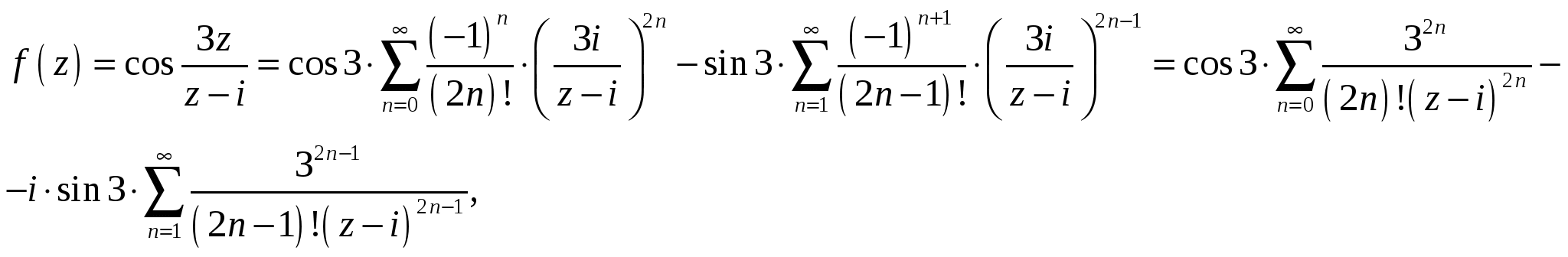 386.Определить область (круг) сходимости данного ряда и исследовать сходимость его (расходится, сходится условно, сходится абсолютно) в точках z1, z2, z3: Решение. Для данного степенного ряда 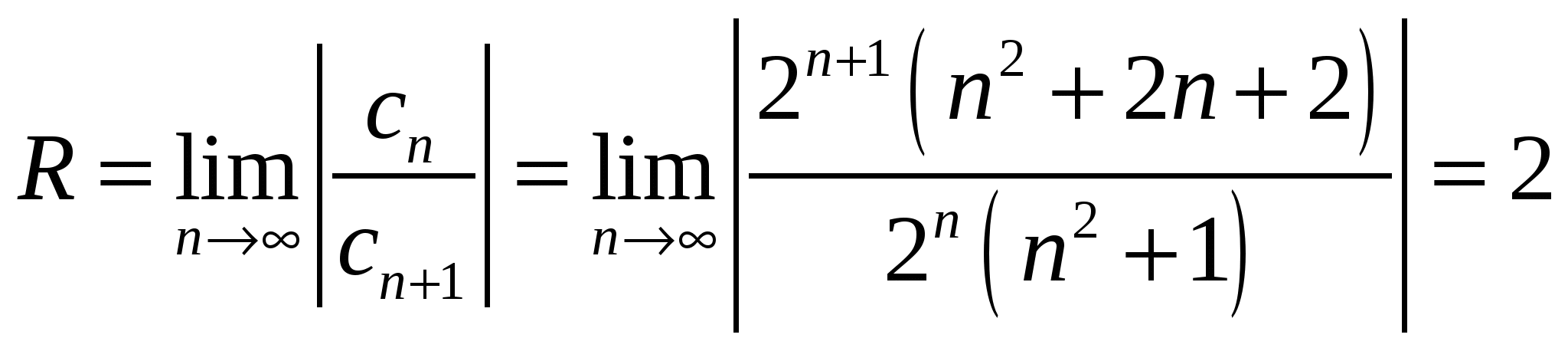 . .Область сходимости ряда определяется неравенством Точка Точка Точка 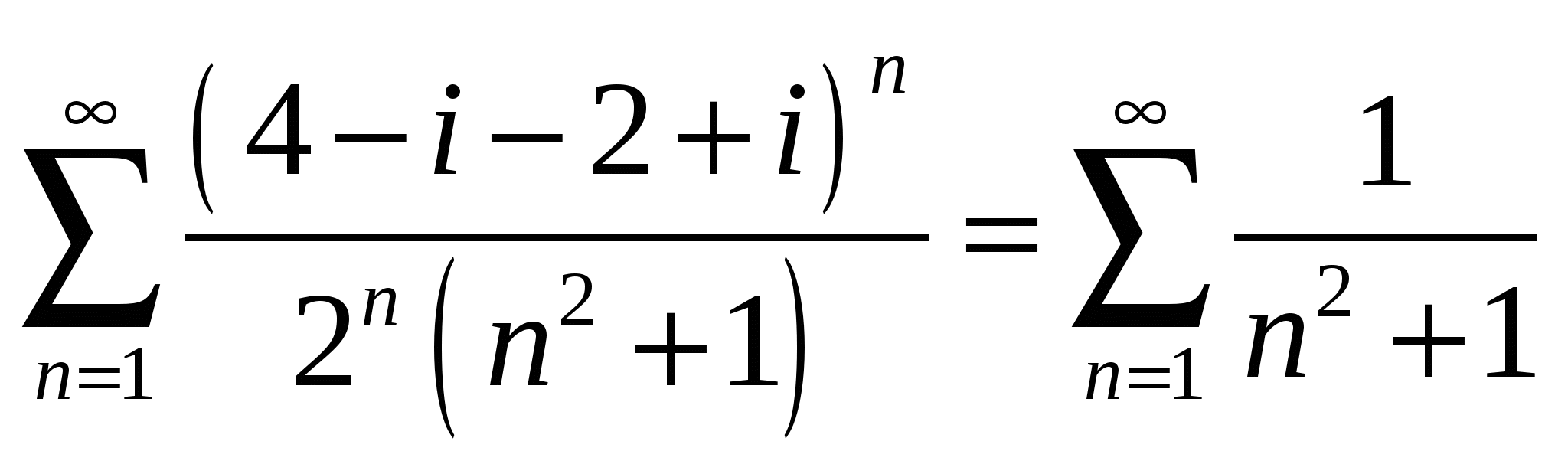 . .Сравним данный ряд с рядом 396.При помощи вычетов вычислить данный интеграл по контуру l: 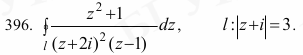 Решение. Функция 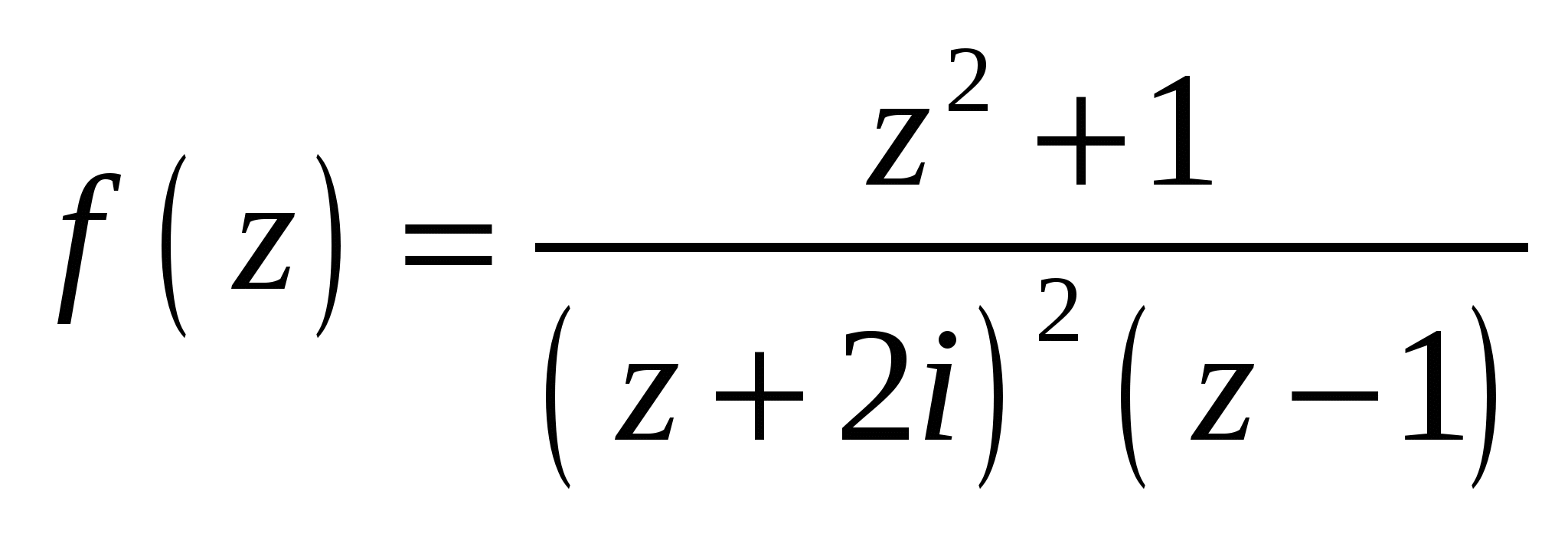 внутри контура интегрирования имеет особые точки: внутри контура интегрирования имеет особые точки: 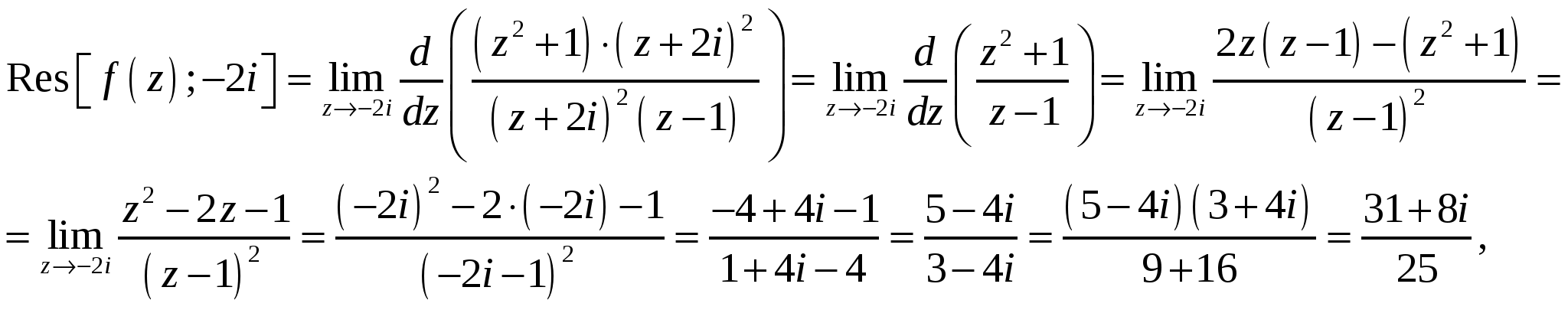 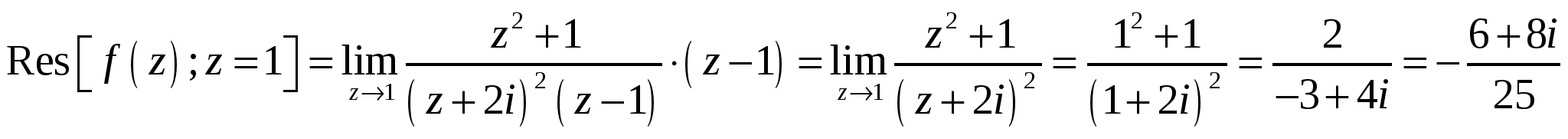 . .Тогда интеграл равен 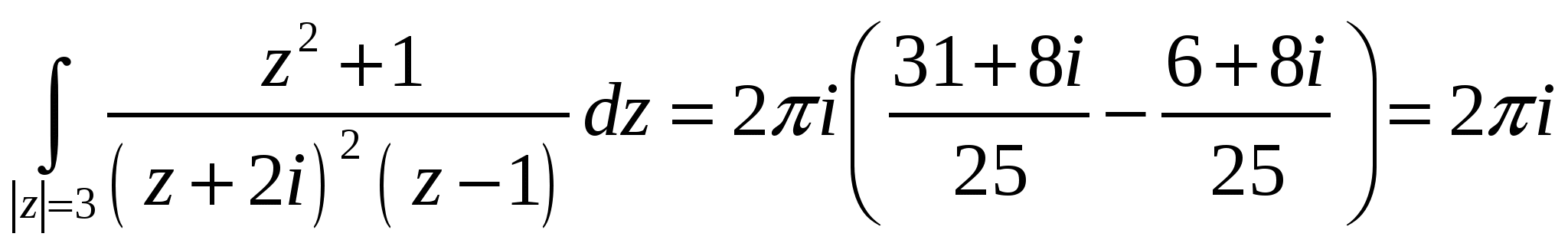 . .Ответ: 406.Найти изображение заданного оригинала f(t): Решение. По таблице основные оригиналы и их изображения 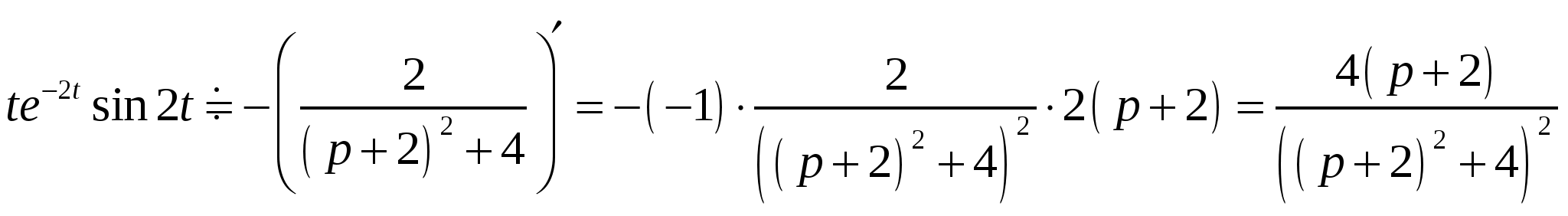 . .Ответ: 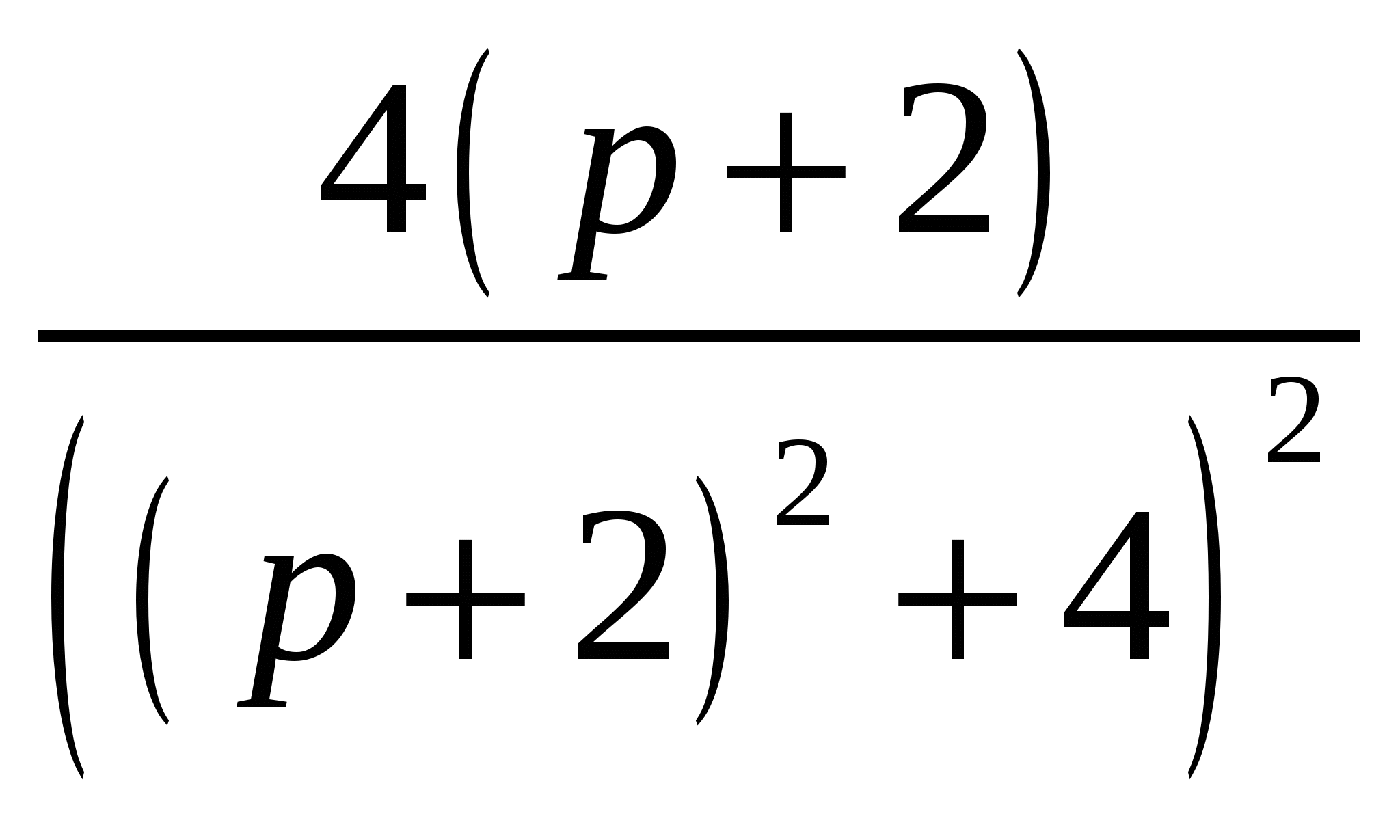 . .416. Найти изображение заданного оригинала f(t): Решение. По таблице оригиналов и используя свойство линейности 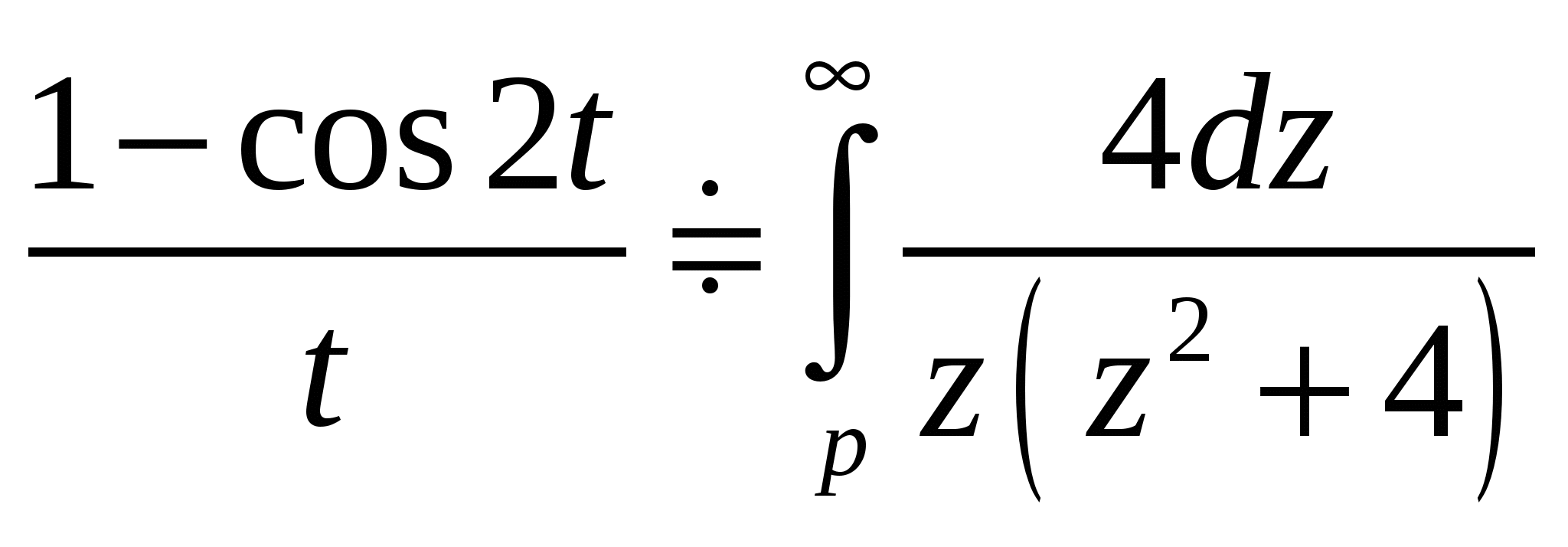 . Пычислим несобственный интеграл. Для этого дробь . Пычислим несобственный интеграл. Для этого дробь Тогда 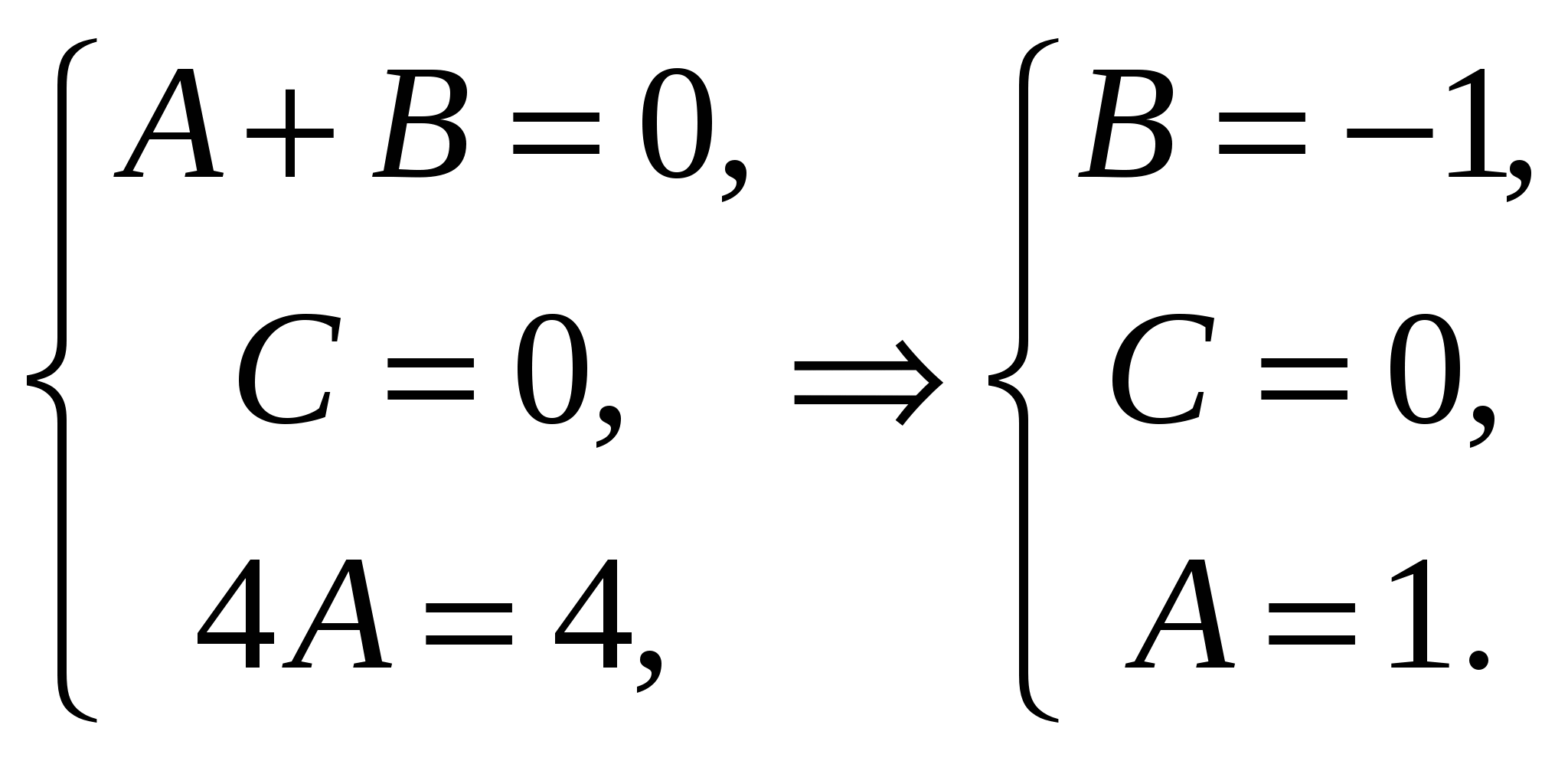 Получим 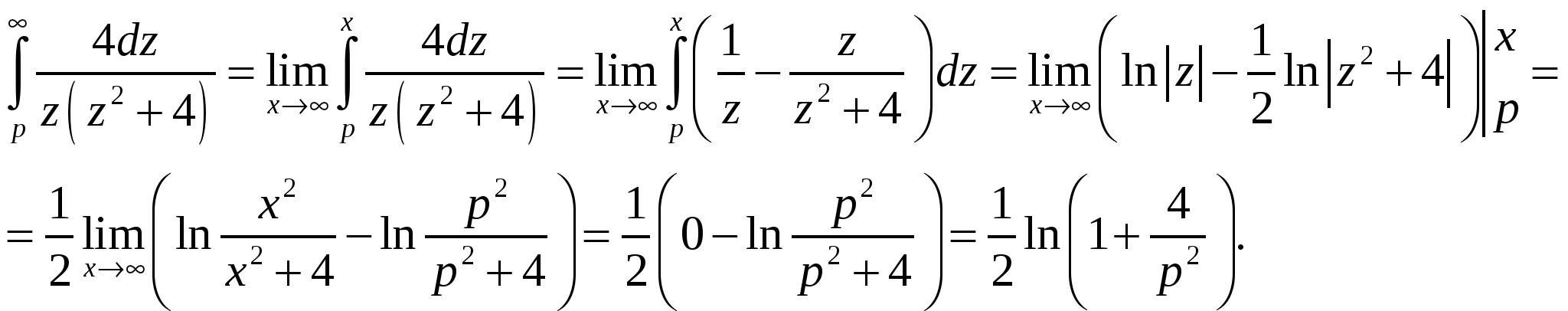 По теореме интегрирования оригинала 426.Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям: Решение. Пусть 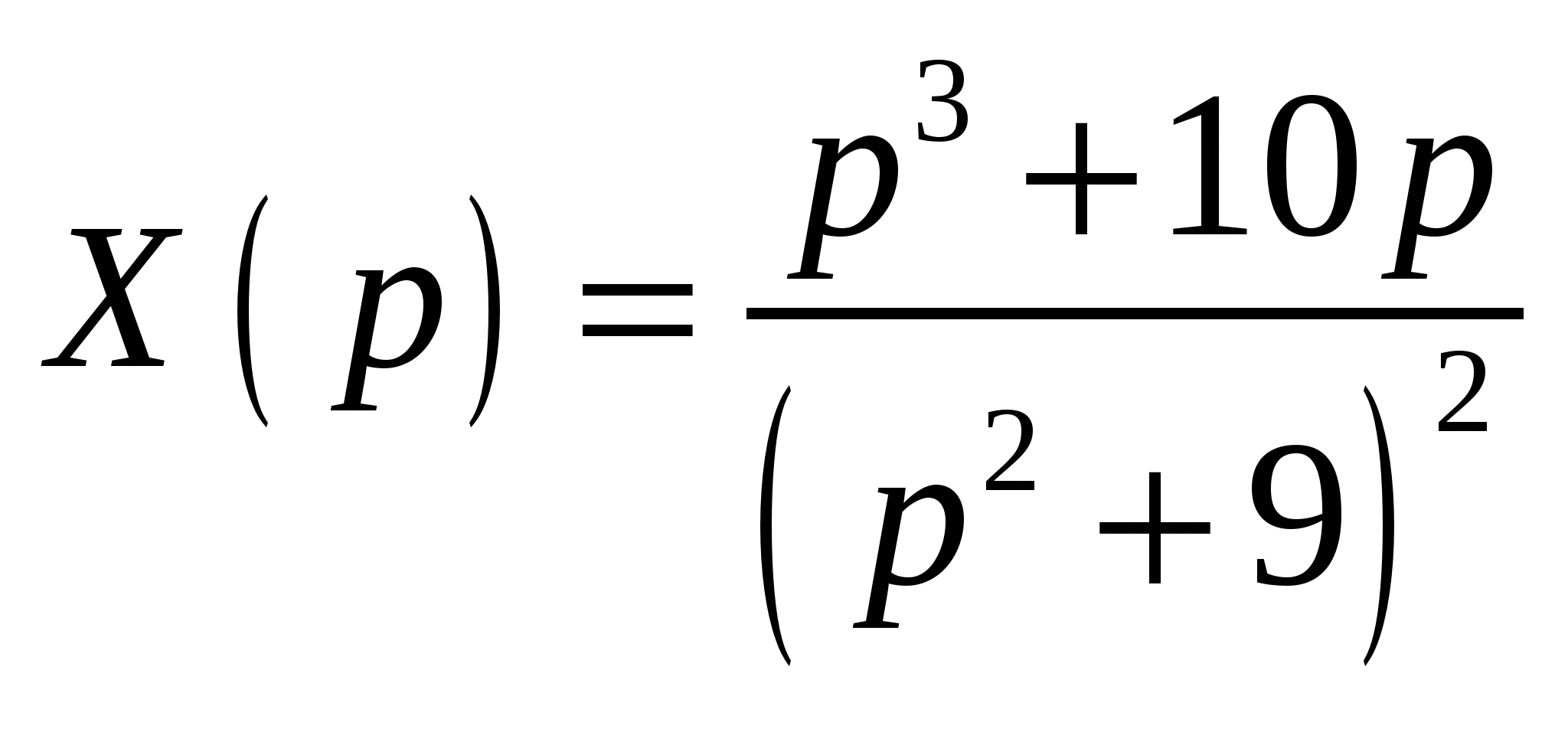 . .Представим дробь 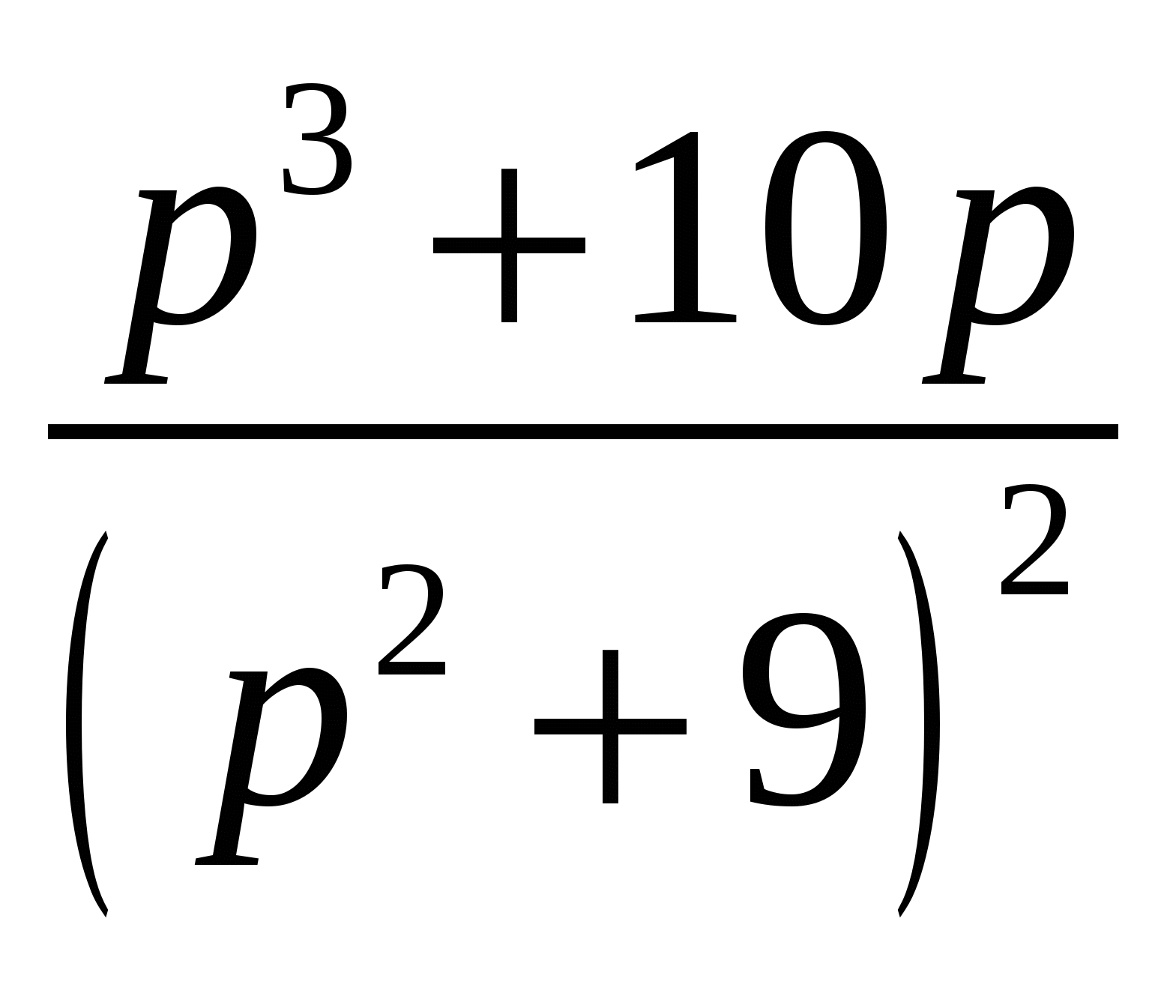 в виде суммы простых дробей, т.е. в виде суммы простых дробей, т.е. 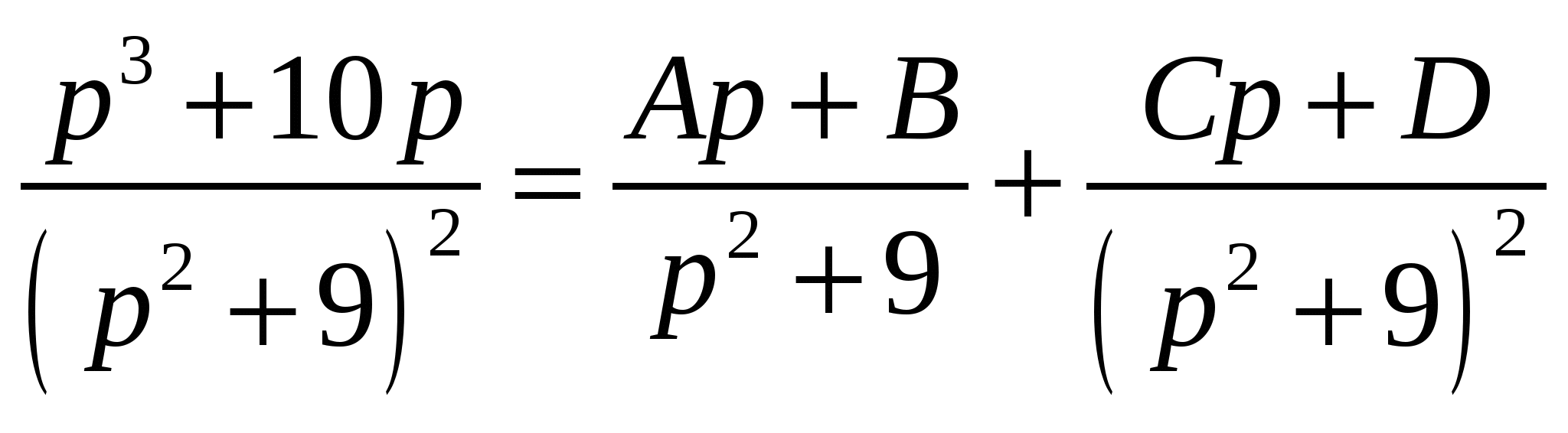 . Найдем коэффициенты . Найдем коэффициенты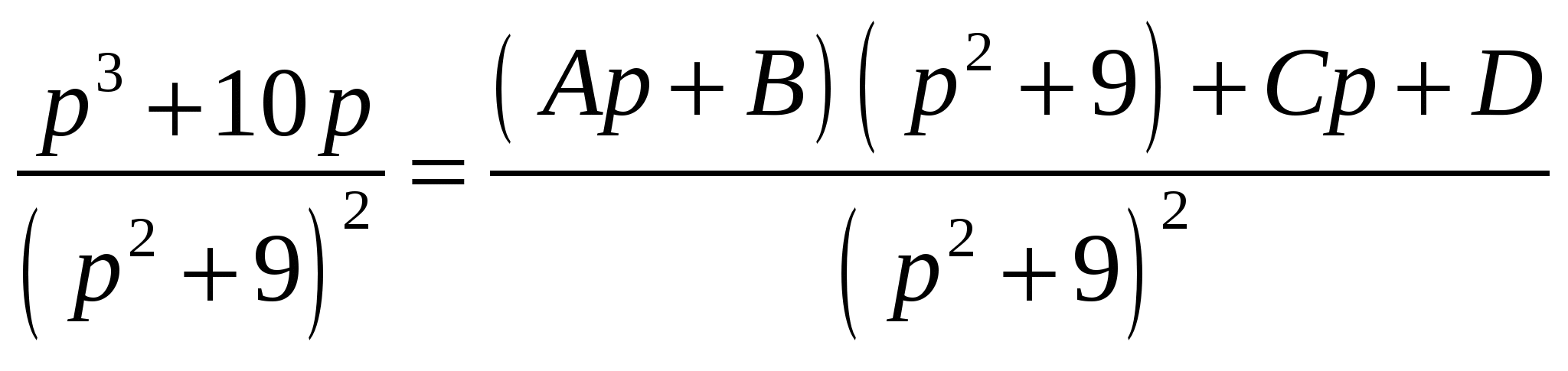 , ,Тогда 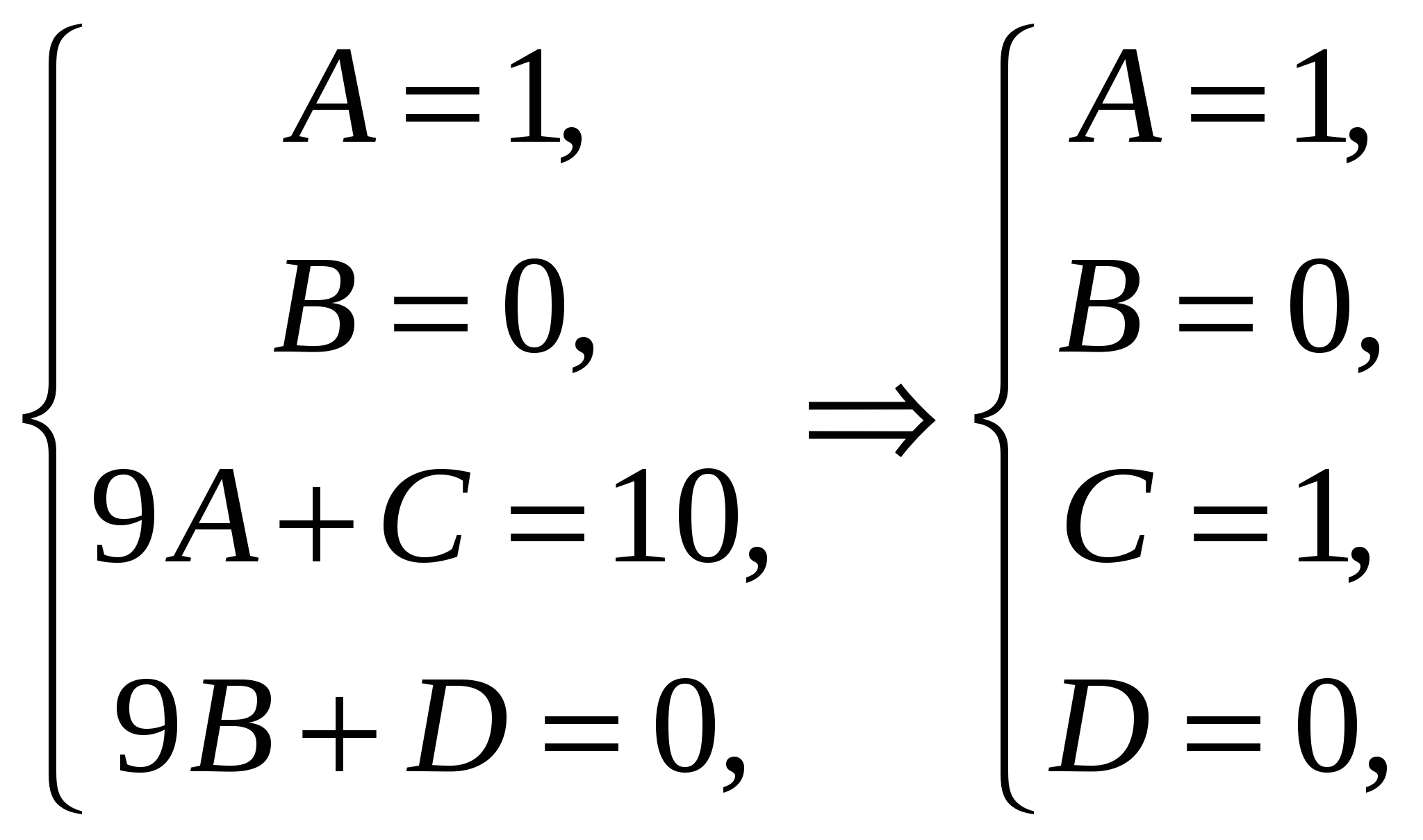 Получим 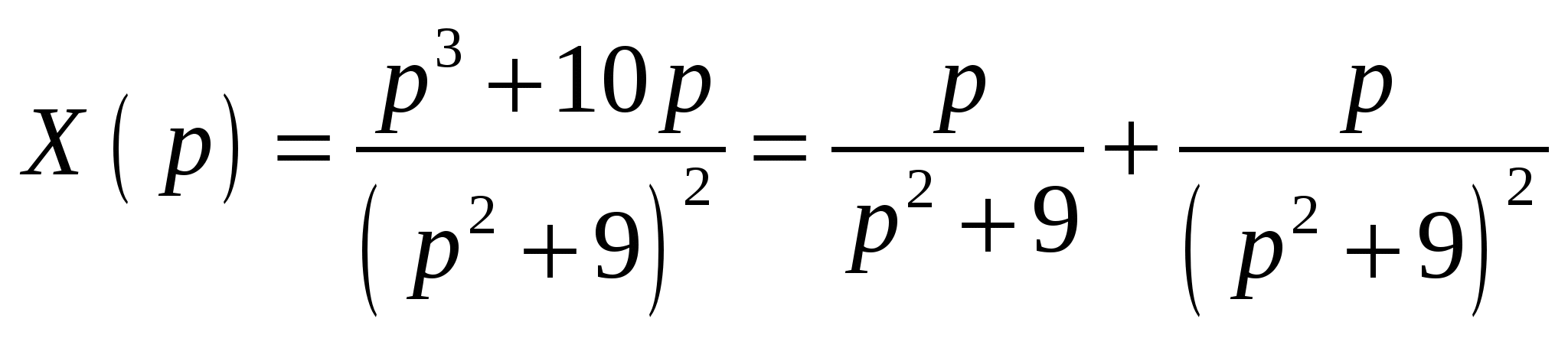 . .Переходя к оригиналам, получаем Ответ: |
