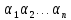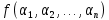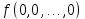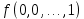функции. Функции многозначной логики. Функции многозначной логики
 Скачать 44.11 Kb. Скачать 44.11 Kb.
|
|
Функции многозначной логики Обозначим Ek= {0,1,2,...,k-1}, k > 2. Пусть 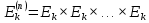 (n раз). Рассмотрим отображение (n раз). Рассмотрим отображение 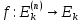 , где аргумент , где аргумент 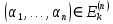 . .Определение. Функцией k-значной логики называется функция произвольного фиксированного числа переменных, у которой как переменные, так и сама функция принимают значения из 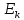 . .Таким образом, функция k-значной логики 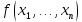 отображает отображает 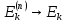 . Функцию . Функцию 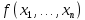 , как и булеву функцию, можно задать в виде таблицы: , как и булеву функцию, можно задать в виде таблицы:
Обозначим через множество всех k-значных функций (или 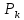 – k-значная логика), через – k-значная логика), через 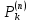 – множество всех функций из – множество всех функций из 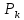 , зависящих от n переменных. , зависящих от n переменных.Утверждение 1. | 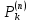 |= |=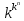 (очевидно из табличного задания). (очевидно из табличного задания).Понятия существенных и фиктивных переменных, понятие равенства функций, формула и реализация функций формулами, эквивалентность формул – всё как в 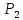 . .Рассмотрим важнейшие функции k-значной логики: 1. Константы 0, 1, 2,..., k-1 2. x+1 (по модулю k) 3. N(x)=k–1–x (отрицание Лукашевича) 4. 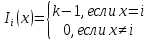 5. 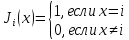 6. Максимум , т.е. 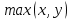 7. 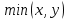 8. 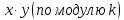 9. 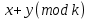 Замечание. Функции 6. – 9. коммутативны и ассоциативны. 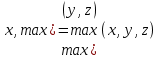 , , 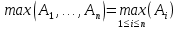 . .Утверждение 2. Для любой функции 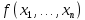 из из 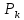 имеет место представление: имеет место представление: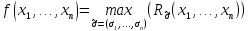 , где , где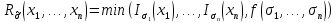 . .Доказательство. Пусть 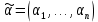 . Рассмотрим . Рассмотрим 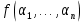 . Надо показать, что слева и справа стоят одинаковые значения. Вычислим . Надо показать, что слева и справа стоят одинаковые значения. Вычислим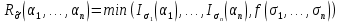 . .1-й случай. 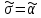 , тогда , тогда 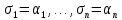 . Поэтому . Поэтому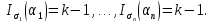 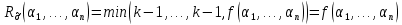 . .2-й случай. 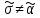 . Тогда существует i-й разряд такой, что . Тогда существует i-й разряд такой, что 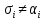 , поэтому , поэтому 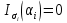 . Следовательно, . Следовательно, 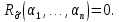 В итоге получаем max(0,...,0, 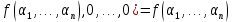 . ЧТД . ЧТДОпределение. Система функций называется полной, если её замыкание совпадает с 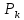 . .Следствие 1. Система {0,1,...,k-1,I0(x),...,Ik-1(x), max(x,y), min(x,y)} полна в 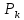 . .Утверждение 3. Система {0,1,...,k-1,I0(x),...,Ik-1(x), max(x,y), x+1} полна в 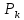 . .Утверждение 4. Система {max(x,y), x+1} полна в 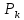 . .Определение. Функция Вебба Vk(x,y)=max(x,y)+1. Утверждение 5. Система {Vk(x,y)} полна в 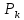 . .Доказательство. 1) Подставим вместо x,y просто x, тогда Vk(x,x)=max(x,x)+1=x+1. 2) Vk(x,y)+1+1...+1 (k-1 раз) = max(x,y)+1+...+1 (k раз)=max(x,y).ЧТД Теорема 1. Существует алгоритм для распознавания полноты конечных систем функций в 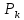 . .Замечание. Число предполных классов в 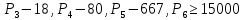 . .Теорема 2. Система полиномов полна в 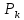 , если и только если k –простое. , если и только если k –простое.Теорема 3. Для любого 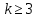 в в 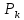 существует замкнутый класс, не имеющий базиса. существует замкнутый класс, не имеющий базиса.Замечание. Понятие базиса в 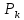 совпадает с соответствующим понятием в совпадает с соответствующим понятием в 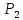 . .Теорема 4. Для любого 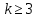 в в 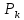 существует замкнутый класс со счётным базисом. существует замкнутый класс со счётным базисом.Теорема 5. Для любого 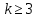 в в 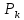 существует континуум замкнутых классов. существует континуум замкнутых классов.ОТЛИЧИЯ 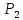 от от 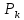 1) В 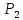 существует счётное множество замкнутых классов. существует счётное множество замкнутых классов.2) В 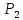 каждый замкнутый класс имеет конечный базис. каждый замкнутый класс имеет конечный базис.3) В 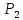 каждая функция представима единственным образом в виде полинома по mod 2. каждая функция представима единственным образом в виде полинома по mod 2.А как в 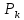 ? ?1) В 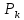 существует континуум замкнутых классов. существует континуум замкнутых классов.2) В 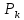 существует замкнутый класс, не имеющий базиса. существует замкнутый класс, не имеющий базиса.3) В 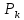 существует замкнутый класс, который имеет счётный базис. существует замкнутый класс, который имеет счётный базис.4) Система полиномов полна в 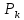 iff k – простое число. iff k – простое число. |