Задача. Изменить порядок интегрирования. Изменить порядок интегрирования. Функция двух переменных
 Скачать 174.87 Kb.
|
|
Теория. Двойной интеграл в общем виде записывается следующим образом:  Разбираемся в терминах и обозначениях:  – значок двойного интеграла;D – область интегрирования (плоская фигура); f(x,y) – подынтегральная функция двух переменных, часто она довольно простая; dx, dy – значки дифференциалов. Что значит вычислить двойной интеграл? Вычислить двойной интеграл – это значит найти ЧИСЛО.  , где С=constРезультат (число С) может быть отрицательным. Как вычислить двойной интеграл? Для того чтобы вычислить двойной интеграл, его необходимо свести к повторным интегралам. Сделать это можно двумя способами. Наиболее распространён следующий способ: 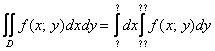 Вместо знаков вопроса необходимо расставить пределы интегрирования. Причём одиночные знаки вопроса ? у внешнего интеграла – это числа, а двойные знаки вопроса ?? у внутреннего интеграла – это функции одной переменной y=f(x) , зависящие от «икс». Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область D. Область D представляет собой обычную плоскую фигуру. После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл 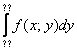 , а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.Грубо говоря, задача сводится к вычислению двух определённых интегралов. Второй способ перехода к повторным интегралам встречается несколько реже:  Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками – будут другими! Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции x=g(y), зависящие от «игрек». Какой бы мы ни выбрали способ перехода к повторным интегралам, окончательный ответ обязательно получится один и тот же:  Формулы для вычисления двойного интеграла созданы для двух стандартных областей: областей 1-го и 2-го типов. Они изображены на рис.1.  Формула Вычисления двойного интеграла для области 1-го типа: 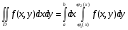 Формула вычисления двойного интеграла для области 2-го типа:  Задача. Изменить порядок интегрирования  Решение: Область интегрирования задается следующими условиями:  Изобразим область интегрирования на чертеже (выделено серым цветом):  Задача состоит в том, чтобы просканировать лучом «лазера» (красным вдоль оси OX, оранжевым – вдоль оси ОY) каждую точку закрашенной области 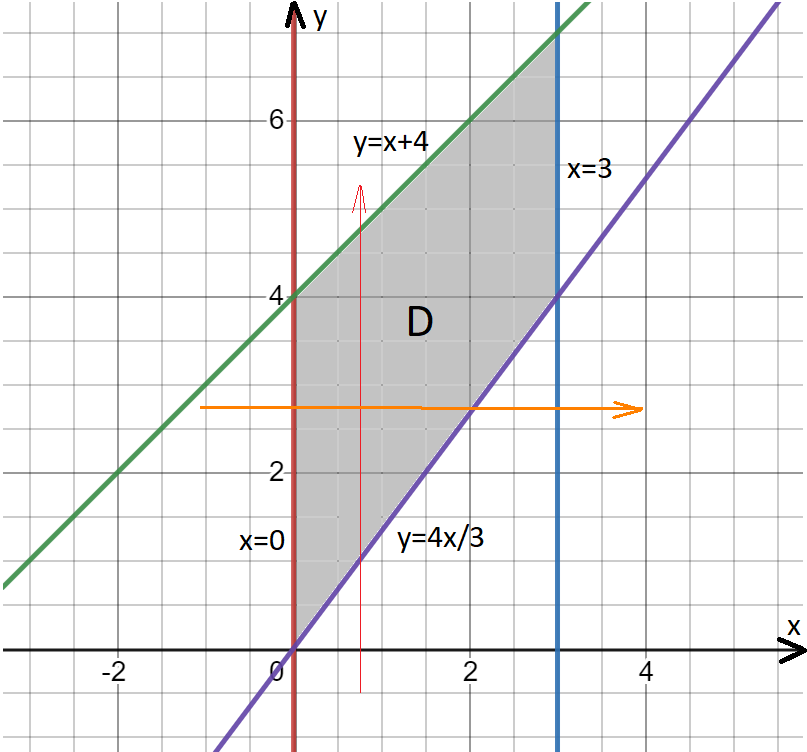 Красный луч лазера проходит область интегрирования строго снизу вверх, то есть указку вы ВСЕГДА держите ниже плоской фигуры. Луч входит в область через прямую, которая задаётся уравнением у=4x/3 и выходит из области через прямую у=x+4. Чтобы просветить всю область, вам нужно строго слева направо провести указкой вдоль оси OX от 0 до 3. Итак, что получилось: «игрек» изменяется от 4x/3 до x+4; «икс» изменяется от 0 до 3. В задачах вышесказанное записывают в виде неравенств:  Данные неравенства называют порядком обхода области интегрирования или просто порядком интегрирования Это и задает исходный двойной интеграл, в котором необходимо поменять порядок интегрирования. Теперь необходимо перейти к повторному интегралу вторым способом. Смотрим на функции, которыми задается область 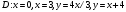 . Если совсем просто, то перейти к обратным функциям, это значит – выразить «иксы» через «игреки».Если y=4x/3, то x=3y/4 Если y=x+4, то x=y-4 Обходим область интегрирования вторым способом (по оранжевой указке): Теперь лазерную указку держим слева от области интегрирования. Луч лазера проходит область строго слева направо. Чтобы просканировать лазером всю область, нужно провести указкой вдоль оси OY строго снизу вверх от 0 до 8. В данном случае луч входит в область через разные прямые и выходит из области через разные прямые. В таких случаях следует разделить область интегрирования на две части и для каждой из частей составить свои повторные интегралы:  1) Если «игрек» изменяется от 0 до 4, то луч входит в область через x=0 и выходит через прямую x=3y/4. Поэтому порядок обхода области будет следующим:  И соответствующие повторные интегралы:  2) Если «игрек» изменяется от 4 до 8, то луч входит в область через прямую x=y-4 и выходит через прямую x=3. Следовательно, порядок обхода области будет следующим:  И соответствующие повторные интегралы: 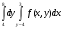 У определенных и кратных интегралов есть свойство аддитивности, то есть, их можно сложить, что в данном случае и следует сделать:  – это и есть искомый обход области вторым способом в виде суммы двух интегралов.Ответ записываем так:  |