18. Понятие двойного интеграла. Основные определения. Свойства. Замена переменных в двойном интеграле. Приложения двойного интеграла
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
18. Понятие двойного интеграла. Основные определения. Свойства. Замена переменных в двойном интеграле. Приложения двойного интеграла. Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл, а на случай функций трех переменных – тройной интеграл. Пусть в замкнутой области D плоскости Oxy задана непрерывная функция z = f (x, y) . Разобьем область D на n элементарных областей Di (i = ,1 n ), площади которых обозначим через 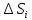 , а диаметры (наибольшее расстояние между точками области) – через di. В каждой области Di выберем произвольную точку , а диаметры (наибольшее расстояние между точками области) – через di. В каждой области Di выберем произвольную точку 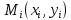 , после чего составим сумму , после чего составим сумму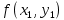 ∆ ∆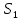 + + 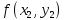 ∆ ∆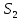 +…+ +…+ 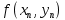 ∆ ∆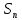 = =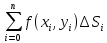 которая называется интегральной суммой для функции f (x, y) в области D. Обозначим через d наибольший из диаметров областей Di . Тогда стремление d к нулю будет означать измельчение разбиения области D на элементарные области Di (и, как следствие, стремление n к ∞ ) 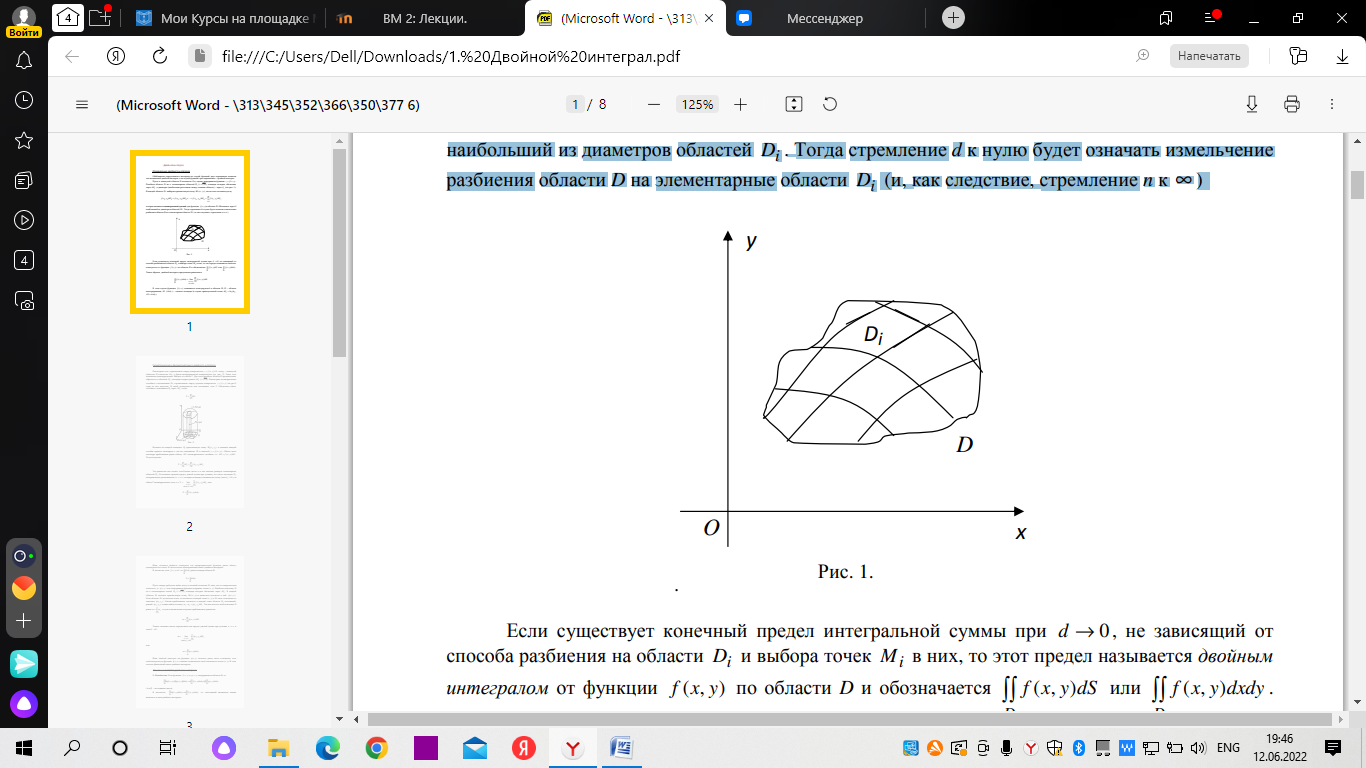 Если существует конечный предел интегральной суммы при d → 0, не зависящий от способа разбиения на области Di и выбора точек Mi в них, то этот предел называется двойным интегралом от функции f (x, y) по области D и обозначается 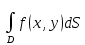 Таким образом, двойной интеграл определяется равенством 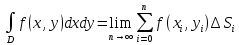 В этом случае функция f (x, y) называется интегрируемой в области D; D – область интегрирования, dS ( dxdy ) – элемент площади. Основные свойства двойного интеграла: 1. Линейность. Если функции f (x, y) и g(x, y) непрерывны на области D, то 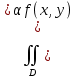 ± ±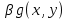 )dxdy= )dxdy=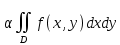 ± ±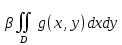 (β и α – постоянные числа) 2. Монотонность. Если функции f (x, y) и g(x, y) непрерывны на области D и всюду в этой области f (x, y) ≤ g(x, y) , то 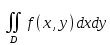 ≤ ≤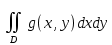 3. Теорема о среднем значении. Если функция f (x, y) непрерывна на области D, то существует точка 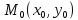 ∈ D такая, что ∈ D такая, что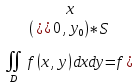 При этом значение 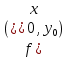 т.е. число 1/S т.е. число 1/S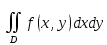 , называется интегральным средним значением функции f (x, y) в области D. , называется интегральным средним значением функции f (x, y) в области D.4. Аддитивность. Если область D представляется в виде объединения двух областей D1 и D2 без общих внутренних точек, то 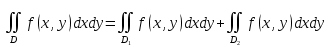 5. Для любой функции f (x, y) непрерывной на области D имеет место неравенство 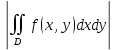 ≤ ≤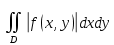 Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делается и при вычислении определенного интеграла), т.е. вводят новые переменные под знаком двойного интеграла. Определим преобразование независимых переменных x и y (замену переменных) как x = ϕ(u,v) и y = ψ(u,v) Если данные функции имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель 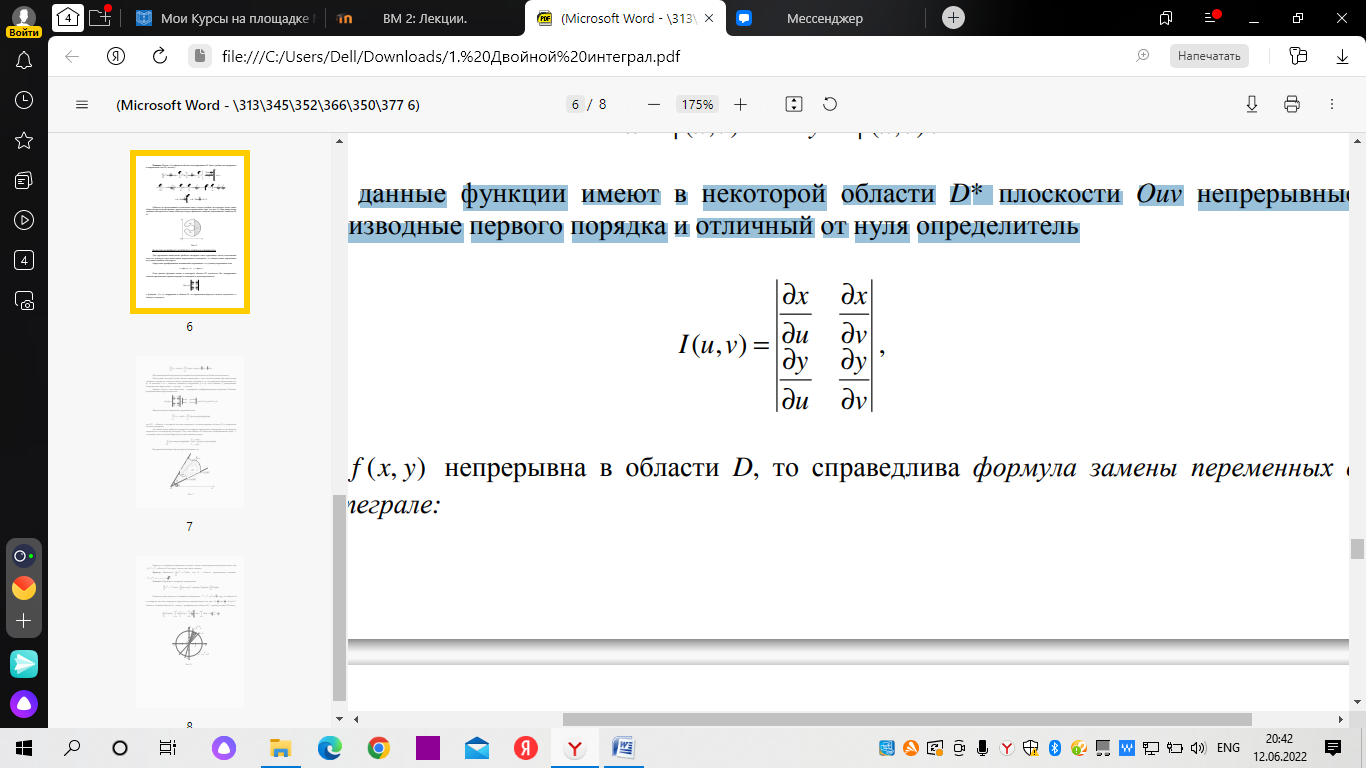 а функция f (x, y) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле: 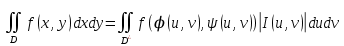 Функциональный определитель называется определителем Якоби или якобианом. Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат x и y полярными координатами ρ и ϕ. В качестве u и v возьмем полярные координаты ρ и ϕ. Они связаны с декартовыми координатами формулами x = ρcosϕ, y = ρsinϕ. Правые части в этих равенствах – непрерывно дифференцируемые функции. Якобиан преобразования определяется как 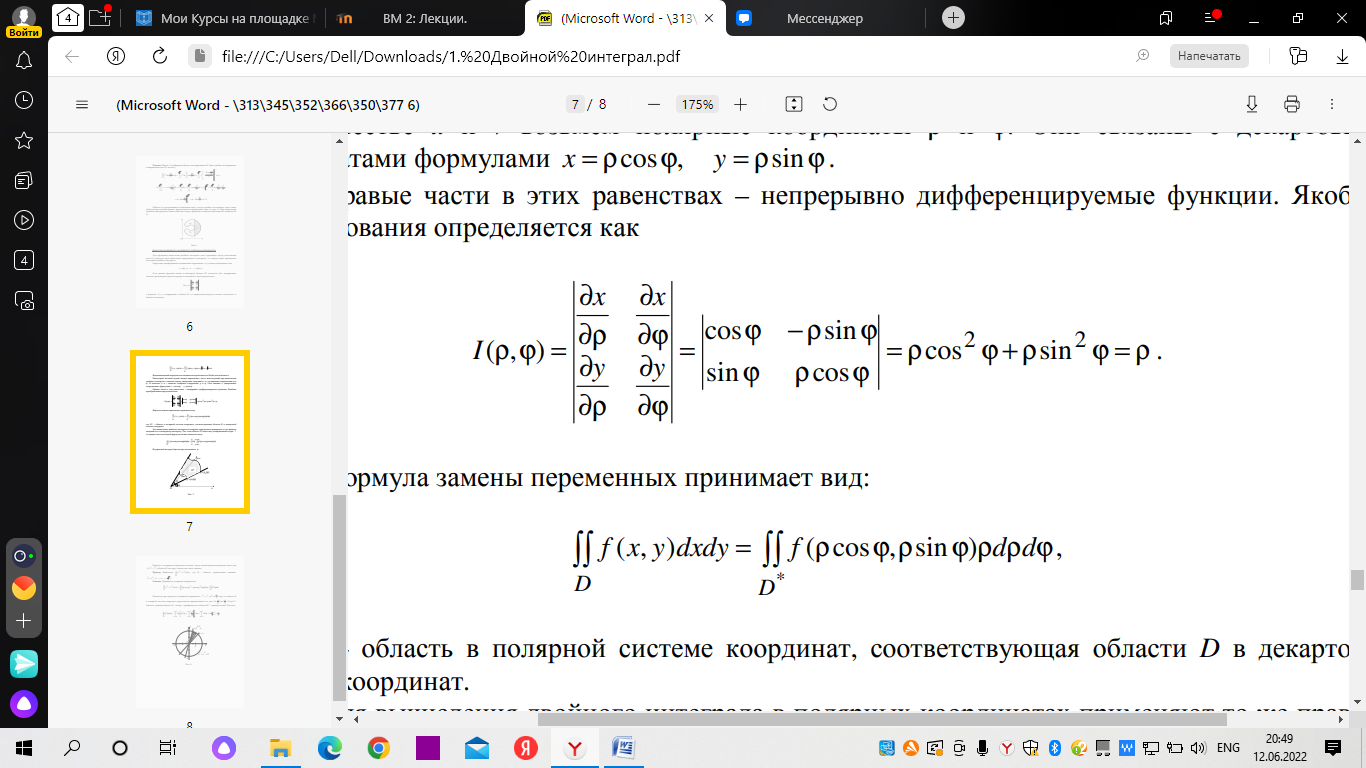 Формула замены переменных принимает вид: 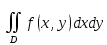 = =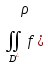 cos cos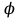 , ,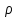 sin sin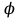 ) )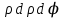 Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к повторному интегралу. 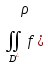 cos cos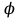 , ,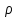 sin sin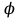 ) )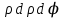 = =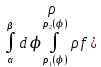 cos cos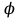 , ,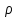 sin sin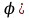 d d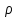 Внутренний интеграл берется при постоянном ϕ . Приложения двойного интеграла 1.Если D – ограниченная область плоскости Oxy, то ее площадь S вычисляется по формуле: S=S(D)= 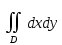 2.Пусть z = f (x, y) − неотрицательная, непрерывная функция в замкнутой области D. Если V – тело, ограниченное сверху поверхностью z = f (x, y), снизу – областью D, а сбоку – соответствующей цилиндрической поверхностью с образующей параллельной оси Oz и направляющей, совпадающей с границей области D, то объем этого тела равен S= 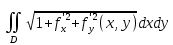 4. Предположим, что плоская пластина D имеет поверхностную плотность распределения масс γ(x, y) непрерывную в D. Тогда масса m этой пластины вычисляется по формуле m= 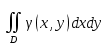 5. Статические моменты материальной пластины D с поверхностной плотностью γ(x, y) относительно координатных осей Ox, Oy и координаты ее центра тяжести соответственно вычисляются по формулам: 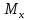 = =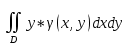 , , 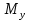 = =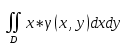 , ,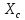 = =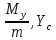 = =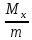 6. Моменты инерции плоской материальной пластины D с поверхностной плотностью γ(x, y) относительно координатных осей Ox, Oy и начала координат O(0,0) соответственно вычисляются по формулам: 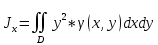 , ,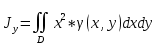 , ,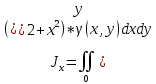 19. Понятие тройного интеграла. Основные определения. Свойства тройного интеграла. Замена переменных в тройном интеграле. Приложения тройного интеграла. Определение тройного интеграла аналогично определению двойного интеграла. Пусть в замкнутой области V пространства Oxyz определена и непрерывна функция трех переменных u = f (x, y,z). Разбив область V на n частей Vi (i = ,1 n ) и выбрав в каждой из них произвольную точку 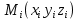 , составим интегральную сумму , составим интегральную сумму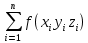 ∆ ∆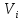 Если существует конечный предел интегральной суммы при d → 0 (здесь d – наибольший из диаметров областей Vi ), не зависящий от разбиения пространственной области на части Vi и выбора точек Mi в них, то этот предел называется тройным интегралом от функции f (x, y,z) по области V и обозначается 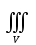 f (x,y,z)dxdydz . Таким образом, тройной интеграл определяется равенством f (x,y,z)dxdydz . Таким образом, тройной интеграл определяется равенством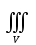 f (x,y,z)dxdydz= f (x,y,z)dxdydz=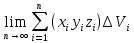 Свойства тройного интеграла аналогичны соответствующим свойствам определенного интеграла. 1. Линейность. Если функции f (x, y,z) и g(x, y,z) непрерывны в области V, то 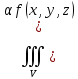 ± βg(x,y,z))dxdydz= ± βg(x,y,z))dxdydz=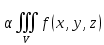 dxdydz ± dxdydz ± 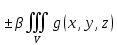 dxdydz, dxdydz, ( 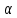 и β - постоянные числа) и β - постоянные числа)В частности, т.е. постоянный множитель можно выносить за знак двойного интеграла. 2. Монотонность. Если функции f (x, y,z) и g(x, y,z) непрерывны в области V и всюду в этой области f (x, y,z) ≤ g(x, y,z) , то 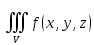 dxdydz ≤ dxdydz ≤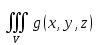 dxdydz dxdydz3. Теорема о среднем значении. Если функция f (x, y,z) непрерывна в области V, то существует точка M0 (x0 , y0 ,z0 ) ∈V такая, что 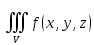 dxdydz= dxdydz=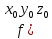 )*V )*V4. Аддитивность. Если область V представляется в виде объединения двух областей V1 и V2 без общих внутренних точек, то 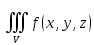 dxdydz= dxdydz=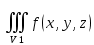 dxdydz+ dxdydz+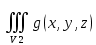 dxdydz dxdydz5. Для любой функции ( f (x, y,z)) непрерывной в области V имеет место неравенство 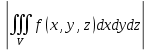 ≤ ≤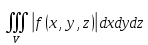 При вычислении тройного интеграла, как и двойного, часто применяется метод подстановки, т.е. совершается преобразование переменных. Пусть совершена подстановка x = ϕ(u,v,w), y = ψ(u, v, w), z = χ(u, v, w) . Если эти функции имеют в некоторой области 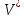 пространства Ouvw непрерывные частные производные и отличный от нуля определитель пространства Ouvw непрерывные частные производные и отличный от нуля определитель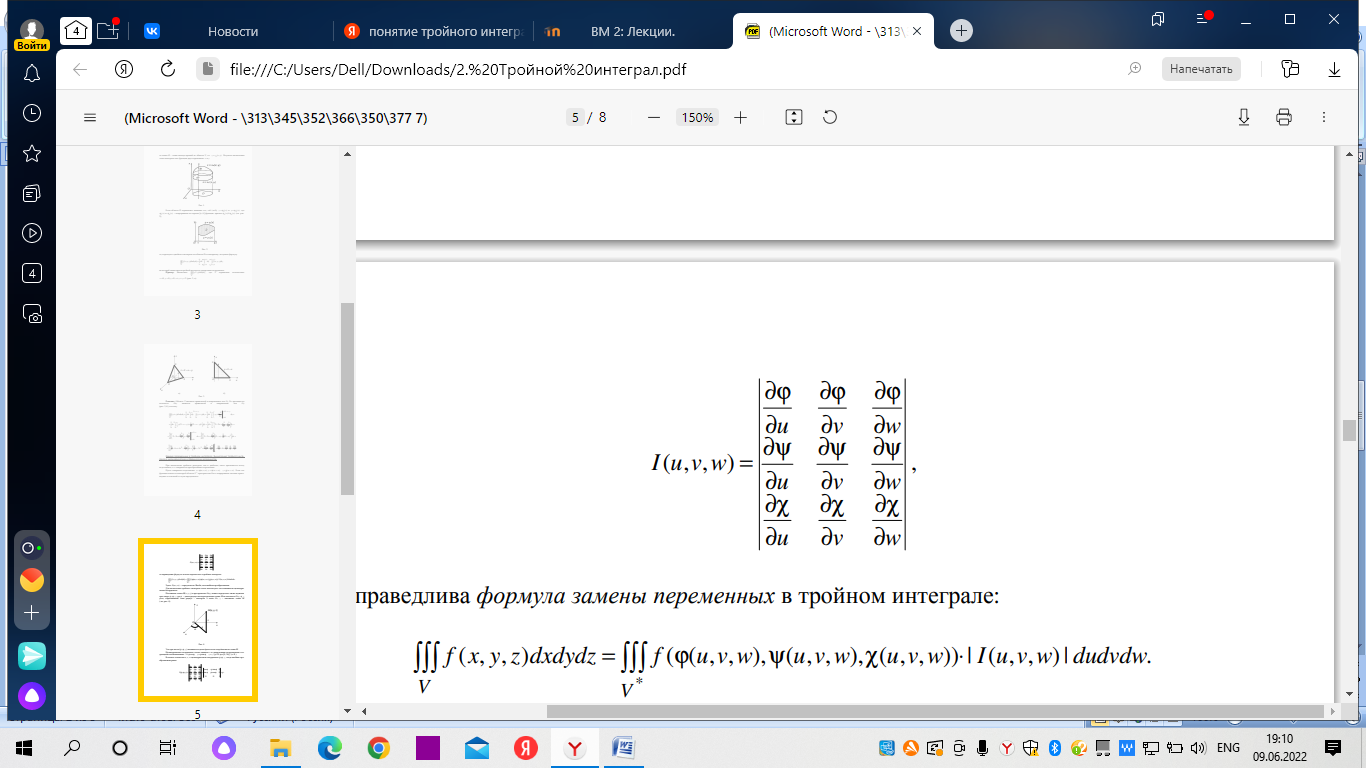 то справедлива формула замены переменных в тройном интеграле: 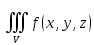 dxdydz= dxdydz=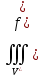 ϕ(u,v,w), ψ(u, v, w), χ(u, v, w))* ϕ(u,v,w), ψ(u, v, w), χ(u, v, w))*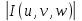 dudvdw dudvdwЗдесь I(u,v,w) − определитель Якоби, или якобиан преобразования. Далее приведем некоторые приложения тройных интегралов. 1.Объем V тела V находится по формуле: V= 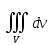 = = 2.Масса m тела V с заданной плотностью γ(x, y,z) , где функция γ(x, y,z) непрерывна, вычисляется по формуле: m= 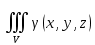 dxdydz dxdydz(физический смысл тройного интеграла). 3.Статические моменты M xy M xz M yz , , тела V относительно координатных плоскостей Oxy, Oxz, Oyz и координаты центра тяжести соответственно равны 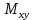 = =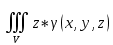 dxdydz, dxdydz, 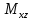 = =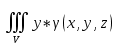 dxdydz, dxdydz,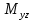 = =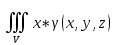 dxdydz, dxdydz,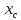 = =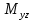 /m, /m, 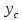 = =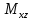 /m, /m, 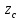 = =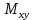 /m. /m.4. Моменты инерции Jxy Jxz Jyz тела V с плотностью γ(x, y,z) относительно координатных плоскостей Oxy, Oxz, Oyz вычисляются по формулам 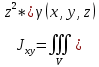 dxdydz, dxdydz, 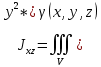 dxdydz, dxdydz, 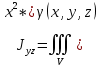 dxdydz. dxdydz.Моменты инерции 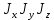 тела V с плотностью γ(x, y,z) относительно координатных осей Ox, Oy, Oz находятся по формулам тела V с плотностью γ(x, y,z) относительно координатных осей Ox, Oy, Oz находятся по формулам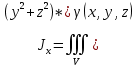 dxdydz, dxdydz, 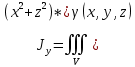 dxdydz, dxdydz, 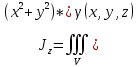 dxdydz. dxdydz.20. Понятие криволинейного интеграла первого рода. Свойства криволинейного интеграла первого рода. Способы вычисления. Пусть АВ – дуга гладкой кривой L и пусть задана функция f (M), непрерывная в каждой точке М дуги АВ. Разобьем произвольно дугу на n частей точками 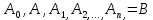 . Обозначим ∆li - длины частичных дуг . Обозначим ∆li - длины частичных дуг 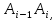 (i=1,2,…,n) и выберем на каждой из них по одной произвольной точке (i=1,2,…,n) и выберем на каждой из них по одной произвольной точке 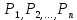 . Вычислим значение функции в этих точках и составим сумму . Вычислим значение функции в этих точках и составим суммуf( 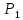 ) ∆ ) ∆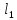 +f( +f(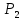 ) ∆ ) ∆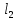 +…+f( +…+f(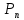 ) ∆ ) ∆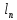 = =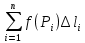 , ,которая называется интегральной суммой функции f(M) по дуге АВ. Очевидно, что данная сумма зависит от способа разбиения дуги АВ и от способа выбора точек Рi , поэтому можно составить бесчисленное множество различных интегральных сумм. Однако, при стремлении числа n к бесконечности и при стремлении наибольшей из длин частичных дуг max 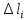 к нулю, все эти различные интегральные суммы стремятся к одному и тому же числу. к нулю, все эти различные интегральные суммы стремятся к одному и тому же числу.Итак, если при max 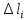 → 0 i l интегральная сумма → 0 i l интегральная сумма 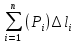 имеет определенный конечный предел, не зависящий от способа разбиения дуги АВ и от способа выбора точек Рi ∈ имеет определенный конечный предел, не зависящий от способа разбиения дуги АВ и от способа выбора точек Рi ∈ 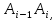 , то этот предел называется криволинейным интегралом 1-го рода от функции f(M) по дуге АВ и обозначается , то этот предел называется криволинейным интегралом 1-го рода от функции f(M) по дуге АВ и обозначается 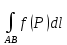 Основные свойства : 1) 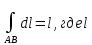 - длина дуги АВ. - длина дуги АВ.2) 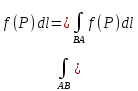 , то есть данный интеграл не зависит от ориентации кривой. , то есть данный интеграл не зависит от ориентации кривой.3) 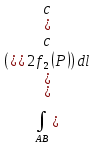 = = 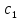 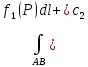 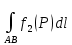 , где , где 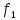 (P), (P), 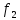 (P), функции, интегрируемые на кривой L, c1 c2 – произвольные числа (P), функции, интегрируемые на кривой L, c1 c2 – произвольные числа4) 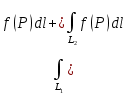 = = 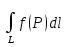 , где L = L1 ⊕ L2 , где L = L1 ⊕ L2Вычисление криволинейного интеграла 1-го рода: Пусть кривая L на плоскости Oxy задана параметрическими уравнениями L : x = x(t), y = y(t), α ≤ t ≤ β , где x(t), y(t) непрерывно дифференцируемые функции. Имеет место следующая теорема. Теорема 1. Если гладкая кривая L задана параметрическими уравнениями x= x(t), y=y(t), ), α ≤ t ≤ β и функция f(x,y) является непрерывной на L, то существует криволинейный интеграл 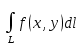 , причем , причем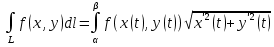 dt dtОтметим, что если кривая L задана в трехмерном пространстве, то 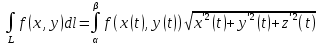 dt dtЕсли кривая L задана уравнением y = y(x), a ≤ x ≤ b , где y(x) непрерывно дифференцируемая функция на отрезке [a, b], то следует 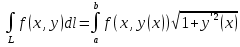 dx dxПусть кривая L задана на плоскости полярным уравнением L: r = r (ϕ), 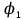 ≤ ϕ ≤ ≤ ϕ ≤ 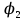 где функция r (ϕ) непрерывно дифференцируема на отрезке [ где функция r (ϕ) непрерывно дифференцируема на отрезке [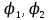 ] . Тогда можно получить ] . Тогда можно получить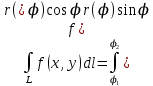 ) )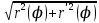 dϕ dϕДействительно, принимая за параметр t угол ϕ и с учетом формул x= 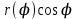 , y= , y=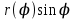 , найдем , найдем 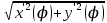 dϕ= dϕ= 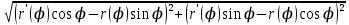 d d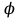 = =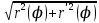 dϕ dϕ |
