Функция. Функция х равна наибольшему целому числу, не превосходящему х (х любое действительное число). Например, 2
 Скачать 47.83 Kb.
|
      Функция [х] равна наибольшему целому числу, не превосходящему х (х – любое действительное число). Например, 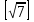 = 2,  = -4,  Функция [x] имеет «точки разрыва»: при целых значениях х она «изменяется скачком» 321 у На рис.2 дан график этой функции, причем левый конец каждый из горизонтальных отрезков принадлежит (жирные точки), а правый – не принадлежит. -2 -2 -1 1 2 3 4 х Попробуйте доказать, что если каноническое разложение числа n! есть n! =    … , то α = +  +  +…Аналогичные формулы имеют место для β, γ, σ. Зная это, легко определить, например, сколькими нулями оканчивается это число 100! Действительно, пусть 100!=    … . Тогда α = 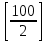 +  + + + +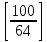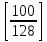…=97 и γ =  + +…=24Следовательно, 100! Делится на  , т.е. оканчивается двадцатью четырьмя нулями.Приложение Как известно, n! = 1·2·3·4·5·…·(n-2)·(n-1) ·n. (**) Если перебирать по порядку эти множители, то через каждые  «шагов» будут встречаться множители, кратные простому числу ; число их равно  , но из них множителей делятся на  , – делятся на  и т.д.Следовательно, число множителей в равенстве (**), в состав которых множитель  входит ровно один, два, три и т.д. раза, соответственно равно числам: -, -,- и т.д.Поэтому α= -+2· +3 +… = +++… |