курс. Курсовая работа ПЗ исправила. Гарифуллина Н. А
 Скачать 2.25 Mb.
|
         Гарифуллина Н.А. Фамилия И.О. ПАД-124С 1306.3013XX.000 ПЗ Информатики Информатика и языки программирования Уфа – Методы решения нелинейных уравнений Содержание 1Математическое описание метода решения задачи 4 1.1Постановка задачи поиска корней уравнения 4 1.2Обзор методов решения задачи 5 1.1Описание выбранного метода решения задачи 6 2Разработка алгоритма решения задачи 16 2.1Постановка задачи 16 2.2Описание входных и выходных данных 16 2.3Блок схема алгоритма 16 2.4Фрагменты исходных текстов, отвечающие за решение задачи 16 3Экспериментальная проверка работоспособности ПО 17 3.1Экранные формы выполненного разработанным ПО расчета 17 3.2Поиск решения задачи с помощью MS Excel 17 3.3Поиск решения задачи с помощью системы компьютерной математики Scilab 19 3.4Оценка погрешности решения задачи 20 Целью выполнения курсовой работы по дисциплине «Информатика и языки программирования» специальности 24.05.02 Проектирование авиационных и ракетных двигателей, является: закрепление и углубление знаний, формирование умений и практических навыков применения средств разработки прикладного программного обеспечения для решения практических задач области проектирования и разработки авиационных двигателей на примере задачи поиска решения нелинейных уравнений. Задачами курсовой работы являются: изучение метода решения нелинейных уравнений; разработка алгоритма метода решения задачи поиска корней нелинейных уравнений; реализация алгоритма в виде прикладной программы для ЭВМ на языке программирования Си(Си++); выполнение экспериментальной проверки работоспособности разработанного программного обеспечения и сопоставление получаемой точности с решением в математическом пакете.
На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами. В зависимости от сложности задачи, заданной точности, применяемого метода может потребоваться огромное количество действий, и здесь без быстродействующего компьютера не обойтись. Решение, полученное численным методом, обычно является приближенным, т. е. содержит некоторую погрешность. Источниками погрешности приближенного решения задачи являются: погрешность метода решения; погрешности округлений в действиях над числами. ДАЛЕЕ ПРЕДСТАВЛЕННЫЙ ТЕКТ ПЕРЕНАБРАТЬ ИЛИ НАЙТИ ПОДОБНОЕ В ИНТЕРНЕТЕ (например https://studfile.net/preview/3064885/ , https://prog-cpp.ru/digital-find/ )  
 Ссылка на книгу в этой картинке: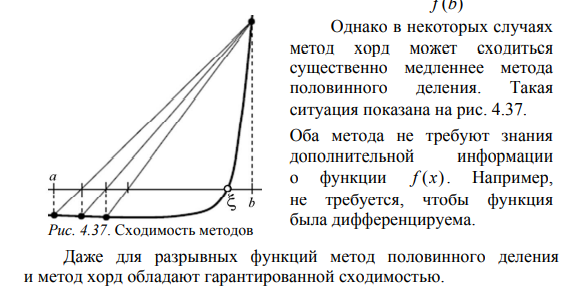    
Рассматривается только Ваш метод решения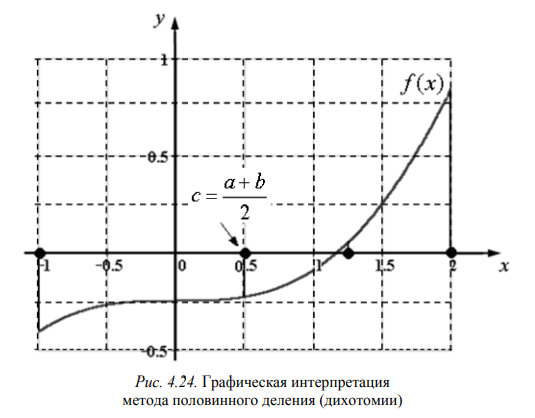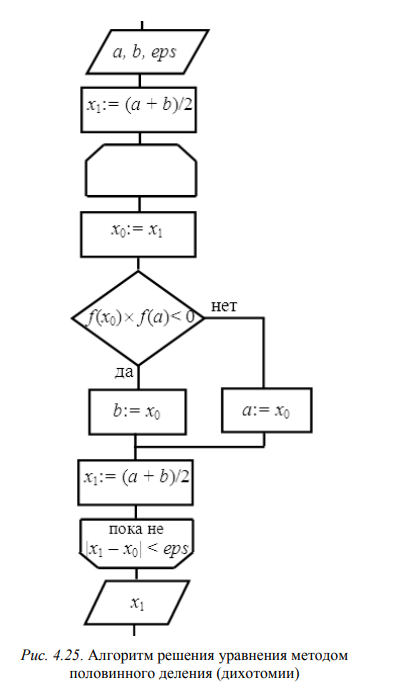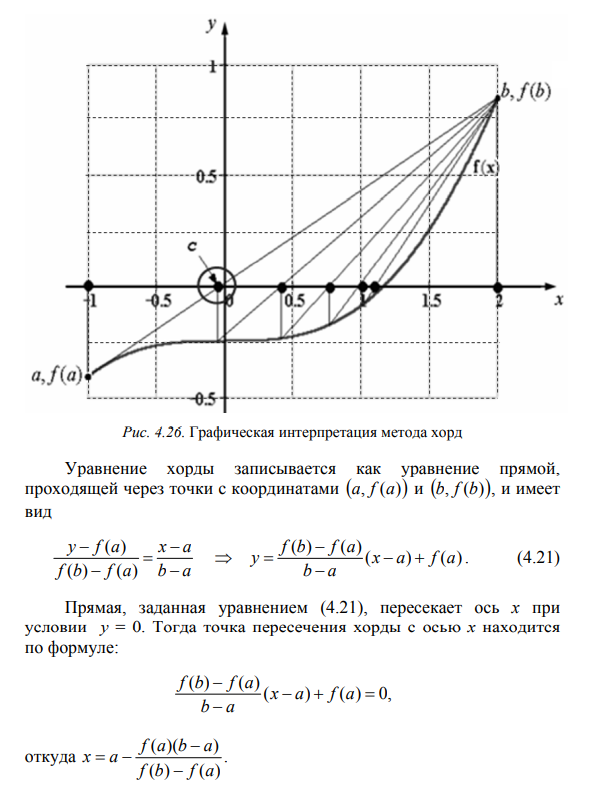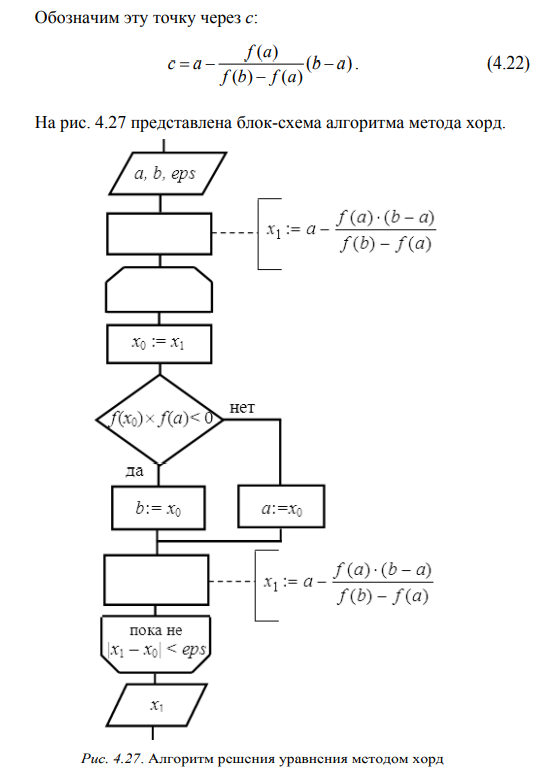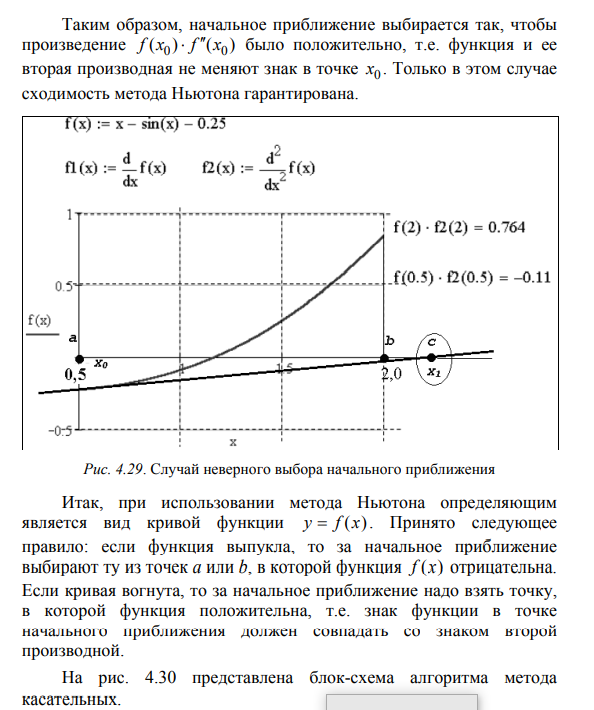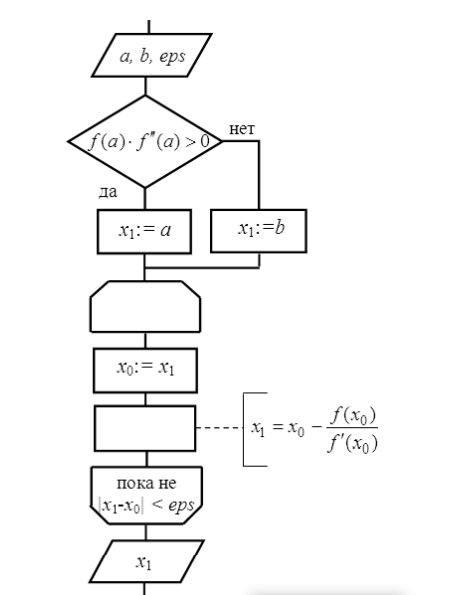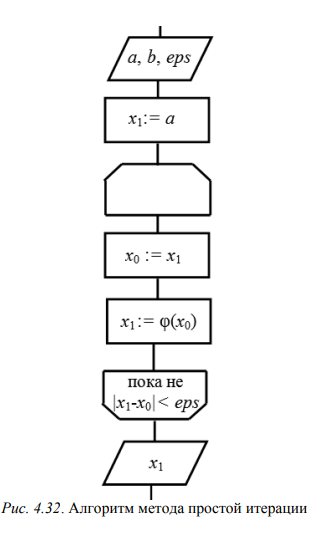                 
1. Разработать блок-схему алгоритма поиска корней нелинейного уравнения 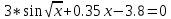 на отрезке [2;3] методом итераций. Интервал поиска корней уравнения и точность результата задается с клавиатуры.2. Выполнить кодирование разработанного алгоритма на языке С/С++. 3. Проверить работоспособность и выполнить оценку погрешности решения реализованного алгоритма путем сравнения результата вычислений с результатом решения, полученного в математическом пакете Scilab и в табличном процессоре MS Excel. 4. Разработать и реализовать алгоритм отображения процесса последовательного уточнения корней в текстовом режиме. 5. Разработать и реализовать алгоритм отображения процесса последовательного уточнения корней в графическом режиме.
Описать
Добавить блок-схему Вашего алгоритма
for i in range(len(string)): for j in range(len(b)): if (string[i] == b[j]):
k = k + 1
Привести несколько скриншотов при различных начальных условиях (с разной точностью) 
МОЖНО БОЛЕЕ КРАТКО, но с формулами и без, подбор параметра и поиск решения. Задаём значения аргумента. Для этого вводим в ячейку А4 левую границу диапазона – 1,5, а в ячейку А5 вводим число, равное левой границе диапазона плюс шаг 0,05. Выделяем обе ячейки и с помощью маркера автозаполнения в виде знака «+» копируем выделенные ячейки вниз, пока не появится правая граница диапазона – 2. Задаём в ячейке В4 формулу для вычисления значений функции. Для этого в строке ввода формул нажимаем клавишу «=» (равно) и начинаем набирать формулу, указывая в качестве аргументов ссылки на ячейки листа, где эти аргументы находятся: =SIN(2^((A4-1)/(A4+1)))-2*COS(2^(2*A4-1)). После набора формулы выделяем ячейку, где она находится, и маркером автозаполнения копируем формулу на весь диапазон значения аргумента. Строим график функции. Для этого выделяем мышкой диапазон ячеек, где находятся значения аргумента и функции, и вызываем Мастер диаграмм. Тип диаграммы на 1-ом шаге мастера указываем «Точечная с гладкими кривыми и маркерами». Анализируем построенный график. Определяем, сколько корней имеет уравнение, в левой части которого стоит функция, на заданном диапазоне. Имеем два пересечения с осью Ох, поэтому будет два решения уравнения у=0. Найдём (уточним корень). Для уточнения корня используем команду меню Данные → Анализ «что если» → Подбор параметра. Корень можно находить с помощью Данные → Поиск решения.  . График функции. Корни 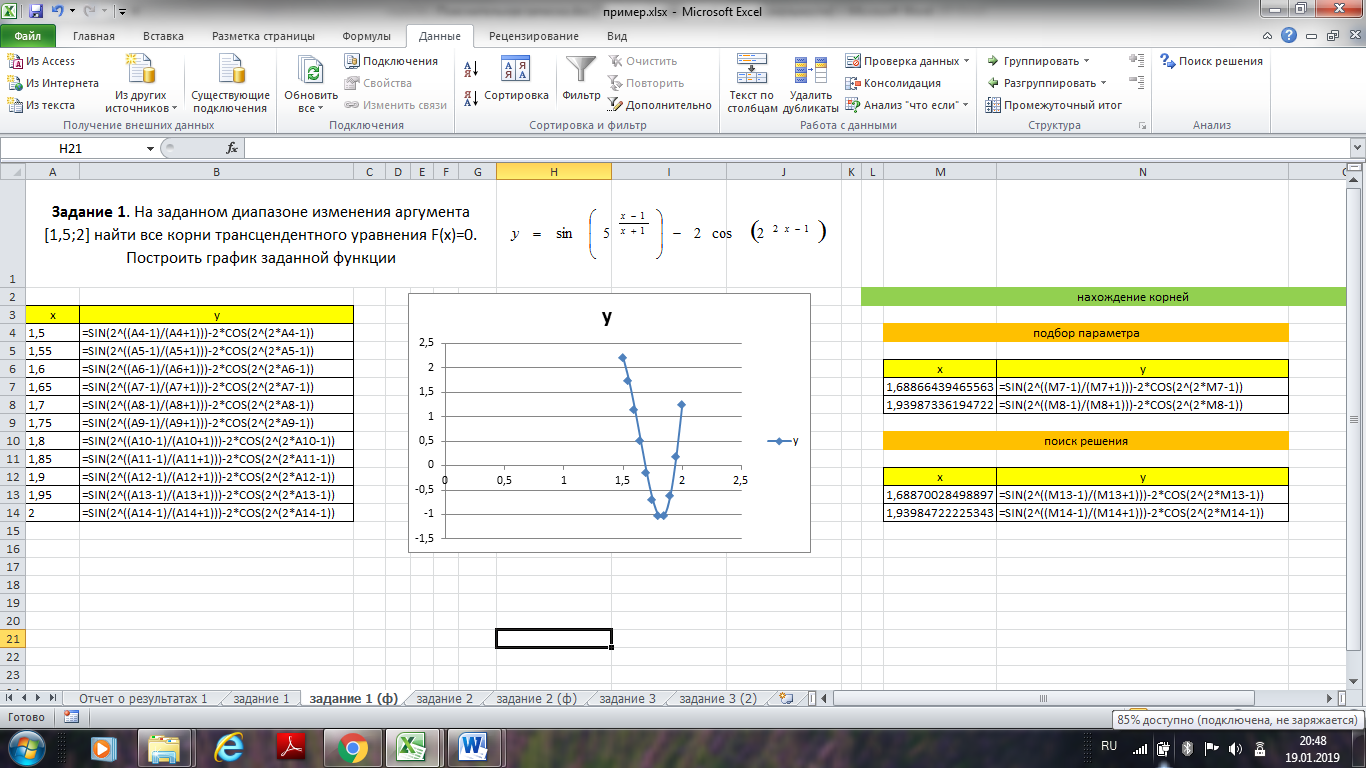 . Формулы.
Для выполнения расчетов в системе компьютерной математики Scilab, сначала с помощью конструкции function … endfunction определяем вид функции, задаем вектор диапазона значений аргумента х, вычисляем вектор значений функции у и строим график функции. На втором этапе по графику функции определяем начальные приближения корней х1=1.7, х2=1.9. После чего с помощью функции fsolve уточняем корни. 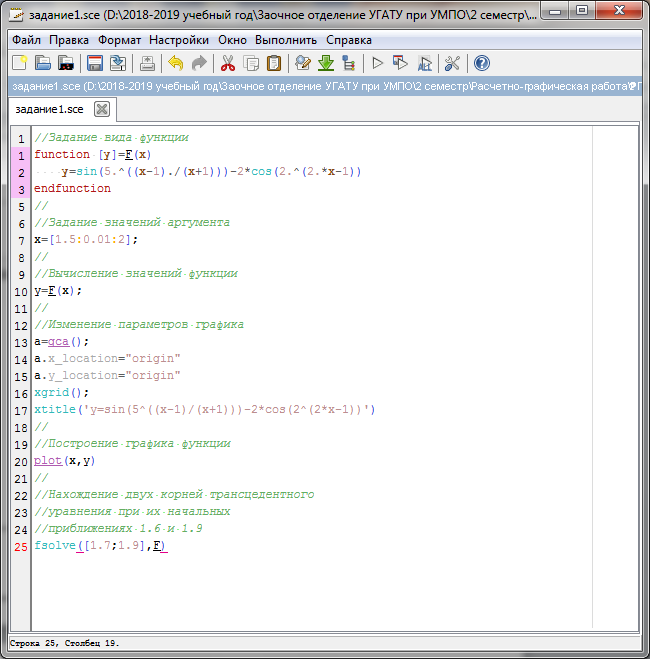 . Файл-сценарий нахождения корней трансцендентного уравнения 
Сравнить решение программированием с результатами в Excel и Scilab Заключение В результате выполнения курсовой работы была разработана математическая модель и алгоритм решения нелинейного уравнения 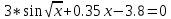на отрезке [2;3] методом итераций. По разработанному алгоритму реализована программа и комплект проверочных заданий для оценки корректности ее работы. Результаты оценки показали, что программа находит решения с точностью XXX, относительная погрешность не превышает XXX%.Таким образом, можно сделать вывод о том, что применяемый способ/метод/алгоритм и т.п. можно применять для решения поставленной задачи. В качестве программного инструментального средства для решения задачи был применен …. По факту выполнения заданий можно сделать вывод, что данный инструмент эффективен/неэффективен для решения подобного типа задач и может/не может использоваться на практике. Список литературы Если использовали материал из указаний Карчевской, то добавляем его в список литературы, если другое – указываем что именно. Керниган Б., Ритчи Д. Язык программирования С / The C Programming Language. М.: Вильямс, 2017 – 292 c. Сикорд Роберт С. Эффективный C. Профессиональное программирование. – СПб.: Питер, 2022. – 304 с.: ил. – (Серия «Библиотека программиста»). Прата, Стивен. Язык программирования С. Лекции и упражнения, 6-е изд. : Пер. с англ. – М. : ООО “И.Д. Вильямс”, 2015. – 928 с. ГОСТ 2.105-2019. Общие требования к текстовым документам. М., 2021. 31 с. Карчевская, М. П. Основы алгоритмизации инженерных задач [Электронный ресурс]: [учебное пособие для студентов специальностей 27.05.01 "Специальные организационно-технические системы"; 10.05.05 "Безопасность информационных технологий в правоохранительной сфере"; 09.05.01 "Применение и эксплуатация автоматизированных систем специального назначения"] / М. П. Карчевская, О. Л. Рамбургер; Уфимский государственный авиационный технический университет (УГАТУ). — Электронные текстовые данные (1 файл: 6,06 МБ). — Уфа: УГАТУ, 2019. — Электронная версия печатной публикации. — Заглавие с титул. экрана. — Доступ из сети Интернет по логину и паролю. Анонимный доступ из корпоративной сети УГАТУ. — Систем. требования: Adobe Reader. — URL:http://e-library.ufa-rb.ru/dl/lib_net_r/Karchevskaya_M_P_Osn_algor_inzh_zad_2019.pdf . Приложения Полный текст программы |